马敏耀，刘 卓，徐 艺，吴 恋

（1.贵州师范学院数学与大数据学院，贵阳 550018；2.贵州师范学院网络空间安全重点实验室，贵阳 550018）

0 引言

安全多方计算技术常用来解决各种隐私保护科学计算问题，研究如何使互不信任的多个参与方在不借助任何第三方的情况下实现保护隐私的协同计算。只有两个参与方的安全多方计算常称为安全两方计算，即参与方A1和A2分别拥有自己的秘密输入x1和x2，在不借助任何第三方的情况下联合计算某个二元函数（y1，y2）=f（x1，x2），协议结束后至少满足两个特性：1）正确性，即参与方Ai得到本方的正确输出yi；2）安全性，即任何一方的输入信息都未泄露给其他人。Yao 于1982年在文献［1］中最先提出安全多方计算的思想。随后，安全多方计算受到广泛的研究，其中文献［2-4］研究安全多方计算的可行性问题，即研究具体安全模型下安全多方计算协议的存在性问题，以及通用安全多方计算协议的构造问题，即构造能计算任意可计算函数的通用安全多方计算协议。一般而言，通用安全多方计算协议的执行效率不高，因此需要针对具体的安全多方计算问题研究个性化的解决方案。例如文献［5］研究隐私保护线性代数计算问题，文献［6］研究隐私保护脱氧核糖核酸（DeoxyriboNucleic Acid，DNA）序列汉明距离计算问题，文献［7-9］研究百万富翁问题等安全数值计算问题，文献［8-10］研究安全多方量子计算问题，文献［10-15］研究安全多方集合计算问题，文献［16］在安全多方计算模型下研究基于多方数据集的隐私保护机器学习问题，文献［17-19］研究保密区间计算问题。

本文提出一种新的安全两方计算问题，即隐私保护整数区间位置关系判定问题，研究如何让拥有整数区间的两个用户，在保护输入隐私的前提下，准确地判断出二者的整数区间的位置关系，其中整数区间是指左右端点都是整数，由区间的左右端点及介于它们之间的所有整数构成的集合。例如整数区间［3，6］表示集合｛3，4，5，6｝。整数区间的位置关系是指两个整数区间在数轴上的位置的相对关系，本文将定义整数区间的6 种位置关系，在设计整数区间位置关系判定协议时，需要保证两个参与方能够正确地判断出彼此持有的整数区间的位置关系属于6 种关系中的哪一种，同时保证各自的区间信息未被泄露。

隐私保护整数区间位置关系判定问题有着重要的应用背景，下面是几个例子：在商务上，利益方之间有时需要根据彼此的价格区间的位置关系来制定进一步的合作计划，而各自的价格区间都是高度利益相关的，他们需要在隐私保护的前提下判断出彼此价格区间的位置关系；爆发大规模的疫情可能会导致某类商品出现大幅的价格波动，不同的机构根据自有模型预测出不同的价格区间，在保护隐私的前提下判断出这些价格区间的位置关系有助于相关问题的决策，且能保护各方的隐私；源于某种动机，Bob 需要判断自己持有的某个时间区间［t1，t2］与Alice访问某网络服务的时间区间［T1，T2］（记录保存在服务器S端）之间的位置关系，B和S在保护隐私的前提下判断此位置关系，既解决了面临的问题，又保护了各方的隐私。

文献［17-20］在隐私保护区间计算方面作了一些研究，但主要研究元素是否属于区间的判定问题。特别地，文献［19］的部分工作和文献［20］都研究了整数点是否属于整数区间的隐私保护判定问题。目前尚未发现有关隐私保护区间位置关系判定问题的研究工作，而前人关于隐私保护区间计算方面的研究成果，尚不能直接扩展为解决该问题的方案，因此本文对隐私保护区间位置关系判定问题开展研究。

本文取得的主要工作如下：

1）定义了整数区间的6 种位置关系，并给出整数区间的一种0-1 编码方案，然后证明了两个整数区间位置关系的判定定理，从而将整数区间位置判定问题转化为0-1 串之间的汉明重量比较问题。

2）在半诚实攻击者模型［21］下，基于给出的判定规则，借助Goldwasser-Micali 加密体制［22］，主要是利用其异或同态性和概率加密特性，设计了一个整数区间位置关系判定协议，给出了基于模拟器的安全性证明，并对协议的性能进行了分析和说明。

1 知识准备

1.1 Goldwasser-Micali加密体制

N是正整数，定义={a∈ZN：gcd(a，N)=1}。称a∈是模N的二次剩余，若x2≡amodN对某个x∈ZN成立；否则称a为模N的二次非剩余。判断a是否是模N的二次剩余的问题称为模N的二次剩余问题，当未知N的素因数分解时该问题是困难的，已知N的素因数分解时该问题是容易的。

Goldwasser-Micali 加密体制［22］是基于模N的二次剩余问题困难性的公钥加密体制，其密钥生成算法、加密算法和解密算法描述如下。

未知私钥（即未知大整数N的因数分解）时，模N的二次剩余问题是困难的，故解密是困难的；拥有私钥（即知道N的因数分解）时，模N的二次剩余问题是容易的，故解密是容易的。该密码系统具有如下特性。

1）概率加密特性：每次加密都有随机数r参与运算。

2）异或同态性：Epk(x1)和Epk(x2)分别是x1和x2的密文，则(Epk(x1)⋅Epk(x2))modN是x1⊕x2的密文，即(Epk(x1)⋅Epk(x2))modN=Epk(x1⊕x2)。

1.2 半诚实攻击模型下的安全两方计算模型

在研究安全多方计算问题时，半诚实模型和恶意模型是考虑得最多的两种攻击者模型。文献［21］基于比特承诺和零知识证明理论设计了一个编译器，能够将半诚实攻击者模型下安全计算函数f的一个多方计算协议编译成在恶意攻击者模型下安全计算f的另一个多方协议。因此在处理具体的安全多方计算问题时，人们往往先探索半诚实攻击者模型下的解决方案，再进一步构建恶意攻击者模型下的解决方案。鉴于此，本文在半诚实攻击者模型下研究隐私保护整数区间位置判定问题，恶意攻击者模型下的研究工作作为下一步工作。

下面给出半诚实攻击模型下的安全两方计算模型［21］，它是本文协议安全性证明的理论根据。直观地讲，在半诚实攻击模型下，假定协议的每个参与方都严格地遵循协议步骤，但允许它们记录自己在执行协议过程中的中间信息，以此去推测对方的秘密输入。令f：{0，1}*×{0，1}*→{0，1}*×{0，1}*，其中f(X，Y)=(f1(X，X)，f2(X，X))是一个二元概率多项式时间函数，记Π是计算f的一个两方协议。两个参与方P1和P2分别以X和Y为输入，协议Π 执行结束后，参与方P1的，参与方P2的view为，其中ri表示Pi的内部随机带的输出,表示Pi收到的第j条信息。记Pi的output为。对函数f=(f1，f2)，称Π 是半诚实攻击模型下计算f的安全两方计算协议［21］，若存在概率多项式时间算法S1和S2，分别使得下面两个关系式成立，其中表示随机变量簇是计算不可区分的：

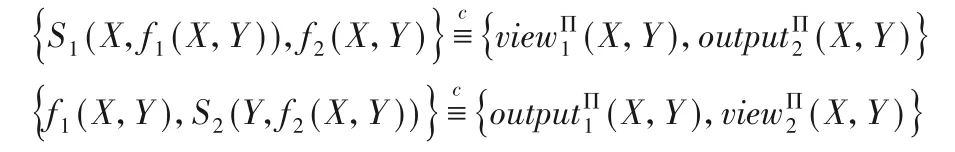
1.3 问题定义

设y1和y2（y1＜y2）是两整数，整数区间[y1，y2]是指由y1和y2以及它们之间的所有整数构成的集合，即是集合{y1，y1+1，y1+2，…，y1+(y2-y1)}，含y2-y1+1 个 连 续整数。

定义1对点整数x和整数区间[y1，y2]，定义如下两种位置关系，其中“⇔”表示充分必要条件（下同）：

1）（小于关系≺）：x≺[y1，y2]⇔x＜y1；

2）（大于关系≻）：x≻[y1，y2]⇔x＞y2。

从数轴上看，x≺[y1，y2]相当于点x在区间[y1，y2]的左侧，x≻[y1，y2]相当于点x在区间[y1，y2]的右侧。可见，点x和区间[y1，y2]共有x∈[y1，y2]，x≺[y1，y2]和x≻[y1，y2]三种可能的位置关系（如图1所示）。

图1 整数点和整数区间的三种位置关系Fig.1 Three relationships between integer and integer-interval

定义2定义整数区间[x1，x2]和[y1，y2]的如下6 种位置关系（如图2所示），其中“∧”表示逻辑关系“与”：

图2 整数区间的6种位置关系Fig.2 Six relationships between integer-intervals

需要强调的是关系[y1，y2]⊂[x1，x2]要求x1＜y1且y2＜x2，这不同于集合之间的真包含关系“⊂”。例如区间位置关系[3，5]⊂[3，7]并不成立，因为不满足条件6），但作为集合关系{3，4，5}⊂{3，4，5，6，7}是成立的。从数轴上看，关系1）表示区间[x1，x2]在[y1，y2]的左侧，二者没有相交；关系2）表示[x1，x2]的右端点x2向右滑动满足x2∈[y1，y2]，而左端点x1继续保持位于[y1，y2]的左侧；关系3）表示[x1，x2]的左端点x1向右滑动满足x1∈[y1，y2]，而右端点x2继续保持位于[y1，y2]的内部，即x2∈[y1，y2]；关系4）表示[x1，x2]的右端点x2继续向右滑动至[y1，y2]的右侧，而左端点x1继续保持位于[y1，y2]的内部；关系5）表示[x1，x2]的左端点x1继续向右滑动至[y1，y2]的右侧，此时区间[x1，x2]在[y1，y2]的右侧，二者没有相交；而关系6）则表示[x1，x2]的左端点x1位于[y1，y2]的左侧而右端点x2位于[y1，y2]的右侧。

下文中，全集U={u1，u2，…，un}都指由某n个连续整数构成的公开集合，即形如{u1，u1+1，…，u1+(n-1)}⊆Z，这意味着ui＜uj⇔i＜j，即较小的下标对应较小的数值。例如集合U=｛1，2，3，4，5，6，7，8，9，10，11，12｝可作为全集。

定义3隐私保护整数区间位置判定问题。全集U={u1，u2，…，un}是由n个连续整数构成的公开集合，用户Alice和Bob 分别拥有整数区间[x1，x2]⊆U和[y1，y2]⊆U，隐私保护整数区间位置判定问题即是在保证各自的区间信息不被泄露的情况下，Alice 和Bob 如何正确地判断出整数区间[x1，x2]和[y1，y2]的位置关系，即属于定义2中的何种情形。

2 编码规则和判定定理

2.1 编码规则

全集U={u1，u2，…，un}是由n个连续整数构成的集合，Alice 拥有整数区间[x1，x2]⊆U，Bob 拥有整数区间[y1，y2]⊆U。下面分别定义Alice 和Bob 的0-1 编码规则，将区间[x1，x2]和[y1，y2]编码成两个n长的0-1串。

1）Alice 将区间[x1，x2]编码成长度为n的两个0-1编码a=a1a2…an和d=d1d2…dn，满足：

①若ui=x1则ai=1，否则ai=0；

②若ui=x2则di=1，否则di=0。

2）Bob 将区间[y1，y2]编码成长度为n的两个0-1 编码b=b1b2…bn和c=c1c2…cn，满足：

①若ui≥y1则bi=1，否则bi=0；

②若ui＞y2则ci=1，否则ci=0。

需要强调的是：在Bob构造0-1编码c的过程中是用“＞”而不是“≥”。特别，当y2=un（即取全集U中的最大值）时，c=00…0。下面通过实例1对0-1编码规则进行辅助说明。

实 例1 设U={1，2，3，4，5，6，7，8，9，10，11，12}，Alice和Bob 分别拥有区间[x1，x2]=[5，7]和[y1，y2]=[4，8]，Alice得到两个0-1 串a=000010000000 和d=000000100000，Bob 得到两个0-1串b=000111111111和c=000000001111。

2.2 判定定理

本节将根据上述0-1编码规则，分别给出整数区间的6种位置关系的充分必要条件，这是本文协议的主要理论基础。下面先通过引理1 给出整数点与整数区间3 种位置关系的充分必要条件，然后基于此，通过定理1 给出整数区间位置关系的充分必要条件。

定义4比特串s=s1s2…sm∈{0，1}m中所含“1”的个数称为s的重量，记为N(s，1)，即N(s，1)=

例如：令s=001110010，则N(s，1)=4。

引理1全集U={u1，u2，…，un}是由n个连续整数构成的集合，对整数点x∈U和整数区间[y1，y2]⊆U，将它们分别按如下规则进行0-1 编码，得到长度为n的0-1 串a=a1a2…an，b=b1b2…bn和c=c1c2…cn：1）若ui=x则ai=1，否则ai=0；2）若ui≥y1则bi=1，否则bi=0；若ui＞y2则ci=1，否则ci=0。则下列关系成立（其中“||”表 示0-1 串的级联，如x=100，y=1100，则x||y=1001100）：

证明 由于a，b，c都是等长的，则下列等式成立：

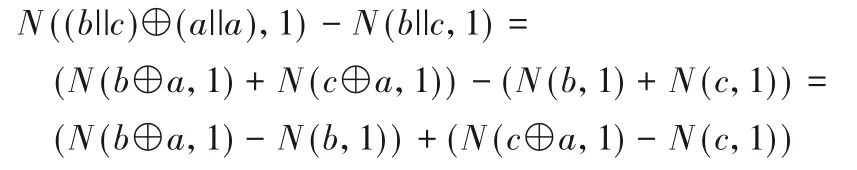
先证明关系1）成立。假设x∈[y1，y2]，即y1≤x≤y2。故uk≤ui≤uj-1。根据全集U的定义规则，下标小意味着对应的数值也小，即k≤i≤j-1。可得N(b⊕a，1)-N(b，1)=-1和N(c⊕a，1)-N(b，1)=1。故有：

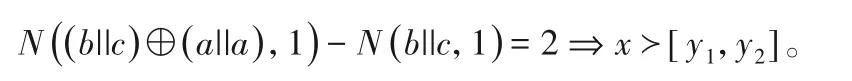
下面基于引理1，给出整数区间位置关系的判定定理。

定理1 判定定理。全集U是由n个连续整数构成的集合，整数区间[x1，x2]和[y1，y2]是U的两个子区间。设a，b，c，d是区间[x1，x2]和[y1，y2]按如上0-1 编码规则进行编码后得到的四个0-1串，而a||a，d||d和b||c是按照0-1串的级联得到的3个2n长的0-1串。记：

根据定理1 的结论，要判断区间[x1，x2]和[y1，y2]的位置关系，只需求出数对(L1，L2)的值即可。在0-1 串a，b，c，d中，Bob拥有b和c，因此他能本地计算N(b||c，1)。由于

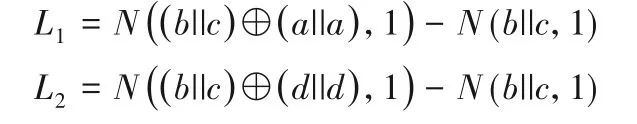
因此，如果能够在保护隐私的前提下，让Bob 得到N((b||c)⊕(a||a)，1)和N((b||c)⊕(d||d)，1)，他就能计算出数对(L1，L2)的值，从而获知[x1，x2]和[y1，y2]的位置关系，然后把结果告知Alice。为此，由于Bob 拥有(b||c)，Alice 拥有a||a和d||d。自然的想法是双方在保护隐私的情况下，执行一系列协议步骤让Bob 得到N((b||c)⊕(a||a)，1)，然后再重复执行类似步骤，让Bob 得到N((b||c)⊕(d||d)，1)。但这样做带来的问题是协议的轮复杂度较高，彼此收发消息的数量增加，会对协议的性能产生负面影响。因此，本文在设计协议时充分考虑到这一点，在保护隐私的前提下，让Bob 一次性得到(L1，L2)的值，将协议的轮复杂度降低了一半。

下面通过实例2对定理1给出的判定规则进行辅助说明。

实例2 设U={1，2，3，4，5，6，7，8，9，10，11，12}，对两个区间[x1，x2]=[3，7]和[y1，y2]=[6，10]，Alice 得到两个0-1 串a=001000000000 和d=000000100000，Bob 得到两个0-1 串b=000001111111和c=000000000011。易见N(b||c，1)=9。

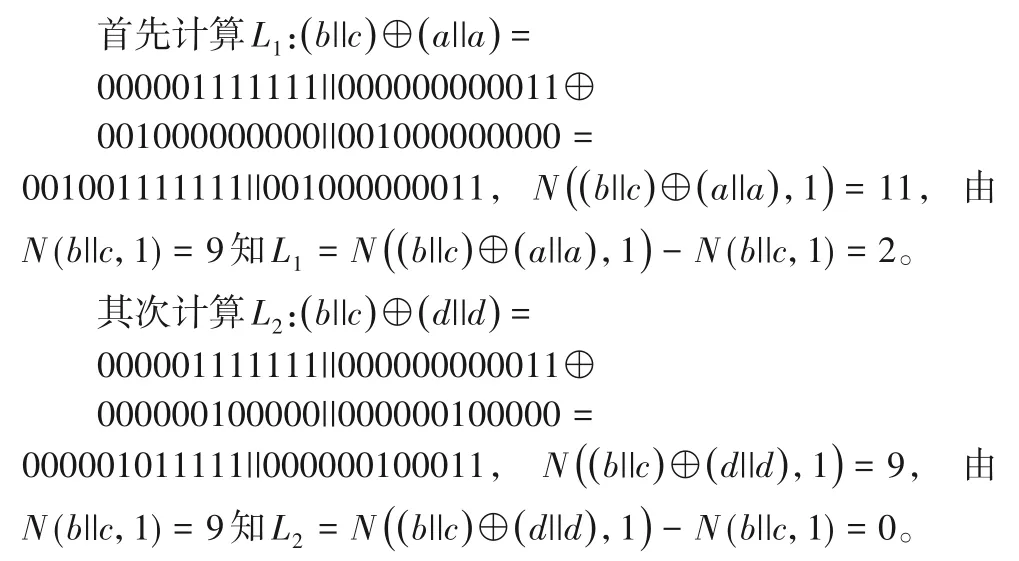
因此(L1，L2)=(2，0)，从而可以断定 [x1，x2]≺=[y1，y2]，即[3，7]≺=[6，10]，得到正确的判断结果。

3 整数区间位置关系判定协议

3.1 协议描述

协议的构造主要基于Goldwasser-Micali 加密体制的异或同态性质：在公私钥对不变的情况下，两个明文比特m1和m2的密文E(m1)和E(m2)模N相乘，结果为m1⊕m2的密文，即E(m1)×E(m2)modN=E(m1⊕m2)，其中N是加 密 运算的模数。协议中还需要用到集合{1，2，…，2n}上的置换，其含义是该集合到自身的一一映射。在协议开始之前，Bob 生成自己的公私钥对，并将公钥告知Alice。协议中的加密都是指用Bob的公钥进行加密，解密都是指用Bob的私钥进行解密。另外，Alice 和Bob 根据实际情况事先约定一个全集U={u1，u2，…，un}，确保他们的秘密区间都是U的子集。

协议1 整数区间位置关系判定协议。

输入：全集U={u1，u2，…，un}是由n个连续整数构成的公开集合，整数区间[x1，x2]⊆U是Alice 的秘密输入，整数区间[y1，y2]⊆U是Bob的秘密输入。

输出：Alice 和Bob 都得知[x1，x2]和[y1，y2]的位置关系（即属于定义2中的哪一种情况）。

Alice和Bob执行如下协议步骤：

1）Bob 按上述0-1 编码规则将区间[y1，y2]编码为n长的两个0-1 编码b=(b1，b2，…，bn)和c=(c1，c2，…，cn)，逐比特加密b||c后得到2n个密文E(b||c)，重复拼接一次后得到b||c||b||c的4n个密文：

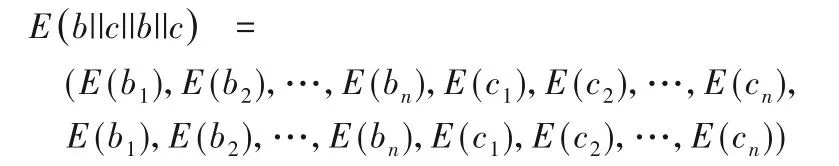
将这4n个密文发送给Alice。

2）Alice 按上述0-1 编码规则将[x1，x2]编码成长度为n的两个0-1 编码a=a1a2…an和d=d1d2…dn，逐比特加密a后得到n个密文E(a)，逐比特加密d后得到n个密文E(d)。然后拼接成a||a||d||d的4n个密文：

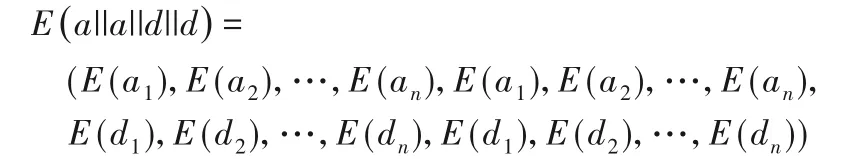
Alice 将这4n个密文E(a||a||d||d)与Bob 传来的4n个密文E(b||c||b||c)进行逐项对应模N相乘（异或同态运算），得到4n个密文：

Alice 秘密地独立选取{1，2，…，2n}上的两个随机置换T1和T2，对这4n个密文的前2n个密文用T1进行随机置换，后2n个密文用T2进行随机置换，将置换后的4n个密文发送给Bob：

3.2 正确性和安全性分析

本节在半诚实攻击者模型下给出协议1 的正确性和安全性证明，其中半诚实攻击者模型假定协议的每个参与方都严格地遵循协议步骤，但允许它们记录自己在执行协议过程中的中间信息，以此去推测对方的秘密输入。在此模型假设下，定理2证明了执行完协议后参与方将输出正确的结果，定理3证明执行完协议后参与方的隐私输入数据未被泄露。

定理2正确性。在半诚实攻击者模型下，协议1正确地判断整数区间的位置关系。

证明 在半诚实模型下，Alice 和Bob 都严格遵循协议步骤。容易得到下面的关系：

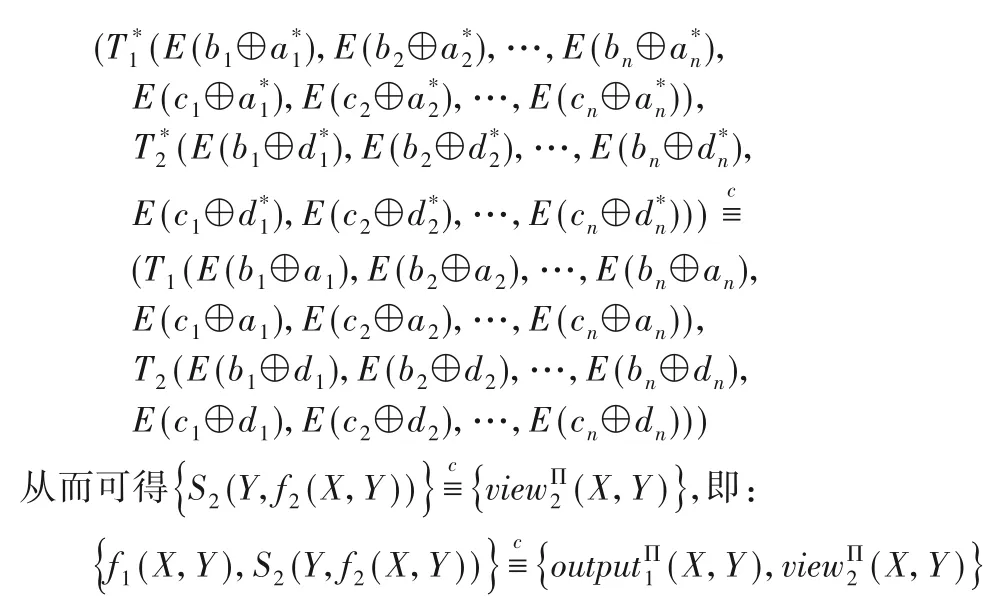
4 效率分析与比较

本文首次提出并研究整数区间位置关系问题，故没有前人的解决方案进行直接比较。考虑到文献［19］的协议1（简记Chen 协议）解决的是保密判断一个整数点a是否属于一个整数区间［x，y］的问题，该问题与本文的研究问题相对接近，本章将Chen协议与本文协议的性能进行比较。

整体上看（参见表1），二者的研究思路和技术手段相近，例如都基于Goldwasser-Micali（简记为GM）加密体制，都用到了随机置换思想，都只考虑半诚实攻击者模型。但二者的研究问题并不相同，Chen 协议的输出结果是a∈[x，y]或a∉[x，y]，不能直接扩展来解决整数区间位置关系判定问题。

表1 整体性能对比Tab.1 Overall performance comparison

复杂度比较方面（参见表2），两个协议的轮复杂度、Alice的加密次数和Bob 的加密次数都分别相同，但本文协议的通信复杂度和其他方面的计算复杂度大约是Chen 协议的两倍。导致复杂度增加的主要原因是二者解决的问题不同，Chen 协议仅需对长度为2n的0-1 串进行操作，而本文协议需要对长度为4n的0-1串进行操作。

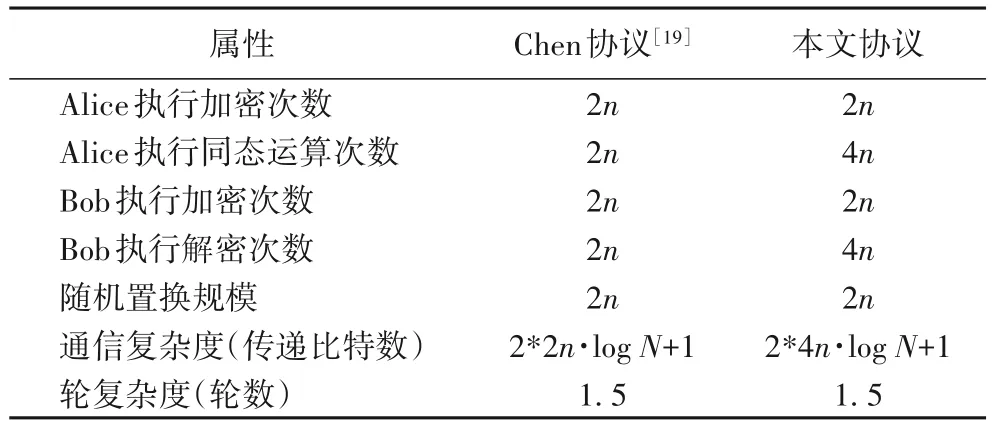
表2 复杂度对比Tab.2 Complexity comparison

对本文协议而言，从其复杂度情况可以看出，n越大意味着计算复杂度和通信复杂度都越高，其中n是全集U的势（U所含元素个数），因此在满足隐私保护要求的前提下，可以选择势n尽可能小的全集U。

5 结语

安全多方计算是当前密码学界的研究热点。本文提出并研究隐私保护整数区间位置关系判定问题，这是一类新的安全两方计算问题，实际生活中的一些隐私保护问题可抽象为该问题。论文首先定义了整数区间的6 种位置关系，并构造了参与方的整数区间的一个0-1编码方案，进而给出了6种区间位置关系的充分必要条件；其次以此充分必要条件为判定准则，基于Goldwasser-Micali 加密体制在半诚实攻击者模型下设计了一个整数区间位置关系判定协议；最后证明了协议的正确性和安全性，并对协议的性能进行了说明。本文首次研究隐私保护整数区间位置关系判定问题，构建的解决方案的复杂度偏高，设计效率更优的解决方案有待进一步研究。