（91913部队 大连 116041）

1 引言

高精度测量系统在低仰角工作条件下，由于受测量装备性能状况、目标特性、多径干扰和后向反射等因素的影响，实际测量值与真值之间存在较大误差，根据误差的性质和特征可分为随机误差、系统误差和过失误差三类。其中的随机误差可以通过改善接收机性能、天馈结构、伺服跟踪性能来减小。过失误差为人为因素，可以通过提高操作人员的水平来避免。对系统误差的修正大多在事后数据处理环节进行。由于精密测量雷达的系统误差一般比随机误差大，此种方法最大的缺点是实时交汇融合的测量数据精度差，特别是在使用测角交汇体制的测控网中误差更大［1］。同轴跟踪技术是解决此类问题的有效手段，可在不改变伺服系统环路带宽的条件下，大幅提高系统测角精度。另外，也可采用将二阶无静差系统升级为三阶无静差系统的方法来提高测角精度，例如采用开闭环复合控制系统和再生反馈控制系统，但这两种系统需要在控制环路中增加许多微分环节，会使系统的噪声迅速增大，工程实现较困难。为减小测角系统误差，文章采用一元线性回归的方法［2］，对单台测量雷达的测角系统误差进行了实时修正，提高了测控系统的实时交汇精度。

2 系统误差的修正

2.1 系统误差分析

天馈分机的系统误差主要由动态滞后误差、大盘不水平误差、两轴不正交误差、电轴偏斜误差、重力下垂误差构成，其中动态滞后误差主要通过二阶无静差系统的控制系统修正，这里的系统误差修正主要考虑余下四种误差即可。系统误差对测量数据实时精度的影响远大于随机误差，实时对系统误差进行修正可使实时测量精度提高一个数量级，甚至更多。系统误差修正是实现同轴跟踪的关键，文章采用一元线性回归方法对系统误差进行修正。其原理框图如图1所示［3］。

图1 系统原理框图

若分别用字母A、E、k、θ、α、σ、β表示天线的方位角、俯仰角、大盘倾斜角、大盘倾斜最高点方位角、方位俯仰不正交角、电轴偏斜角、重力下垂角，则相应的系统误差如式（1）～（4）所示［4］：

大盘不水平误差：

两轴不正交角度误差：

电轴偏斜误差：

重力下垂误差：

式中的k、θ、α、σ、β是可事先进行精密标校的参数，可以当成常数处理，A、E为编码器输出的天馈系统当前角。

由以上误差的表达式可以看出，两轴不正交角度误差和电轴偏斜误差只在方位角度存在系统误差，重力下垂误差只在俯仰角度存在系统误差。

2.2 测量数据拟合

数据拟合是一种常用的数据处理方法，可以局部消除测量误差的影响。在雷达测量目标特征参数的实际过程中，通过测量数据能否正确揭示某些变量之间的关系，进而正确认识事物的内在规律与本质属性，往往取决于两方面因素［5］。其一是测量数据的准确性或准确程度，这是因为在获取测量数据的过程中一般存在测量误差，导致所讨论的变量成为随机变量。其二是对测量数据处理方法的选择，采用哪种数据处理方法决定了数据的实时或事后处理精度和效果，是否具备应用价值。但由于测量数据客观上总是存在测量误差，而拟合函数大多数情况下是通过经验公式获得的，因此要正确揭示事物的内在规律，往往需要对大量的测量数据进行分析，尤为重要的是进行统计分析。统计分析的方法有许多，如方差分析、回归分析等，这里所采用的统计分析方法就是回归分析［6］。

在科学计算中经常要建立实验数据的数学回归模型，给定一些已知的测量数据，需要用比较简单和合适的函数来拟合实验数据。这种回归模型的特点是［7］：

1）适度的精度是需要的；

2）测量数据有小的误差；

3）对于某些问题，可能有某些特殊的信息能够用来选择实验数据的数学模型。

假设雷达在某次测量中n个时刻t1，t2，t3，…tn测量了n组方位和俯仰值，其值分别为A1，A2，A3，…An和E1，E2，E3，…En，基于误差分析和数据拟合的特点，建立数学回归模型的步骤如下：

1）修正系统误差

为提高雷达装备的测量精度，特别是大型测控网络的测角定位交汇精度，需要在测量过程中实时修正测角系统误差，即对大盘不水平误差、两轴不正交误差、电轴偏斜误差、重力下垂误差进行实时修正［8］。根据式（1）～（4）对测量数据系统误差的分析，那么在ti时刻的方位和俯仰值的系统误差如式（5）和式（6）所示：

其中，∆Ati、∆Eti(i=1，2，3，…n)分别表示ti时刻的方位和俯仰角度的系统误差。

假设误差的修正方法符合一定的函数变换关系，由式（1）～（4）系统误差的表达式可以看出，方位角的系统误差不仅与方位角度有关，而且与俯仰角度有关，俯仰角的系统误差同样如此。因此，修正后的方位和俯仰角度数据可以用如下方法表示：

其中，f、g分别表示修正方位系统误差和俯仰系统误差的变换函数，Ai、Ei分别表示ti时刻的方位和俯仰值，分别表示修正系统误差后ti时刻的方位和俯仰值。

由式（7）和式（8）可以看出，修正后的方位和俯仰角度与方位角、俯仰角、大盘倾斜角、大盘倾斜最高点方位角、方位俯仰不正交角、电轴偏斜角以及重力下垂角等因素有关。

2）线性变换

在雷达测量方位和俯仰的角度数据时，大多数情况下，方位和俯仰的角度不是随时间的变化呈线性的相关关系，而是存在某种曲线关系，那么如何确定回归方程呢？常用的有三种方法：一元线性回归，多项式回归和分段回归。在这里采用一元线性回归的方法，即在某些非线性回归方程中，为了确定其中的未知参数，通过观察数据的变化特征和趋势，往往可以通过变量代换，把非线性回归化为线性回归，然后用线性回归的方法确定这些参数。在常用的方法中，可以作适当的变量代换，假设变量代换的公式如式（9）～式（12）所示［9］：

其中，ϕiA、ϕiE分别表示修正系统误差后方位和俯仰角度分别为时对时间的变换函数，tiA、tiE分别表示ti时刻经变量代换后方位角度和俯仰角度对应的时刻值，ωiA、ωiE表示对方位和俯仰角度的变换函数，uiA、uiE分别表示ti时刻变换后的方位和俯仰值。

3）参数估计

运用式（9）～（12）进行变量代换之后，那么tiA与uiA、tiE与uiE符合线性变化关系。因此，可以根据变量代换后的数据进行一元线性回归分析，首先对方位角度与时间的关系进行拟合，如式（13）所示：

其中，αA、βA均为常数，为因变量，为自变量，表示方位角度随时间的线性变化关系。εA服从正态分布的随机变量，假设有n组测量数据，那么根据最小二乘法可以得出αA、βA的估计值如式（14）和（15）所示［10］：

根据式（13）可以得出方位角度与时间的一元线性回归模型如式（16）所示：

由于式（16）是便于数据处理而建立的一元线性回归模型，也就是说是根据式（9）和式（10）变换而得到的，而在实际测量中，方位角度与时间不是简单的线性关系，故需要将式（16）进行反变换，即：运用式（9）和式（10）将进行反变换，从而得到修正后的方位角度uA与时间tA的真实变化关系。如式（17）所示［11］：

其中，函数γ表示时间方位角度uA与估计参数以及时间tA之间的关系。式（17）刻画了方位角度与时间的真实变化关系，uA为因变量，tA为自变量，表示方位角度随时间的非线性变化关系，是关于以及时间tA的函数，它不是一元线性回归模型。

用同样方法可以计算出αE、βE的估计值出，从而可以得到修正后的俯仰角度与时间的非线性变化关系。

3 仿真计算

雷达在某次测量中，假设在0s～50s内共测量得到5000组方位和俯仰值，由于系统误差的存在，因此，运用式（7）和式（8）修正系统误差，以修正方位和俯仰角度数据，假设修正系统误差的方法如式（18）和式（19）所示［12］：

运用式（18）和式（19）对实测数据进行系统误差修正，得出修正后的方位角度和俯仰角度分别与时间的变化关系如图2和图3所示。

图2 方位与时间的关系

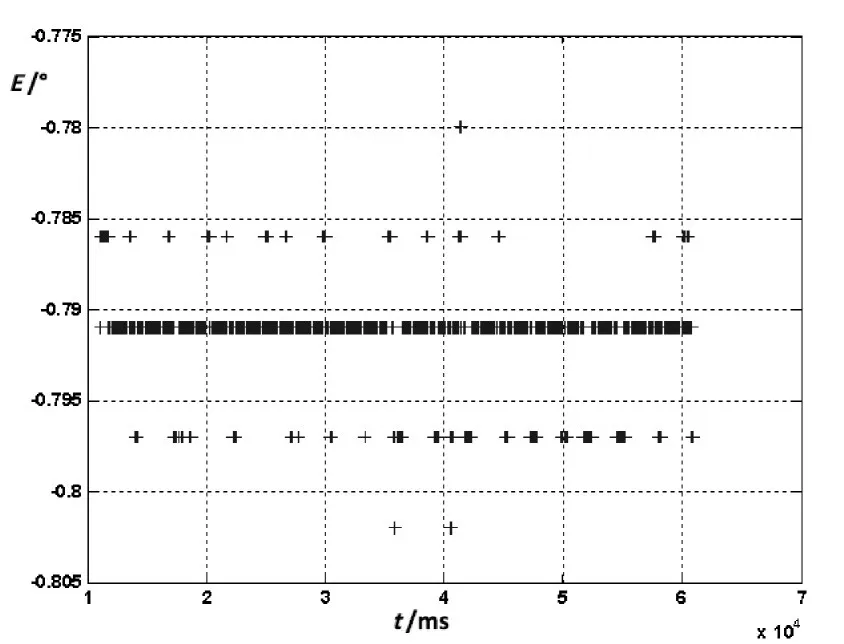
图3 俯仰与时间的关系

由图2和图3可以看出，修正系统误差后，方位、俯仰角度与时间的关系不是一条平滑的曲线，不能有效地对下一时刻的角度进行外推、预测，故将上述角度与时间的关系进行变换，化为一元线性回归，运用公式（14）和式（15）计算得到αA、βA、αE、βE的估计值如下：

将上述估计值代入式（16），得到系统误差修正后方位角度和俯仰角度分别与时间的变化关系，如图4和图5所示。

由图4和图5可以看出，修正后的方位和俯仰角度与时间呈线性变化关系，较好地消除了系统误差，能有效地对角度数据进行外推、预测，提高了测量精度。

4 结语

文章分析了精密测量雷达测角系统误差各因素之间的关系，借见同轴跟踪原理和方法，运用一元线性回归的方法对测角系统误差进行了修正，这种方法较好地结合了定量分析与定性分析的优点，易于确定估计值的统计特性，适用于测量值比较多的情况。在不改变天馈二阶无静差环路极点的情况下，采用外推、预测的方法，可实时修正测角系统误差，对于提高大型测控系统的实时交汇精度有一定的实用价值。

图4 修正后方位与时间的关系

图5 修正后俯仰与时间的关系