何松林，黄 焱，俞 安，任 杰

(1．昆明学院 机电工程学院，云南 昆明 650214；2．昆明学院 物理科学与技术学院，云南 昆明 650214)

分数阶微积分的出现已有300多年的历史，近10多年来得到快速发展并在科学研究及工程技术中受到广泛关注和应用．其中，在粘弹性材料力学性质、反常扩散、信号检测、过程控制等领域采用分数阶微积分的研究已有大量报道[1-4]，且取得很多成果．而由含有分数阶导数项的微分方程描述的动力学系统运动性质的研究变得越来越重要．本文将对类比谐振子建立的分数阶振子模型进行研究，以弄清楚其运动性质．

1 分数阶振子模型

众所周知，谐振子自由振动的微分方程是一个二阶线性常微分方程，而一个只受粘性阻力作用的质点，其运动方程可化为一阶线性常微分方程．

如果质点仅受与其位移随时间变化的分数阶导数成正比的力作用，其运动微分方程可化为分数阶线性常微分方程，这样的系统被称为分数阶振子[5]．

定义运动微分方程为(1)式的质点运动，称为分数阶振子的自由振动．

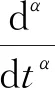
(1)

(1)式中1≤α≤2，分数阶导数采用Caputo定义[6]，并将初始条件记为：

(2)

2 微分方程的解

拉普拉斯变换法是求解常微分方程初值问题的常用方法，其特点在于变换时就考虑到初始条件的影响， 反变换后的结果直接是满足初始条件的特解．对(1)式进行拉普拉斯变换[7]：

(3)

利用Caputo分数阶导数Laplace变换的性质

(4)

得

sαX(s)-sα-1x0-sα-2x1+kX(s)=0，

(5)

整理得：

(6)

Mittag-Leffler函数的Laplace变换公式为：

(7)

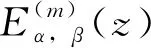
(8)

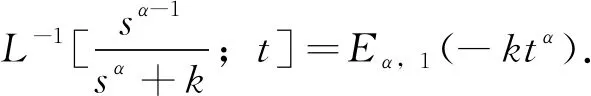
(9)

当β=2,m=0时，(7)式化为：

(10)

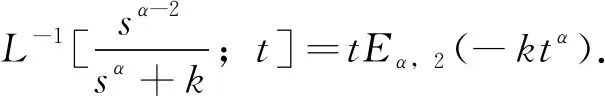
(11)

对(6)式进行Laplace反变换，利用(9)和(11)得方程(1)的解为：

x(t)=x0Eα,1(-ktα)+x1tEα,2(-ktα)．

(12)

3 分数阶振子的运动性质

3.1 阶数为2的分数阶振子表示谐振子

当α=2时，方程(1)化为典型的谐振子运动方程

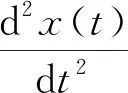
(13)

在此情况下，(12)式化为：

x(t)=x0E2,1(-kt2)+x1tE2,2(-kt2)．

(14)

两参数Mittag-Leffler函数的定义为：

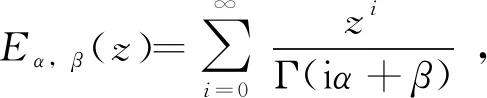
(15)

其中Γ(z)是Gamma函数，当z为整数时，Γ(z)=(z-1)!．由(15)式可推出：

(16)

(17)

利用欧拉公式可得：

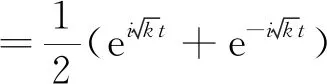
(18)

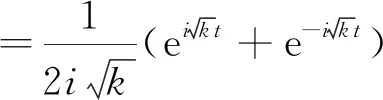
(19)

将(18)和(19)式代入(14)式得：

(20)

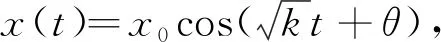
(21)

3.2 阶数为1的分数阶振子表示受粘性阻力作用的质点

当α=1时，方程(1)化为受粘性阻力作用的质点的运动方程

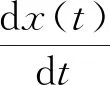
(22)

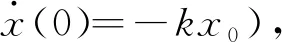
x(t)=x0E1,1(-kt)=x0e-kt，

(23)

与(22)式常规解法得到的结果完全相同．

3.3 分数阶振子的运动状态随阶数和线性项系数变化

设初始速度x1=0，则(12)式简化为

x(t)=x0Eα,1(-ktα)．

(24)

由于Mittag-Leffler函数是大多数人比较陌生的特殊函数，为了能够直观地感受(24)式表示的分数振子位移随时间的变化情况，利用(15)式，编程计算不同值的分数阶振子的位移随时间变化情况．计算中取x0=5 m,k=2 kgmαs-α,α从2变化到1，结果显示如图1．

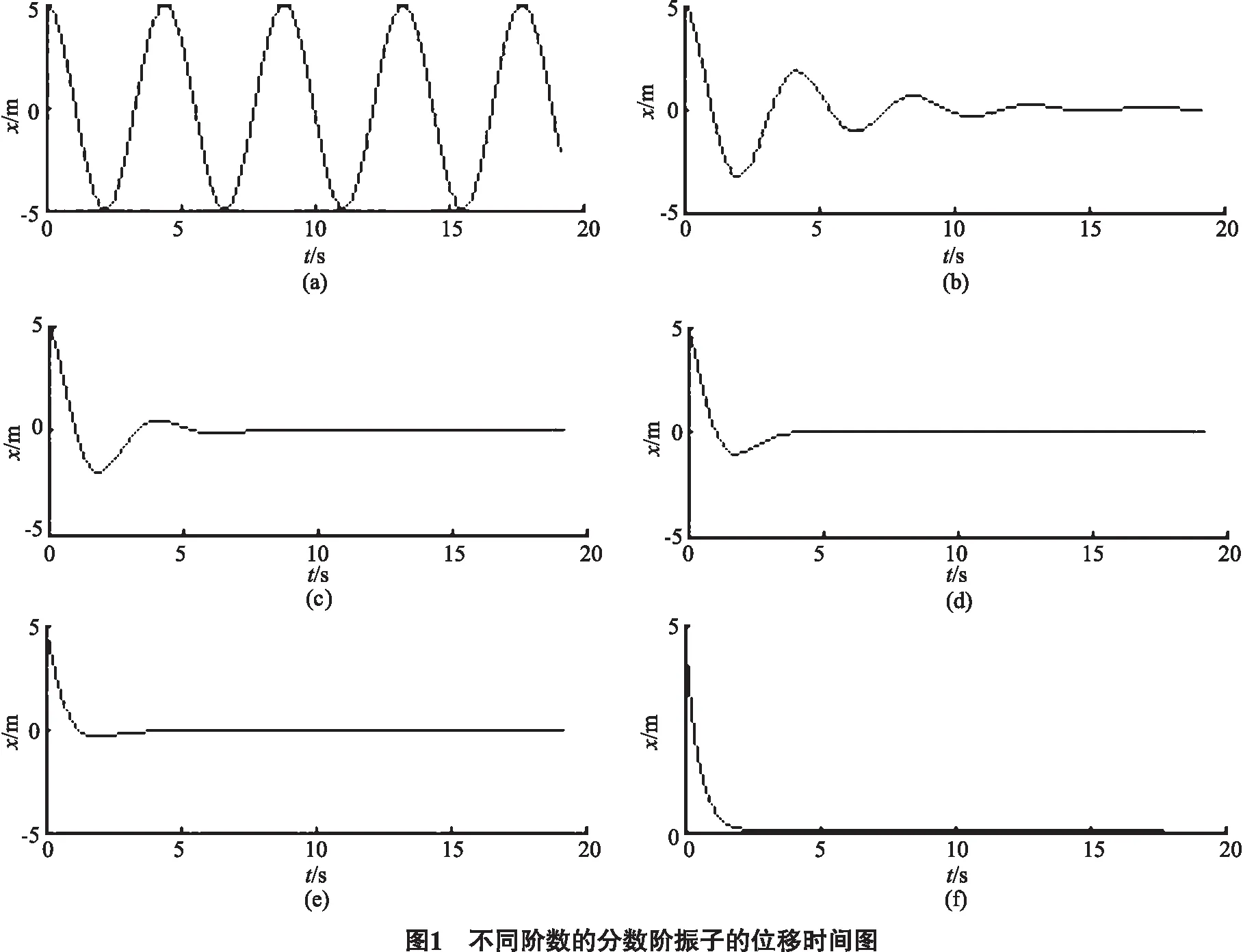
图1中(a)，(b)，(c)，(d)，(e)，(f)中的值分别是2.0，1.8，1.6，1.4，1.2，1.0．从图1可看出，随α值的减小，振幅的衰减加快，同时“欠阻尼”振动时的周期随α的减小而增大．换句话说，α值既影响振子的振幅衰减，同时也影响振动的周期．

为观察线性项系数对分数振子运动影响，取x0=5 m,α=1.8,k分别取0.5，1.0，1.5 kgm1.8s-1.8，按(24)式计算系统位移随时间的变化情况，结果显示如图2．由图2可见，α固定时，随k的增大，振子的振幅衰减加快，振动周期减小．

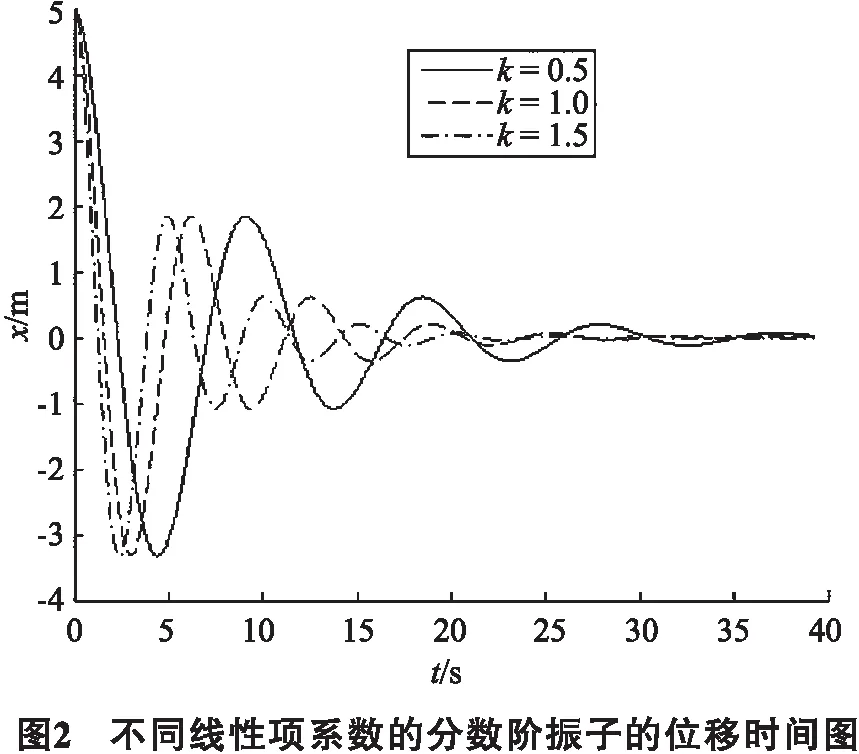
由上面的分析可知，分数振子的自由振动是阻尼振动，这是一种“内禀”的阻尼振动，是系统自身性质决定的．分数阶振子的分数导数阶数和线性项系数都会影响分数阶振子振幅衰减的快慢程度和振动的周期．线性项系数不变时，随分数导数阶数α值的减小，振子振幅衰减逐渐加快，振动周期增大；分数导数的阶数α固定时，随线性项系数的增大，振子振幅衰减加快，振动周期减小．

4 分数振子可采用阻尼谐振子近似代替

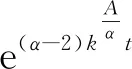
(25)

对参数α,k,x0取不同值的分数振子，用(25)式对由(24)式给出的位移时间数据进行拟合[8]，得到A和B两个常数分别取10/9和1/9时效果最好．即(24)的近似公式为：

(26)

α=1.8,k=1 kgm1.8s-1.8,x0=2 m时的拟合结果见图3，其近似解与精确解符合较好．

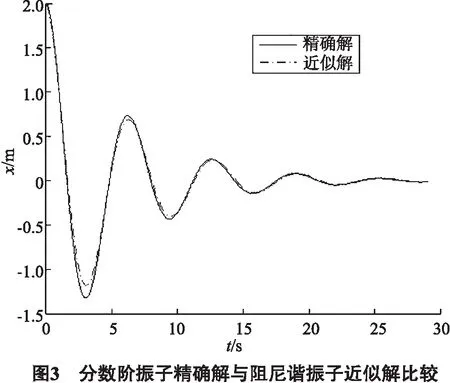
众所周知，谐振子阻尼振动的微分方程为：

(27)

在欠阻尼δ<ω0情况下的解为：

x=Ae-δtcos(ωt+φ)．

(28)

将(28)式与(26)式对比，可得：

(29)

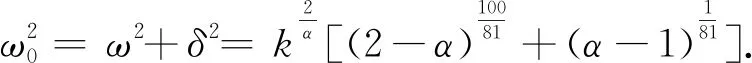
(30)

也就是说在实际应用中，分数振子运动微分方程(1)可以由谐振子阻尼振动微分方程(27)式近似代替，阻尼和刚度分别由(29)和(30)式给出．

综上所述，本文定义了分数阶振子，采用Mittag-Leffler函数求出其自由振动微分方程的解析解，由此得出分数振子的运动性质，证明了谐振子和受粘性阻力作用的质点的运动分别是阶数为2和1的分数阶振子的自由振动；分析得出分数阶振子的“内禀”阻尼振动的振幅衰减及振动周期既与分数导数阶数有关，也与线性项系数有关；提出在工程实践中，可采用谐振子阻尼振动方程近似代替分数振子自由振动方程进行处理．本文的工作，对加深理解含分数导数系统的性质，扩展对“振子”运动的认识，促进含分数导数的系统在实际工程及其他学科研究中的应用有积极作用．