带测度权Dirichlet空间上的复合算子
2020-09-02邱志云曹广福
邱志云, 曹广福
(华南农业大学数学与信息学院, 广州 510642)
引 言
在算子理论的一些基本问题中,解析函数论的相关方法起到了决定性作用,相反地,算子理论也成为探索函数空间的重要工具,这在研究单复变和多复变的本质差异中起到了巨大作用。正是在解析函数论和算子理论的相互发展与碰撞中,复合算子开始进入人们的视线中。由于各函数空间的特征不尽相同,因此,在复合算子的研究中,其有界性和紧性的判定成为众人的首选,相关理论结果有很多而且较为深刻[1]。作为数学研究中的一种常用运算,函数的复合在算子理论中起到了重要作用,在1960年前后开始使用。1987年是复合算子进入热点的时间节点,以Shapiro等人为代表,国内外广大数学工作者对复合算子的有界性、紧性和可逆性等性质的研究热情不断。在1981年以前,大部分关于复合算子的研究是基于单个复合算子的,此后逐渐把函数空间上的所有(有界)复合算子看成一个拓扑空间进行研究,里面的算子也有了范数。
近些年来,复合算子的发展,使得数学中许多重要部分得到了深刻的理解,这也是研究各种空间上复合算子的意义所在[2-4]。复合算子的可逆性、紧性、有界性以及Fredholm性一直受到关注[5-6]。如Bloch空间上的微分复合算子差分的有界性及紧性[7]、广义Fock空间之间的Volterra型复合算子的有界性及其本性范数[8]以及其他空间上的复合算子的可逆性[9-11]等。对连通域上的Bergman空间对可逆和Fredholm复合算子的刻画[12-13]也是复合算子研究的重要成果。随后人们对可乘复合算子的Fredholm性[14]也进行了研究,得出了较为有趣的结果。
Dirichlet空间是与Hardy空间平行的解析函数空间,其函数结构理论很多都依赖于Hardy空间中相应的理论基础[15-16]。在对Dirichlet空间上复合算子的研究中,大多限定在单位圆盘上,也有很多瞩目的成果,本文将其推广到一般域上以及带测度权上,使其复合算子的性质更具有一般性。
令D是C(复平面)上的开单位圆盘,dA表示D上正规化的Lebesgue测度。Dirichlet空间D是由D上具有有限Dirichlet积分的解析函数f构成,使得
在此定义下, D不仅是一个赋范线性空间,而且是一个再生核Hilbert空间,其内积表示为
D的再生核为
令Ω表示C上的连通域,dμ表示Ω上的非负测度。带测度权Dirichlet空间Dμ是由Ω上具有有限Dirichlet积分的解析函数f(z)构成,使得
显然,这里的权与单位圆盘上的权有所不同,更具有一般性。
令M和N表示C(复平面)中两个开、连通、非空子集,简单称它们为域。令L2(M)表示M上有定义的,且相对于M上的测度可平方积分的复值可测函数空间。M的带测度权Dirichlet空间用Dμ(M)表示,它由M所有解析函数构成,满足
用∂M表示M的拓扑边界。点λ∈∂M叫做相对Dμ(M)可去的,如果存在λ的一个的开邻域V,使得对于Dμ(M)上所有函数f,其导数f′皆可解析延拓到M∪V上。用∂μ-rM表示∂M中所有相对于Dμ(M)可去的点组成的集合。用∂μ-eM表示M的Dirichlet本质边界,即∂M中非相对Dμ(M)可去点的集合,因此有
∂μ-eM=∂M-∂μ-rM
本文研究得出了带测度权Dirichlet空间中复合算子的可逆性和Fredholm性质。
1 复合算子的可逆性
定义1令μ是M上一有限正测度。μ被称为M上的Carleson型测度,如果存在常数C>0, 对于任意f∈L2(M,dμ), 有
显然,μ是Carleson型测度当且仅当存在正常数C,使得对于M的任意子集E,有
μ(E)≤CA(E)
其中,A(E)是E的勒贝格测度。
命题1假设M和N表示C中的域,并且ρ是一个从M到N的解析映射,使得dμ∘ρ-1是Carleson型测度。那么Cρ是从Dμ(N)到Dμ(M)的有界算子。
证明由等式
和Carleson型测度的定义,很容易看出Cρ是有界的。
引理1[17]对于C中的任何域G,∂rG的面积测度为零。
定理1假设M和N是C中的域,并且ρ是一个从M到N的非恒定解析映射,使得dμ∘ρ-1和dμ∘ρ都是Carleson型测度。那么Cρ是从Dμ(N)到Dμ(M)的可逆算子当且仅当以下两个条件同时成立:
(1)ρ是单射的。
(2)N-ρ(M)⊂∂μ-r(ρM)。
证明首先证明定理1的必要性。假设Cρ是从Dμ(N)到Dμ(M)的可逆算子,若条件(1)不成立,即若ρ不是单射,则存在z1,z2∈M且z1≠z2,使得ρ(z1)=ρ(z2)。Dμ(M)和Dμ(N)的再生核分别用KM和KN表示。任何符号的复合算子的共轭作用在再生核上,有

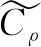
对于∀ω∈ρ(M),很容易有(Cρh)(ρ-1ω)=g(ω),进而h(ω)=g(ω)。因此,Dμ(ρ(M))中的每一个函数延拓到Dμ(N)中的一个函数。这就证明了条件(2)。
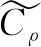
这就完成了定理1的证明。
推论1假设M和N是C中的域,并且ρ是一个从M到N的解析映射,使得∂μ-r(ρM)=φ。若dμ∘ρ-1和dμ∘ρ均为Carleson型测度,则Cρ是从Dμ(N)到Dμ(M)的可逆算子,当且仅当ρ可逆。
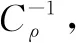
Cρf1=f1∘ρ=g1∈Dμ(M)

因此ρ是可逆的。
接着证明其充分性。由于ρ可逆,逆为ρ-1,那么对任意λ∈N-ρ(M),有ρ-1λ∈M。因为ρ(ρ-1λ)∈ρ(M),则λ∈ρ(M),所以N-ρ(M)⊂∂μ-r(ρM),于是N-ρ(M)=φ,所以M和N的点就一一对应了,因此M和N上的函数也就一一对应了,则Cρ是从Dμ(N)到Dμ(M)的可逆算子。
这就证明了推论1。

从前面的论述可知,如果ρ是单位圆盘D在复平面C上的解析自映射,则Cρ始终是Dirichlet空间或Hardy空间上的有界线性算子,并且Cρ是可逆的,当且仅当ρ可逆。通过定理1,可以看出复合算子的可逆性不等于其符号在复平面中的可逆性。但是,如果域的拓扑边界不包括任何可去点,则复合算子的可逆性就等同于其符号的可逆性。
2 复合算子的Fredholm性
众所周知,在经典解析函数的空间上, 复合算子的可逆性都等同于其Fredholm性,但在带测度权Dirichlet空间上,要将假定条件做一定的改动,才有复合算子的Fredholm性的充分必要条件。
定理2假设M和N是C中的有界域,并且ρ是一个从M到N的非恒定解析映射,使得dμ∘ρ-1和dμ∘ρ为Carleson型测度。那么Cρ是从Dμ(N)到Dμ(M)的Fredholm算子当且仅当:
(1)ρ是单射的,且。
(2)N-ρ(M)⊂∂μ-r(ρM)。

这与Cρ的 Fredholm性相矛盾,因此ρ是单射的,(1)得证。
因为z≠ω,所以当k≥1时,{fk}是一个线性独立序列,并且该序列属于Dμ(ρ(M)),以及fk∉Dμ(N)。因为Cρ(Dμ(N))是Dμ(M)的闭子空间,并且dμ∘ρ为Carleson型测度,所以Dμ(M)/Cρ(Dμ(N))的维度是有限的。


用[fi]表示Dμ(ρ(M))/Dμ(N)中fi的类别。如果{[fi]}是线性相关的,则存在αi∈C,i=1,…,k,并且αi≠0,使得

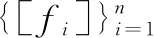

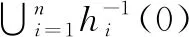

因此有
{z∈∂(ρ(M))||z-p| {p}∪{z∈∂μ-r(ρ(M))||z-p| 因为fi∈Dμ(ρ(M)),所以 因为对于p是fi的极点,有 而{z∈∂(ρ(M))||z-p| 那么就知道fi都在p处解析扩展。也就是每个f1,f2,…,fn都能在p处解析扩展,由于Dμ(ρ(M))是由f1,f2,…,fn和Dμ(N)生成的,因此 那么 因此有 N∩∂μ-e(ρ(M))=φ 通过对各空间上复合算子的研究,将单位圆盘上的Dirichlet空间推广到带测度权的Dirichlet空间Dμ,并对该空间上复合算子的可逆性和Fredholm性进行研究,结合Carleson测度,得出以下两个充要条件: (1)假设M和N是C中的域,并且ρ是一个从M到N的非恒定解析映射,使得dμ∘ρ-1和dμ∘ρ都是Carleson型测度。那么Cρ是从Dμ(N)到Dμ(M)的可逆算子当且仅当以下两个条件同时成立 (a)ρ是单射的。 (b)N-ρ(M)⊂∂μ-r(ρM)。 (2)假设M和N是C中的有界域,并且ρ是一个从M到N的非恒定解析映射,使得dμ∘ρ-1和dμ∘ρ为Carleson型测度。那么Cρ是从Dμ(N)到Dμ(M)的Fredholm算子,当且仅当 (a)ρ是单射的,且 (b)N-ρ(M)⊂∂μ-r(ρM)。

3 结束语
