非均匀多孔介质等效渗透率的普适表达式
2020-07-25刘晓丽王恩志
张 东,刘晓丽,王恩志
(清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
多孔介质渗流问题由来已久,与生活实际和工业生产都密切相关。Henry Darcy在研究均匀砂柱问题时,提出了著名的达西定律,奠定了渗流学科的基础。在此基础之上,学者们针对地下水渗流问题相继提出了地下水运动基本微分方程、Dupuit井稳定渗流公式等,促进了渗流学科的迅速发展[1-2]。直到目前,多孔介质渗流问题仍然是重要而广泛的研究领域,包括孔隙模型和模拟、数值模拟方法改进、多孔介质的非均匀性、非线性渗流、多相流等,整体而言,更趋于微观尺度的非线性渗流性质和渗流过程中的化学-物理机理研究[3-6]。微观尺度考虑多孔介质内部的细观结构,认为介质是非连续性的,存在主要的渗流和储水空间——孔隙和吼道,可以形成明显的渗流通道,计算时建立非连续介质模型,如毛细管束模型、孔隙网络模型等,采用LBM、逾渗理论等方法,根据研究问题可能还会考虑毛细作用、浸润作用等,主要是岩石渗流问题,如油气开采及地热问题等[7-11];而宏观尺度则忽略多孔介质的微观结构,认为大于一定尺度(多孔介质的表征单元体),其微观结构的渗透率趋于稳定,可以用渗透率来反映其渗透性能,认为多孔介质为连续介质,运动方程基于达西定律,多用于工程问题如地下工程、环境工程等。微观尺度的关注并不代表宏观大尺度计算不受重视,反而正如Thomas所总结的:“微观尺度的物理特性决定宏观尺度的模型”[12],正是微观尺度的机理性研究,为宏观模型提供了改进的基础,一系列理论和方法如体积平均方法、混合理论等建立并运用[13]。
纵观微观和宏观尺度研究,多孔介质的渗透性都是重要的研究指标,对于宏观实际工程问题,渗透率是数值计算的基础,渗透率的准确性直接决定模拟结果的精确度;而对于微观尺度研究,渗透率是评价介质特性的重要指标,也是联系宏观问题的纽带[14-16]。渗流问题的多尺度和尺度差异性是一个重大挑战,尤其是工程大尺度模型所带来的巨大计算量,提高计算效率势在必行。
达西定律是线性渗流定律,其适用范围有限,一般认为砂性土地下水渗流,在低雷诺数(Re<10)时服从达西定律[17-19]。但大部分实际工程问题仍然以达西定律作为基本假设进行处理简化[20-22],而目前的商用软件如MODFLOW等许多模块也是基于达西定律而建立的[23-24]。复杂的水文地质条件决定了多孔介质渗透性质在空间的不均匀分布特性,J Koestel测量了某土壤层孔隙结构,发现由于压实和生物作用,1 m内不同深度的土壤的渗透性差异很大[25];水文地质勘探常采用测井法确定地层的渗透性,但试验范围局限于百米,只是整个工程地质模型的局部[26]。因此,研究不均匀介质局部渗透率分布与整体等效渗透率的关系还是很有必要的。
本文基于连续介质的假定,考虑介质的不均匀性,推导多孔介质渗透率空间分布与总体等效渗透率的关系,并进行数值模拟计算的比对。
1 数学模型及验证
1.1 数学模型
本文的渗流模型可以概述为图1的物理模型,本研究仅以水平x方向的渗流特性为代表,左右边界分别为入口、出口,且都为压力边界,即典型的达西压降渗流问题。
压降法是达西渗流试验方法,试验时以水头表示,其本质即水头压力差驱动渗流发生,其模型示意图如图1所示。
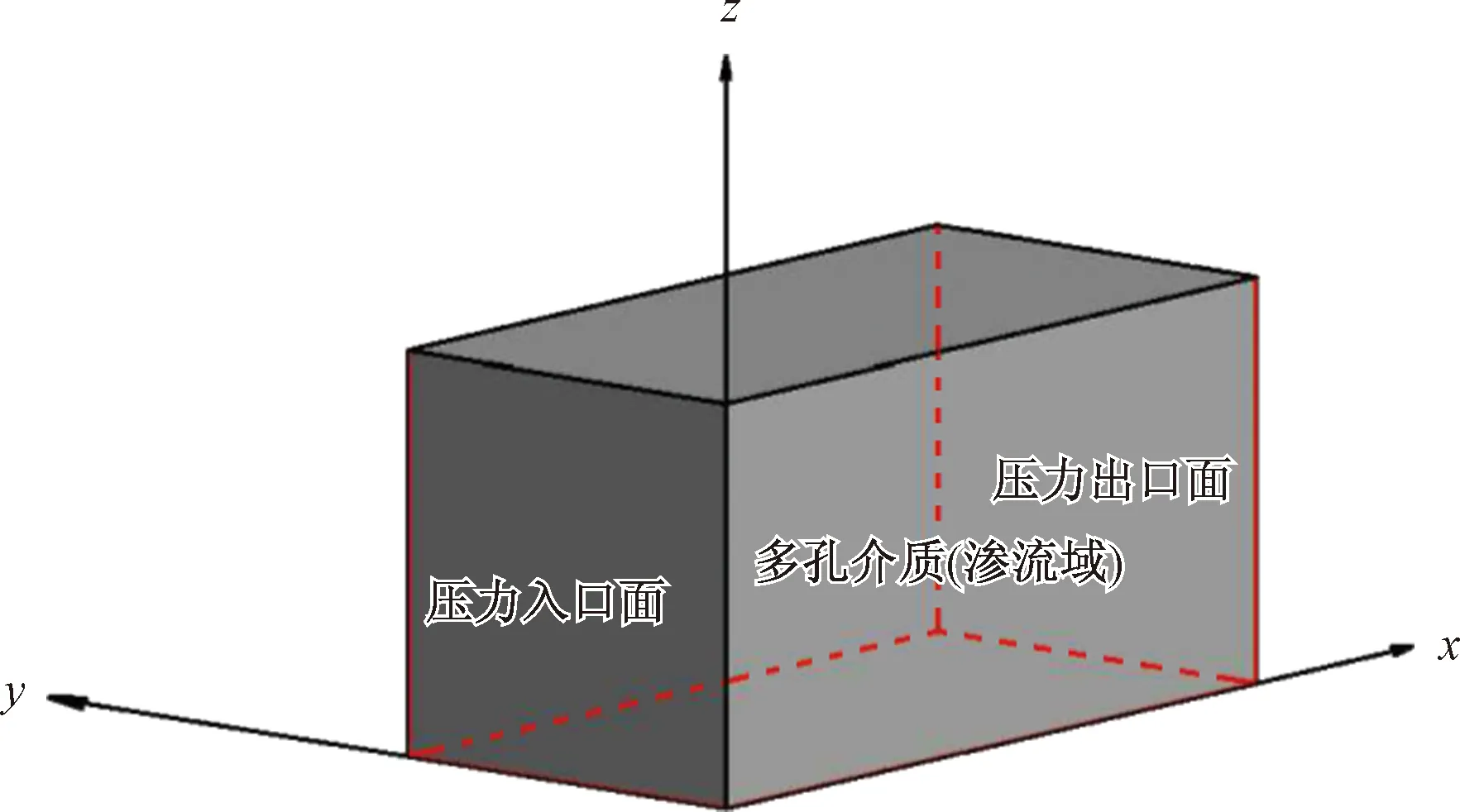
图1 压降渗流试验示意图Fig.1 Diagram of the percolation with pressure drop
数值试验的目的在于得到多孔连续介质的等效渗透率。数值试验定义多孔介质渗透率分布函数κ(x,y,z)是空间位置函数,在不同空间区域渗透率及其变化趋势不同,即建立了非均匀多孔介质模型,基于达西定律探讨了渗透率空间分布与多孔介质总体等效渗透率的关系,并与COMSOL数值模拟的计算值进行了比对分析。
根据压降试验条件建立相应的数学模型(图2)。模型建立所采用的假定为:
(1)多孔介质为连续介质,Lx、Ly、Lz为渗流域的x、y、z方向的长度;
(2)该渗流服从线性达西渗流定律;
(3)假设为饱和渗流,忽略重力作用;
(4)边界位置的速度很小,忽略边界的速度水头,故本研究仅仅考虑压力水头;
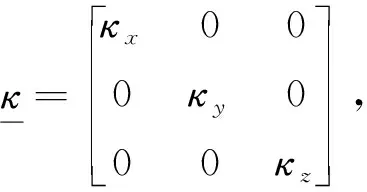

图2 压降渗流数学模型示意图Fig.2 Diagram of the percolation mathematic model
根据上述假设,在多孔介质域内渗流满足达西定律[27-28],即:
v=-K
(1)
式中:K——渗透系数/(m·s-1),由介质和流体性质共同决定;
κ——渗透率/m2,仅与多孔介质的几何结构有关,本文中采用渗透率作为研究指标;
v——断面平均流速/(m·s-1);
μ——流体动力粘滞系数/(Pa·s);
γ——流体重度/(N·m-3)。

(2)

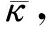
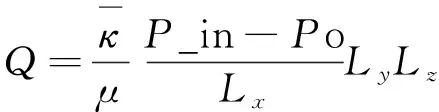
(3)
基于连续介质假定,则在渗流域内任意点(x0,y0,z0)及其邻域可定义渗透率κ(x0,y0,z0),即渗流域内可定义渗透率分布函数κ(x,y,z),渗流域数学模型可表达如下:
渗流域(0≤x≤Lx,0≤y≤Ly,0≤z≤Lz):
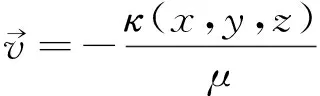
(4)
渗流边界:
1)x=0:p=P_in
(5)
2)x=Lx:p=Po
(6)
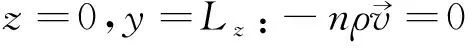
(7)
式中:P_in——入口压力/Pa;
Po——出口压力/Pa;
n——边界的外法向量;
ρ——流体密度/(kg·m-3)。
1.2 数值模拟验证
对式(4)~(7)数值求解即可对渗流流域进行模拟,本文采用有限元COMSOL的达西渗流模块,其控制方程和式(2)一致。按照图2所示,设置相应的边界条件,采用自由四面体网格划分方法和MUMPS算法进行求解。采用不同单元尺寸进行网格剖分,得到一致的计算结果,表明计算结果不随网格尺寸变化。且对单次结果进行流量平衡分析,入口和出口的流量差值小于10-9m3,可认为计算是准确可信的。
2 一维渗透率分布
考虑多孔连续介质域内κ(x,y,z)仅仅与x位置有关,而在y和z方向不发生改变,可退化为一维渗透率分布函数κ(x)。
将式(2)微分化,则在多孔连续介质域内任意一点(x0,y0,z0)及其邻域满足:
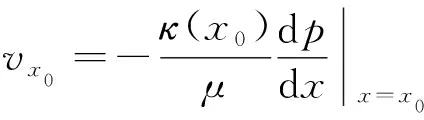
(8)
式中:vx0——渗流域内任意一点(x0,y0,z0)的x方向渗流速率。
结合一维渗流域达西定律并考虑流动的连续性,则有:

(9)
根据式(8)~(9)可以得到多孔连续介质一维渗透率分布与等效渗透率的关系表达式:

(10)

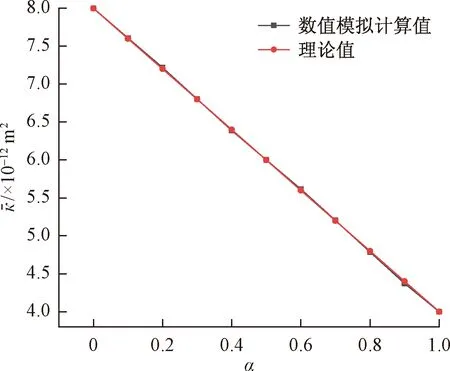
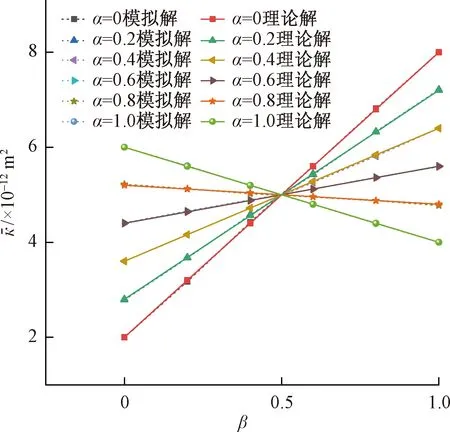
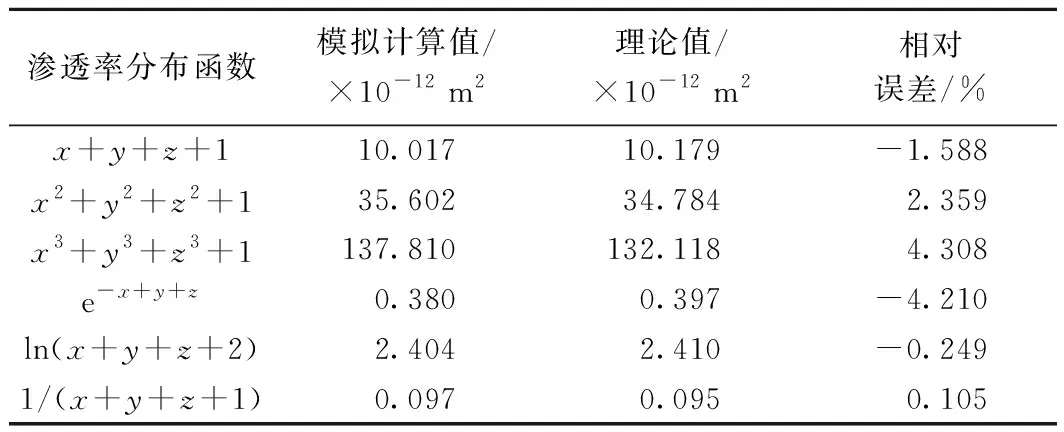
由不同渗透率的介质串联拼接形成的孔隙介质称为复合多孔介质。由2种不同渗透率的介质串联形成的复合介质以数学语言表达,即:0≤x≤αLx区域的介质渗透率为κ1,在αLx (11) 采用COMSOL有限元法进行渗流数值模拟计算,计算几何模型如图2所示,其中Lx=10 m、Ly=5 m、Lz=5 m、P_in=1 000 Pa,Po=0。此外设定不同区域的渗透率参数:κ1=4×10-12m2,κ2=8×10-12m2(下同),以对比验证基于式(10)所得到的推论式(11)。 考虑两种不同渗透率的介质串联形成的复合多孔介质,改变取值并分别利用COMSOL和式(11)计算得到等效渗透率,计算结果如表1所示,相应的曲线如图3所示。 表1 渗透率分段分布函数计算参数及计算结果 图3 数值模拟计算值与理论值对比曲线Fig.3 Numerical and analytical solutions 对于n(n>2)种或以上串联所形成的复合介质亦可根据式(10)求解,当n趋近无穷时,κ(x)即为连续函数。本文中设置κ(x)为不同形式的连续函数,分别利用COMSOL和式(10)计算得到等效渗透率结果如表2所示(其中部分渗透率分布函数难以直接得到数学理论解,则利用MATLAB进行数值积分求解(下同)。一维渗透率分布函数条件下等效渗透率的理论值和模拟计算值的误差小于2%,考虑数值计算的误差,可以认为两者的结果相当吻合,理论推导式(10)是准确的。 表2 渗透率连续分布函数计算参数及计算结果 考虑多孔连续介质域内κ(x,y,z)仅仅与x和y位置有关,而在z方向不发生改变,可退化为二维渗透率分布函数κ(x,y)。则在点(x0,y0,z0)的x方向渗透速率满足: (12) 则在x=x0(∀x0∈[0,Lx])断面平均流量为: (13) 对多孔介质渗透域整体使用达西定律,则有: (14) 根据流动连续性,则得到二维渗透率分布的等效渗透率满足: (15) 显然式(15)是基于x=x0的一系列方程,但压力分布函数p=p(x,y)与κ(x,y)密切相关,难以事先确定,因此式(15)难以直接求得理论解。因此,此处利用上一节的推导结论来简化推导二维渗流率分布函数与等效渗透率的关系。 (16) 对该层使用达西定律,则得到该层的断面平均流量: (17) 则对于整个多孔连续介质区域的断面平均流量,即各分层渗流平均流量的总和,有: (18) 根据流动连续性则可得到二维渗透率分布函数与等效渗透率的关系式: (19) 对于不同渗透率的介质并联拼接形成的介质可以用数学语言表达,即0≤x≤αLx区域的介质渗透率为κ1,在αLx (20) 考虑两种不同渗透特性的多孔介质并联模型,改变α的取值并分别利用COMSOL渗流模拟和式(20)计算得到等效渗透率,计算结果如表3所示,相应曲线见图4。 表3 渗透率二元分段分布函数计算参数及计算结果 图4 数值模拟计算值与理论值对比曲线Fig.4 Numerical and analytical solutions 对于n(n>2)种或以上并联所形成的复合介质亦可根据式(19)求解,当n趋近无穷时即为连续函数。本文中设置为不同形式的二元连续函数,分别利用COMSOL和式(19)计算得到等效渗透率结果(表4)。 二维渗透率分布函数条件下等效渗透率的理论值和模拟计算值的误差小于5%,考虑数值计算的误差,可以认为两者的结果相当吻合,理论推导式(19)是准确的。 表4 渗透率二元连续分布函数计算参数及计算结果 考虑多孔连续介质域内κ(x,y,z)在x,y,z方向都具有差异性,则在点(x0,y0,z0)的x方向渗透速率满足: (21) 则在x=x0(∀x0∈[0,Lx])断面平均流量为: (22) 对多孔介质整体使用达西定律,则有: (23) 根据流动连续性则得到三维渗透率分布的等效渗透率满足: (24) 同上,式(24)难以直接求得理论解。因此,此处利用上一节的推导结论来简化推导三维渗流率分布函数与等效渗透率的关系。 (25) 对该层使用达西定律,则得到该层的断面平均流量为: (26) 则对于整个多孔连续介质区域的断面平均流量即各分层渗流平均流量的总和为: (27) 根据流动连续性则可得到三维渗透率分布函数与等效渗透率的关系式: (28) 构建三维非均匀多孔介质,其渗透率分布函数如式(29)所示。 (29) 根据式(28),可以得到理论解: (1-α)(1-β)κ4 (30) 根据建立的非均匀多孔介质模型,改变α,β的取值并分别利用COMSOL和式(30)计算得到等效渗透率,计算结果如图5所示,理论值和模拟计算值几乎完全重合,误差极小。 图5 数值模拟计算值与理论值对比曲线Fig.5 Numerical and analytical solutions 本文中设置κ(x,y,z)为不同形式的三元连续函数,分别利用COMSOL和式(28)计算得到等效渗透率结果(表5)。 三维渗透率分布函数条件下等效渗透率的理论值和模拟计算值的误差小于5%,考虑数值计算的误差,可以认为两者的结果相当吻合,理论推导公式(28)是准确的。 表5 渗透率三元连续分布函数计算参数及计算结果 (1)针对一维、二维、三维渗流模型,基于连续介质假设和达西定律,通过理论推导得到了等效渗透率的理论表达式; (2)针对不同区域简单常数κ(x,y,z)分布,即不同渗透特性的多孔介质的串并组合模型,发现理论表达式和数值解误差小于5%,充分表明理论推导的准确性; (3)进一步设定了非线性κ(x,y,z)分布,对比分析了理论值和数值模拟解,相对误差也很小,证明了理论表达式的准确性,但随着非线性的增加,误差逐渐增大,这是由于数值计算是通过线性求解所导致的。 本文所构建的非均匀多孔介质等效渗透率理论表达式,为简化复杂地质模型,减少计算量,为快速计算模拟提供了理论支持,还有利于模拟计算结果的合理性快速评估。此外,本文所设定的渗透率分布函数都比较简单,针对实际情况构建复杂的渗透率分布函数以及其对于等效渗透率的影响还有待更进一步的研究。
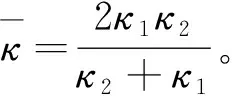
3 二维渗透率分布
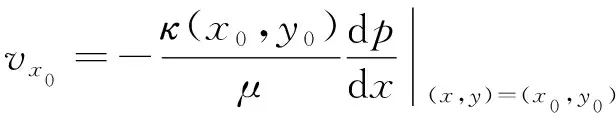

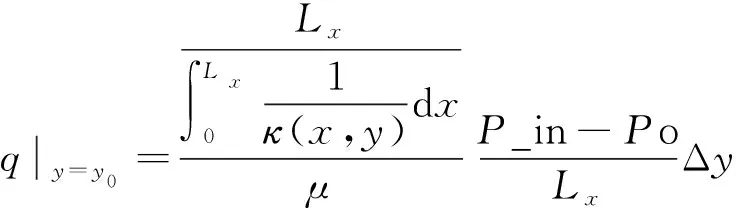

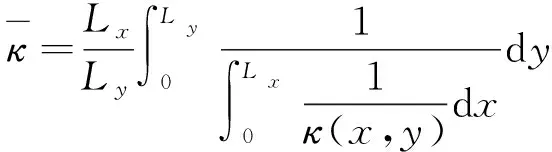


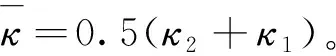


4 三维渗透率分布
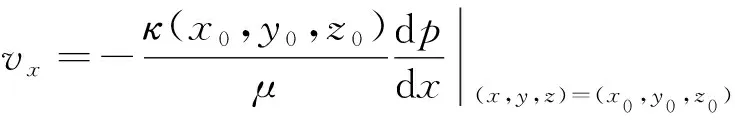

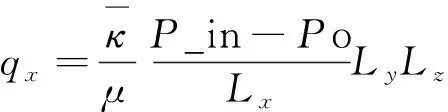


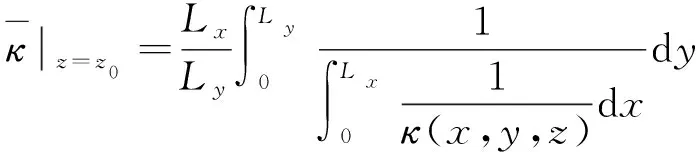
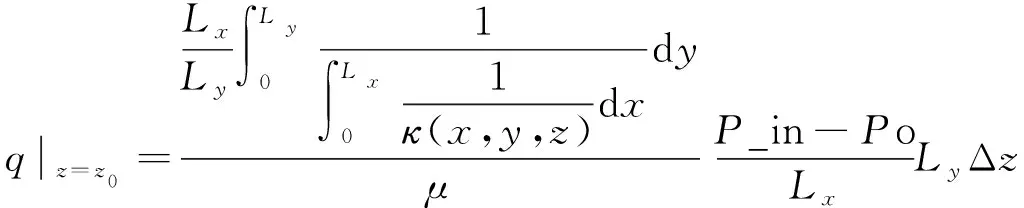
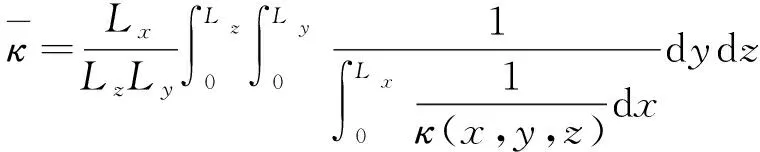

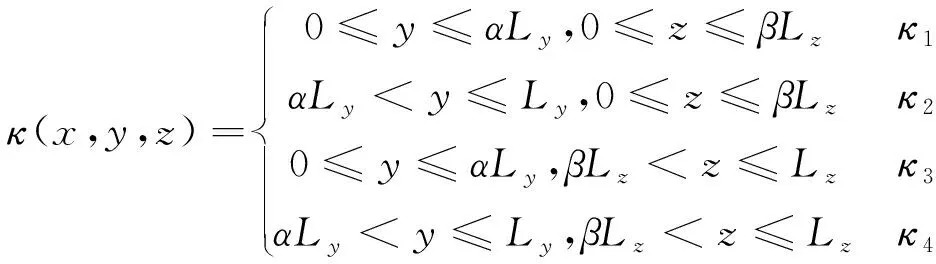

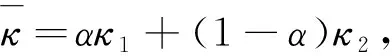
5 结论
