许景生

（岭南师范学院 基础教育学院，广东 湛江 524037）

陈燊年、洪清泉等系统地研究了介质为各向异性（限于有且只有三个正交主轴方向的电介质）的电磁场[1]，其中各向异性电介质拉普拉斯方程的定解问题是各向异性电介质静电场的基本问题之一。拉普拉斯方程的定解问题可分为有限域和无限域两种情形，求解有限域拉普拉斯方程的方法有分离变量法、角基函数法、变分正则法和变分迭代法等，其中分离变量法较常用[2-5]；求解无限域拉普拉斯方程的方法有积分变换法、分离变量法等，其中积分变换法较常用[6]。分离变量法和积分变换法均可求解无限域拉普拉斯方程，但这两种解法求得的解具有不同的数学形式。分离变量法求解无限域拉普拉斯方程，除了方程和边界条件必须是齐次的之外，对区域的形状也有明显限制，要求空间区域的边界面必须是正交曲面坐标系的坐标面；若空间区域是无限域的，本征值将过渡为连续谱，则求得的解及解中的展开系数用傅里叶积分表示。陈燊年等、李文略等应用分离变量法求解有限域拉普拉斯方程的定解问题[1，7-9]，但未涉及各向异性电介质无限域拉普拉斯方程的定解问题。李文略等研究了三维或二维无限域泊松方程的定解问题，其中涉及了应用积分变换的求解方法，但并未涉及验证两种解的等价性[10-11]。顾樵[12]分别应用分离变量法和积分变换法求解热传导稳定温度场的拉普拉斯定解问题，并指出结果是等价的。受此启发，本研究分别应用分离变量法和傅里叶变换法求解各向异性电介质二维无限域拉普拉斯方程的定解问题，并举典型算例间接验证所得解的等价性。

1 各向异性电介质二维无限域拉普拉斯方程定解问题的确定

设各向异性电介质1和电介质2有相同的主轴坐标系O- x1x2x3，坐标面O- x1x3为这两种电介质的分界面，在分界面上方（x2＞0的区域）充满各向异性电介质1(设ε11、ε22、ε33分别为电介质1沿着主轴坐标系x1轴、x2轴、x3轴的介电常数)，在x2≤0的区域充满各向异性电介质2。电介质1所在的区域是无源的，且其中的电势分布仅用O- x1x2平面即可确定，例如在电介质2中过x2轴并沿着x3轴方向放置一无限长的均匀带电密度为λ的直导线，则该带电直导线在电介质1中激发的电势满足二维无限域拉普拉斯方程的定解问题，该定解问题用方程组表示为

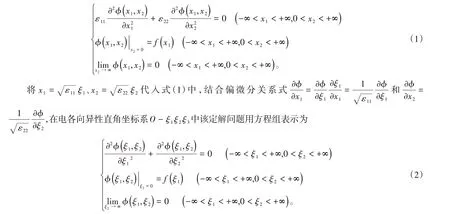
2 应用分离变量法求解二维无限域拉普拉斯方程的定解问题

设式（2）中的泛定方程有分离变量的形式解φ(ξ1,ξ2)= X(ξ1)Y(ξ2)，代入泛定方程中得到

式中，λ为分离常数。

当λ ＜0和λ= 0时，都会导致平庸解φ(ξ1,ξ2)= 0。当λ ＞0时，式（3）中第一个方程的通解为

式中，p、q为任意常数，由于受到式（2）中自然边界条件的约束，故p= 0。

将式（4）和（5）代入形式解φ(ξ1,ξ2)= X(ξ1)Y(ξ2)中，得到泛定方程的解

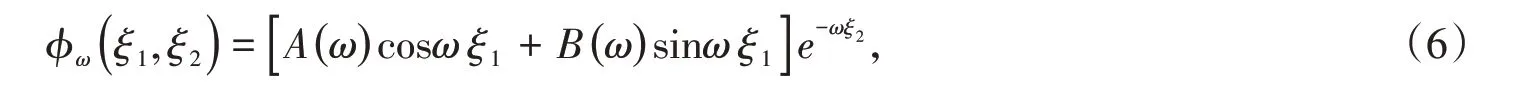
式中，A(ω)= aq，B(ω)= bq。因为泛定方程是线性的，对式（6）进行叠加构成一般解，因为ω是连续变化的，所以一般解是对ω的连续积分，得

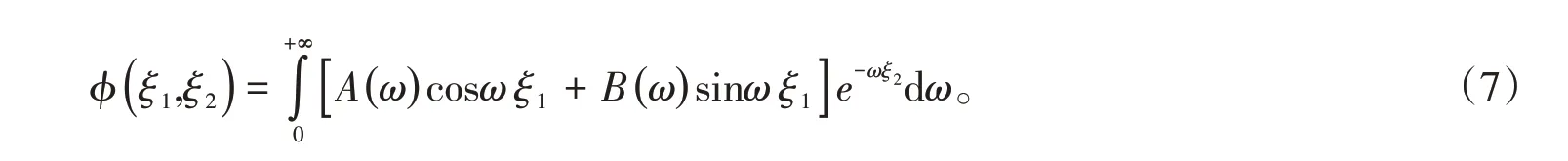
一般解须满足式（2）中的第一类边界条件，有

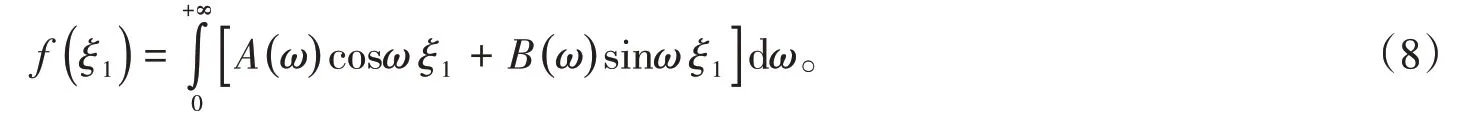
可知，式（8）为边界函数f(ξ1)的傅里叶积分表示式，可得展开系数

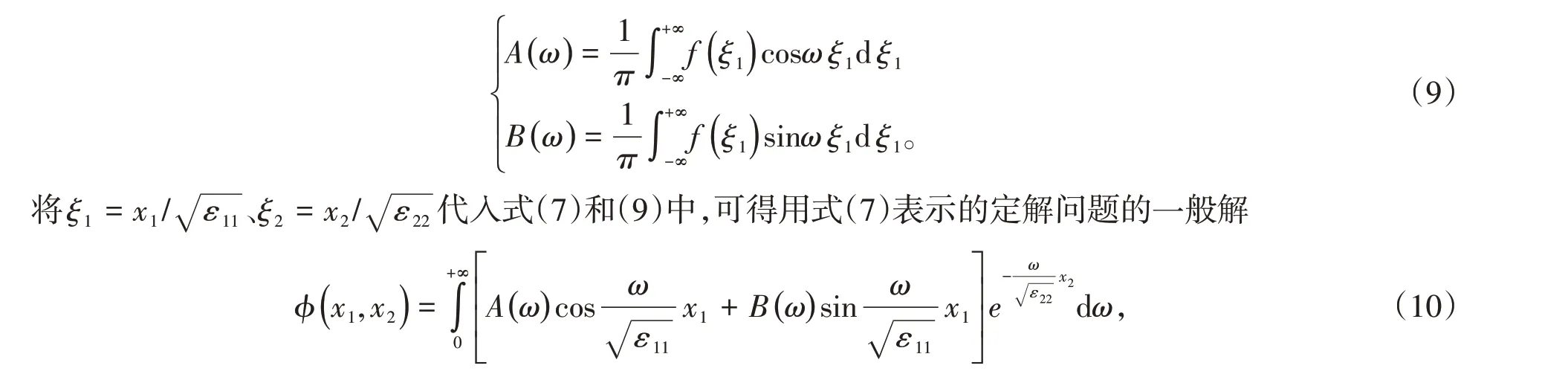
式中，展开系数为

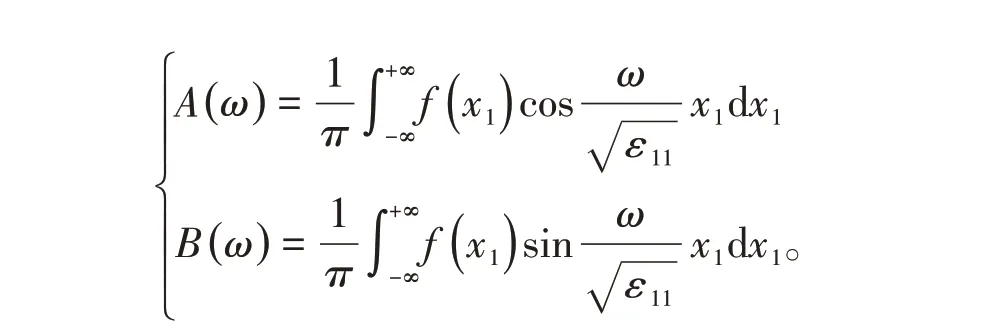
由求解的过程可知，因为分离常数λ是连续的，所以求解的过程不出现分立的本征值和相应的本征函数，解是用连续积分（含傅里叶积分）表示的。

3 应用傅里叶变换法求解二维无限域拉普拉斯方程的定解问题

由定义域-∞＜ξ1＜+∞，可对式（2）取关于ξ1的傅里叶变换

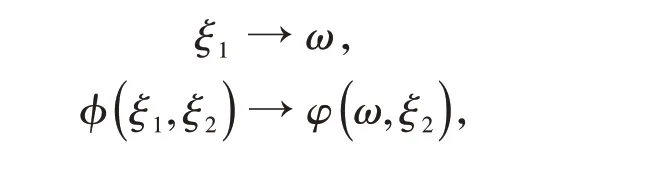
有

式（11）中泛定方程的通解为

式（12）须满足式（11）中的第一类边界条件，故有φ(ω,0)= F(ω)= C，将其代入式（12）中，得

对式（13）作傅里叶反变换

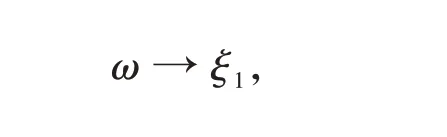
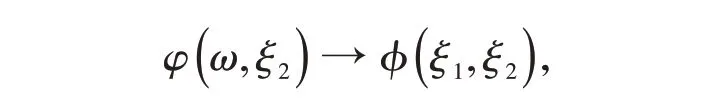
有

式中，“*”号表示傅里叶卷积。应用傅里叶变换法求解该定解问题时，所得的解用傅里叶卷积表示。

4 列举算例间接验证解的等价性

应用分离变量法或傅里叶积分法求解式（1）表示的各向异性电介质二维无限域拉普拉斯方程定解问题，所得的解用式（10）或式（15）表示，显然解的具体数学形式不一样。由静电场的唯一性定理可知，这两种解必然是等价的。现举三个典型的例子间接验证解的等价性。

（Ⅰ）设f(x1)= 0，将f(x1)代入式（10）中，有A(ω)= B(ω)= 0，φ(x1,x2)= 0；对于式（15）而言，f(τ)= 0 即是f(x1)= 0，将其代入式（15）中，亦可得φ(x1,x2)= 0。

对应这种情形的物理模型可以是各向异性电介质1 和电介质2 的分界面处放置接地的无限大导体平面。由所得结果φ(x1,x2)= 0可知，接地导体平面上方电介质1所在的区域是静电屏蔽的，俩解是等价的，符合物理客观事实。

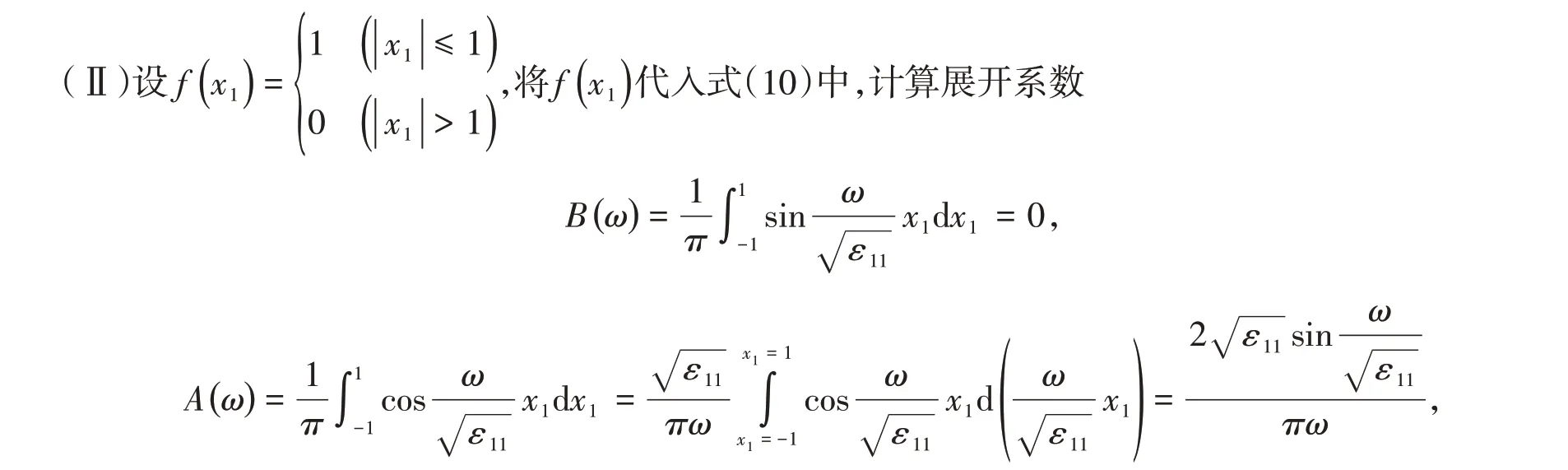
则解为

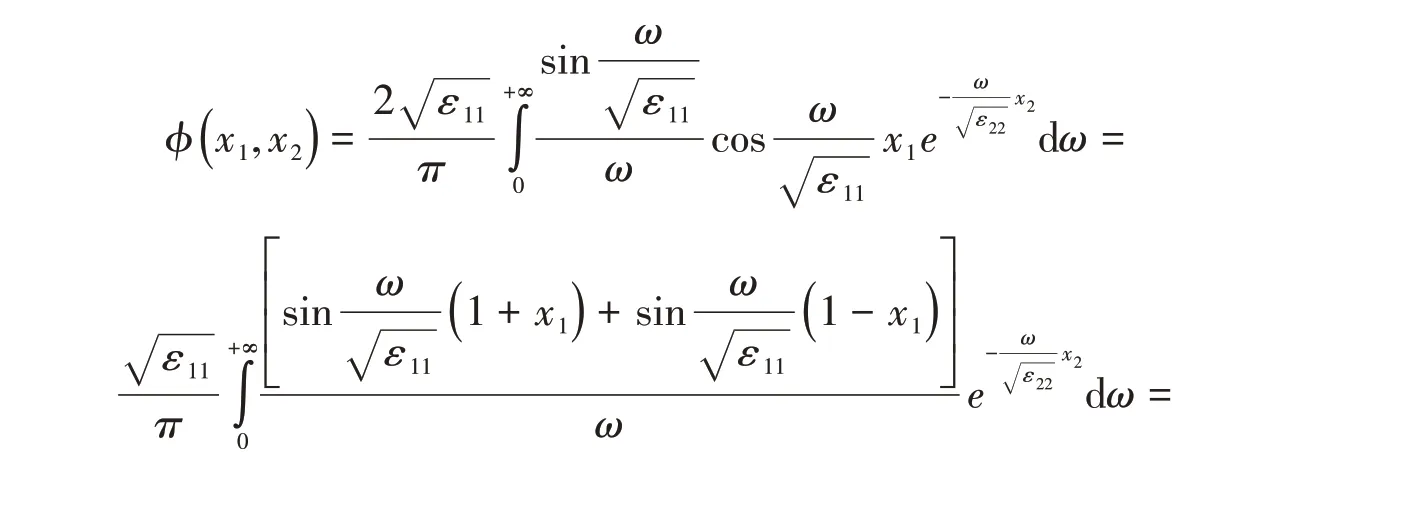
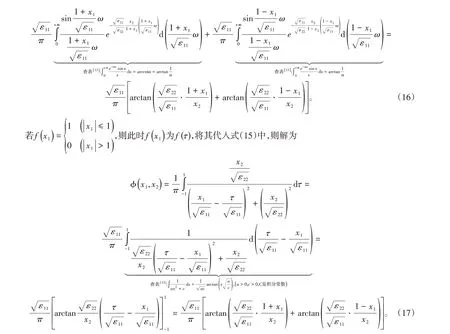
可知式（16）和（17）表示的解是相等的。对应这种情形的物理模型可以是各向异性电介质1和电介质2的分界面处放置了三片无限大的导体平面，分别位于( - ∞＜x1＜-1)和(1 ＜x1＜+∞)区域的导体平面接地，而位于( - 1 ≤x1≤1)区域的导体平面是不接地的等势体。由所得的结果可知，无限大平面上方电介质1所在的区域不能实现静电屏蔽，电势分布由式（16）或（17）描述。

则解为

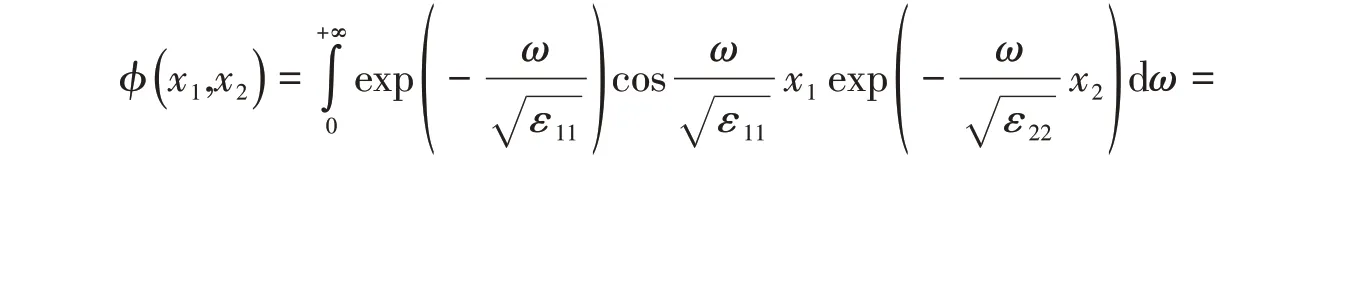
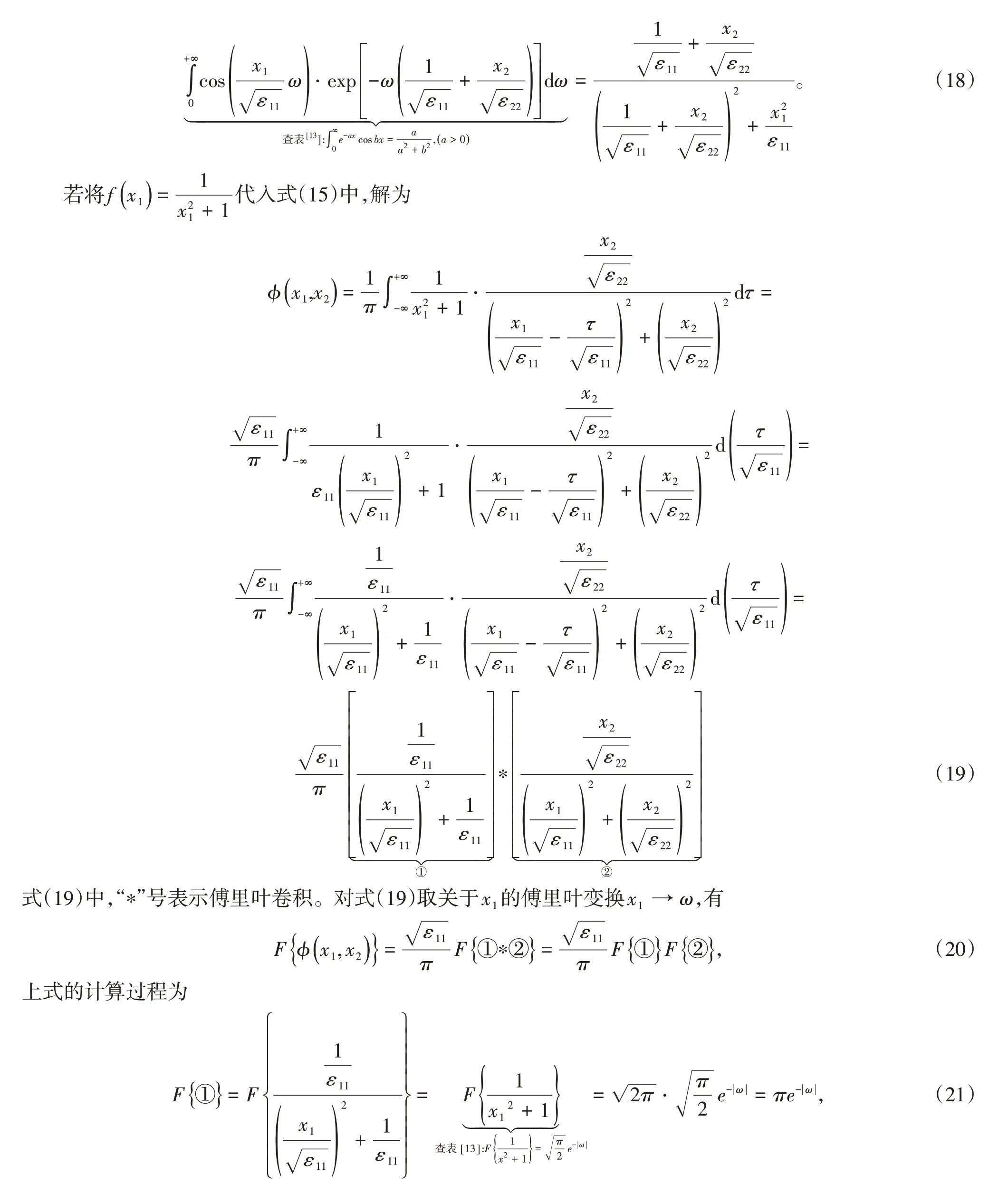
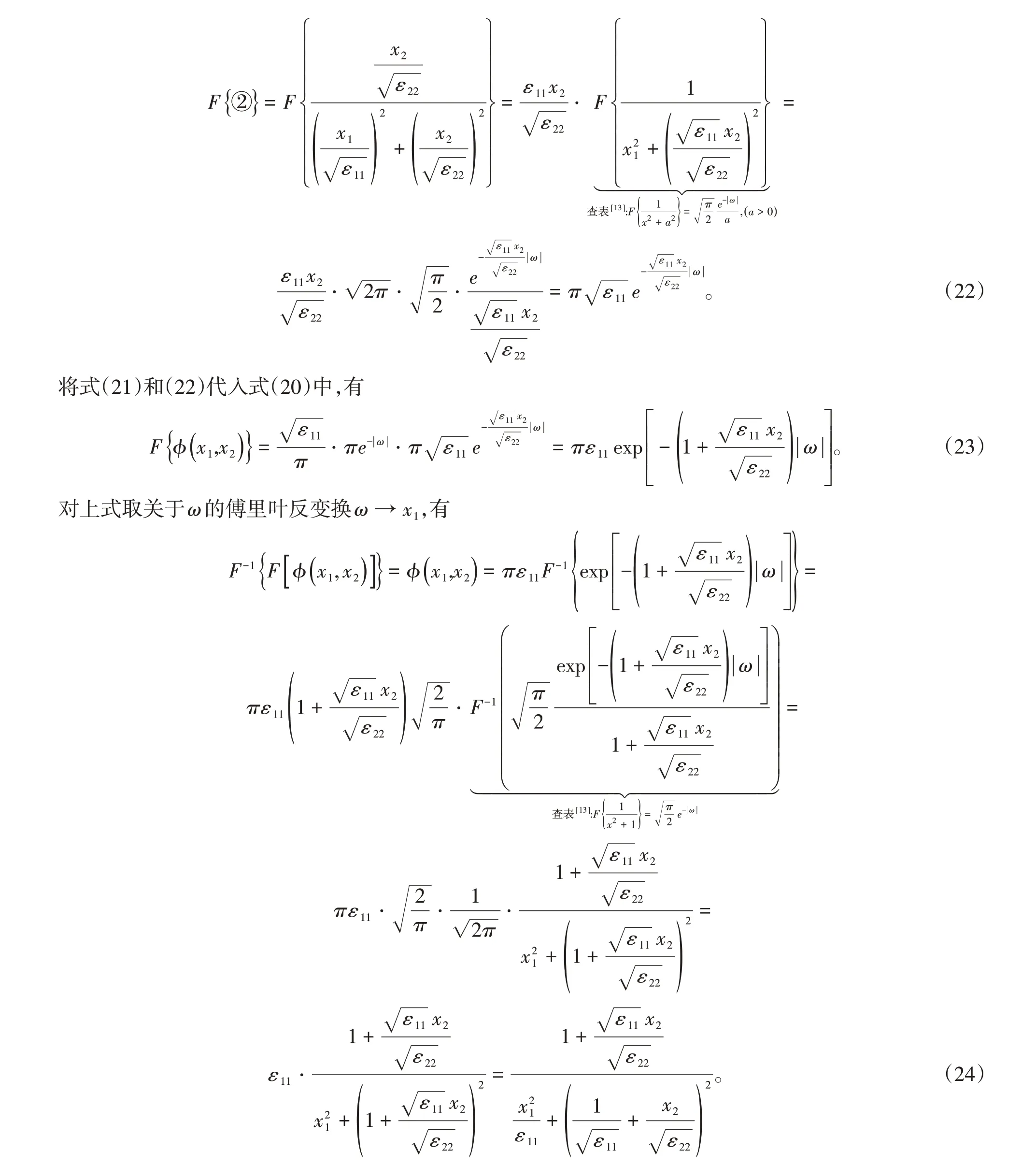
可知式（18）和式（24）表示的解是相等的。对应这种情形的物理模型可以是在各向异性电介质1和电介质2的分界面下方（电介质2所处的区域）有电荷分布，此时电介质的分界面不再是等势面，分界面处的电势关于主轴x2轴对称，且电势随着远离主轴x1轴而衰减。电介质分界面上方区域无源，电势满足拉普拉斯方程，电势分布由式（18）或式（24）描述。

综合以上的计算过程可知，在求解各向异性电介质二维无限域拉普拉斯方程定解问题时，总是先将主轴坐标系中描述的定解问题[由方程组（1）表示]通过变量代换转化为在电各向异性坐标系中来描述[由方程组（2）表示]，求得解之后再通过变量逆变换得到在主轴坐标系下的解，这是研究各向异性电介质泊松方程（或拉普拉斯方程）常用的方法。由静电场的唯一性定理可知，分别应用分离变量法和傅里叶变换法求得的解是等价的。以上所举例子中表示第一类边界条件的函数f(x1)有取零的特殊情形、有取分段函数的情形也有取连续函数的情形，且均给出了与这三种情形相对应的物理模型，由此可推断解的等价性具有普遍性也符合物理客观事实。若要直接证明两种数学形式的等价性，则需证明式（7）与式（14）是相等的，即

观察式（25）可知，要分别求得等号左右两边广义积分的结果，可拓展至复平面上进行计算，但由于函数f(ξ1)或f(η)的具体形式不可知，因而无法确定被积函数的奇点，无法应用留数定理求得结果；若函数f(ξ1)或f(η)的具体形式已知，则相当于给出了特例，即是文中的间接验证其等价性的方法。

若两各向异性电介质分界面上方和下方的区域分别填充的是介电常数分别为ε1和ε2的各向同性电介质，则文中描述的各向异性电介质二维无限域拉普拉斯方程的定解问题可过渡为各向同性电介质二维无限域拉普拉斯方程的定解问题。若将ε11= ε22= ε33= ε1代入式（10）中，可应用分离变量法求得

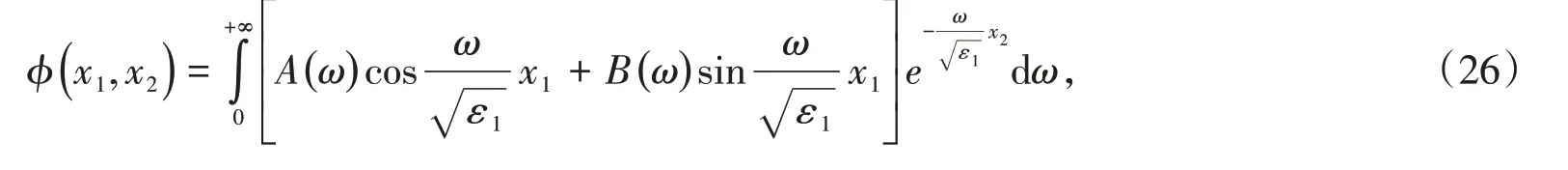
式中，展开系数为

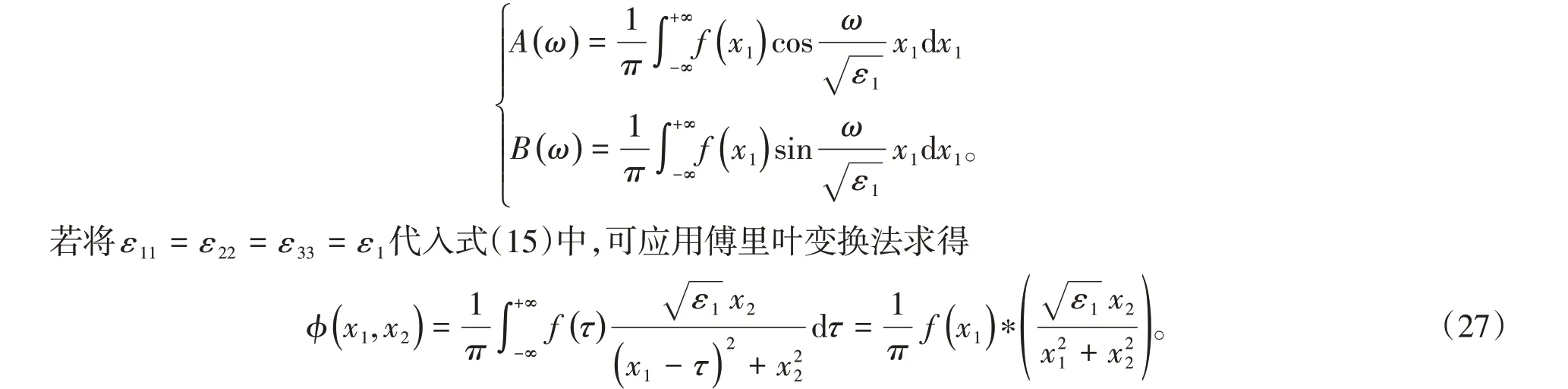
式（26）和式（27）是等价的，可用算例间接验证，计算过程在此不再赘述。