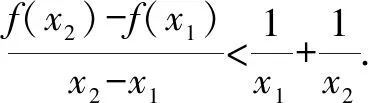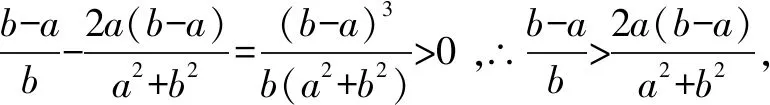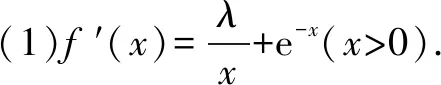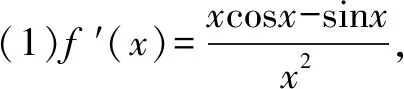武 婷 黄光鑫

(四川省成都市四川师范大学附属中学 610000)

一、引言

拉格朗日Lagrange中值定理本是微分学中的一个重要定理，不在高中数学课本范畴之内，是否有必要教给学生呢？我们先看下面一个问题：

C.f(x)=ex+1D.f(x)=sin(2x+1)

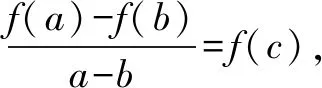
对于A选项：f′(x)=3x2-6x+3∈[0,+)，f(x)∈R，不满足性质T，符合题意.对于B选项：f令x=tanα，则f′(x)转化为当sin2α，cos2α>0时，则由四元均值不等式可知：当且仅当时，等号成立.∵g(α)为奇函数，∴f不满足性质T，符合题意.对于C选项：f′(x)=ex+1，f(x)∈R，f′(x)∈R，满足性质T.对于D选项：f′(x)=2cos(2x+1)，f(x)∈[-1,1]，f′(x)∈[-2,2]，满足性质T.综上：选A,B.

从上面的解法可以看出，对于学有余力的学生而言，对于想参加高校自主招生考试或者想参加数学竞赛的学生而言掌握拉格朗日中值定理也是很有必要的！

二、拉格朗日Lagrange中值定理

拉格朗日Lagrange中值定理:如果函数f(x) 在闭区间[a,b]上连续，在开区间(a,b) 内可导，那么在(a,b)内至少存在一点ξ(a<ξ

三、拉格朗日Lagrange中值定理的应用

下面我们本着由易到难，循序渐进的原则介绍拉格朗日中值定理在解决高中数学题中的应用.

例2 [2019·安徽十校联考]已知函数f(x)=lnx+ax+1(a∈R).(1)讨论函数f(x)的单调性；

解(1)函数f(x) 的定义域为(0,+)当a≥0 时，f′(x)>0，f(x)在(0,+)上单调递增；当a<0时，由f′(x)=0，得若单调递增；若)，f′(x)<0，f(x)单调递减.

综上所述：当a≥0 时，f(x)在(0,+)上单调递增；当a<0时，f(x)在单调递增，在)上单调递减.

(2)证明:由(1)知，当a≥0时，f(x)在(0,+)上单调递增，不满足条件.所以a<0，此时f(x)的极大值为由已知得-ln(-a)=0，故a=-1，此时f(x)=lnx-x+1.不妨设0

例3设函数f(x)=lnx，g(x)=2x-2(x≥1).

(1)试判断F(x)=(x2+1)f(x)-g(x)在定义域上的单调性；

解(1)∵函数f(x)=lnx,g(x)=2x-2(x≥1),F(x)=(x2+1)f(x)-g(x)=(x2+1)lnx-(2x-2) 的定义域为[1,+)当x≥1 时，F′(x)≥0 恒成立，故函数F(x)在定义域[1,+) 上为增函数.

例4 [2019届高三黄冈模拟]已知函数f(x)=λlnx-e-x(λ∈R).

(1)若函数f(x) 是单调函数，求λ的取值范围；

(2)记函数g(x)=e1-x，则函数g′(x)=-e1-x，g(x)在[x1,x2]上满足拉格朗日中值定理的条件，∴∃ξ∈(x1,x2) 使得：g(x2)-g(x1)=-e1-ξ(x2-x1)=e1-ξ(x1-x2).∵x1<ξe1-x1(x1-x2) .