吕小俊，赵凯宏，李 睿

(1.云南大学 旅游文化学院 信息学院, 云南 丽江 674199；2.昆明理工大学 理学院, 云南 昆明 650093)

近几十年来，微分方程模型被广泛地应用于生态系统中，用于描述生态系统内部的变化规律。由于生物系统受到食物供给、气候变化和季节更替等因素的影响，运用周期系统去描述生物竞争系统是非常有必要的，故对生物竞争系统周期现象的研究已成为一个新的热点[1-3]。当种群间没有代级重叠时，差分方程比微分方程更适合于描述种群生态系统。由于离散的差分系统可以提供有效的数值模拟，因此，研究离散生态竞争系统的动力学特征是有意义的。ZHANG等[4]运用叠合度理论研究了带有功能函数的离散食饵-捕食者系统的周期解。同时，LIU等[5]运用Mawhin连续定理研究了以下离散型时滞浮游生态系统的周期解问题：

式中：Ni(k)表示第i个种群第k代的种群密度；ri(k)表示第i个种群第k代的内部增长率；ail(k)表示第i个种群在第k-l代的内部影响率；bil(k)表示第i个种群在第k-l代的种间影响率；cil(k)表示第k-l代第j个种群对第i个种群的抑制率；i，j=1，2，i≠j。

为了促使生态系统的可持续发展，定期种群收获被广泛地应用于渔业、林业和野生动物管理中。因此，有必要在生态竞争系统中增加收获项，从而更加客观、准确地描述生物竞争系统的内部特征。然而，收获项的增加会影响生态竞争系统的多个周期或概周期规则[1,6]。

受以上分析和文献启示，很少有作者研究带有收获项的离散生物种群系统的多解性。因此，在本文中，我们采取Mawhin连续定理去研究以下带有收获项的离散浮游生物系统的多解性问题：

(1)

且Ni(-l)≥0,l=0,1,…,m,Ni(0)>0,i=1,2。式中：hi(k)(i=1,2)表示第i个种群第k代的收获量；ri,ail,bil,cil,hi:Z→R+的ω周期函数，i=1,2,l=1,2,…,m。Z表示整数集，R+表示非负实数集。

1 预备知识

为了描述简单和证明方便，我们需定义以下2个概念：

为了运用引理2证明系统(1)至少存在4个不同的正周期解，需作如下假设：

这里：

引理1的证明过程和文献[4]中引理2的证明类似，故在此不再重复。

(a) 对于任意λ∈(0,1)，x是Lx=λNx的任意解，满足x∉∂Ω∩DomL；

(b) 对于任意x∈∂Ω∩KerL，满足QNx≠0；

(c) deg{JQN,Ω∩KerL,0}≠0。

进一步，作如下定义：

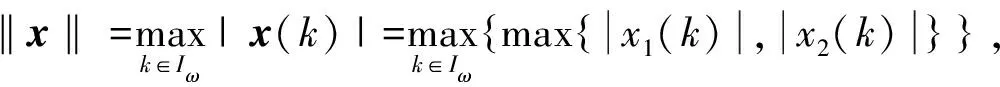
容易验证，lω是一个有限维数的Banach空间。

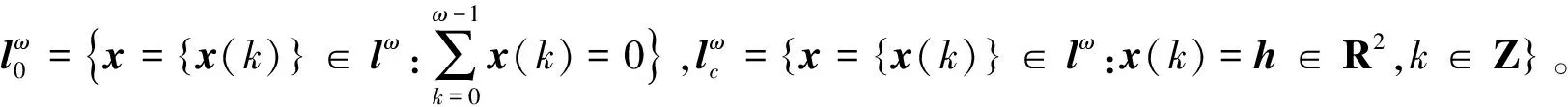
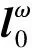
2 4个正周期解的存在性

定理1如果条件(H1)和(H2)成立，则系统(1)至少存在4个ω-正周期解。

证明利用指数变换：N1(k)=exp(x1(k))，N2(k)=exp(x2(k))，将系统(1)重新改写为系统(2)。

(2)

令X=Y=lω,(Lx)(k)=x(k+1)-x(k),x∈X,k∈Z。

(3)

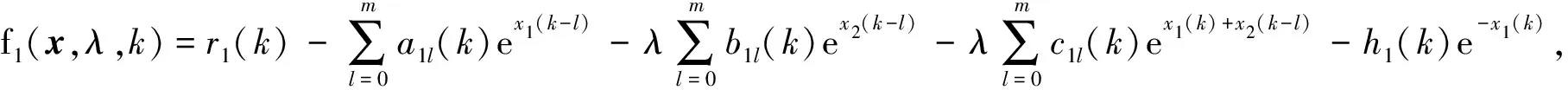
接下来，为了找到满足引理2中所有条件的有界开集Ωi⊂X,i=1,2,3,4。本文考虑方程：Lx=λN(x,λ),λ∈(0,1),即：

(4)

将式(4)中每个等式左右两边关于k从0到ω-1累加，可得：

(5)

和

(6)

由式(4)～(6)，可得：

(7)

和

(8)

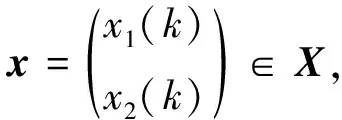
接下来，我们分析式(5)，可得

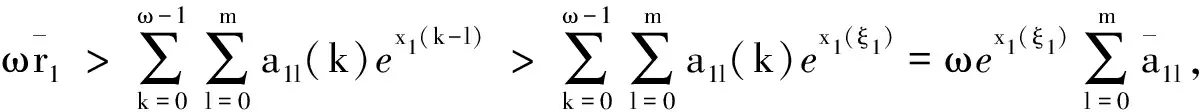
从而，

(9)

进一步，利用不等式技巧分析式(5)，可知

因此，

(10)

同理，由式(6)可得

(11)

再次，利用不等式技巧分析式(6)可知

因此，

(12)

接下来，由式(5)和式(11)可得

进一步，可得

(13)

由式(13)和条件(H1)，可得：

或

结合条件(H1)和以上分析，不难验证

同理，分析式(6)和式(9)可知

由以上分析可得

(14)

结合条件(H2)和式(14)，可得：

或

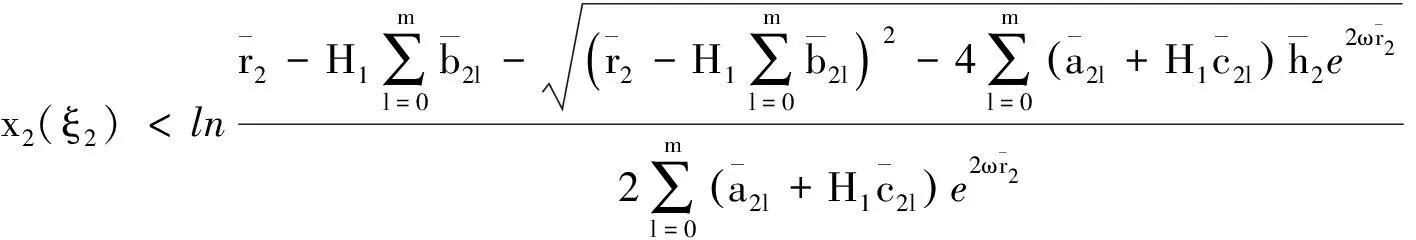
结合条件(H2)和以上分析，不难验证

现构造4个不同的集合Ωi(i=1,2,3,4)：

显然，Ωi(i=1,2,3,4)是空间X上的有界开集，且Ωi∩Ωj=φ(i,j=1,2,3,4,i≠j)。因此，Ωi(i=1,2,3,4)满足引理2的条件(a)。

接下来，我们去验证引理2的条件(b)也是成立的。利用反证法，我们假设当x∈∂Ωi∩KerL=∂Ωi∩R2(i=1,2,3,4)时，QN(x,0)=(0,0)T成立。即，对于常向量x=(x1,x2)T∈∂Ωi，i=1,2,3,4，满足以下的代数方程：

(15)

由于KerL=ImQ，令J=I。由Leray-Schauder度的定义直接计算，可得

因此，引理2的条件(c)成立。

综上所述，Ωi(i=1,2,3,4)满足引理2的所有条件，由引理2可知，系统(2)至少存在4个不同的ω-正周期解。所以，系统(1)至少存在4个不同的ω-正周期解。证毕。

3 举例

例1考虑以下非自治浮游生物竞争系统存在多个正周期解。

(16)

这里：

利用MATLAB软件计算，可得：

通过以上分析可知，定理1中的条件(H1)和(H2)成立。因此，由定理1可知，生物系统(16)至少存在4个不同的正周期解，周期为2。

4 总结

我们通过使用微分不等式技巧和Mawhin连续定理，获得离散型非自治浮游生物系统(1)至少存在4个不同正周期解的充分条件。由定理1的证明过程可知，如果系统(1)中h1(k)=h2(k)≡0，我们只能获得系统(1)存在1个正周期解，由于我们无法得到4个不同的Ωi(i=1,2,3,4)，且满足Ωi∩Ωj=φ(i≠j,i,j=1,2,3,4)。因此，在离散生态系统中，增加收获项h(k)会影响其多个周期变化规则和局部稳定的周期现象。