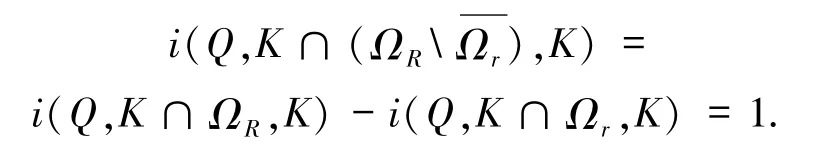李小龙

（陇东学院数学与统计学院，甘肃庆阳745000）

0 引言

分数阶微分方程在自然科学、工程技术和控制系统等领域有着广泛的应用，近年来许多学者应用相关的不动点定理与上下解的单调迭代技巧研究了分数阶边值问题的正解及其多个正解的存在性[1-10]，但在一般的Banach空间中对该类问题的研究还比较少.

设E为有序Banach空间，其正元锥P为正规锥，正规常数为 N，记 I=[0，1].本文将在一般的有序Banach空间E中讨论非线性分数阶边值问题

Banach空间的微分方程与普通微分方程的最大差异是把微分方程转换为与之等价的积分方程后，相应的积分算子不再具有紧性.为了对该积分算子应用凝聚映射的不动点定理，通常需要给非线性项f附加一些非紧性测度条件.本文使用了如下非紧性测度条件：

（H0）对∀R ＞0，f（I× PR）有界，且存在常数使得对∀t∈I，D⊂PR，有α（f（t，D））≤Lα（D），其中，Γ（·）为 Gamma函数，

在研究Banach空间中微分方程正解的文献中，文献[7]要求f在有界集上一致连续.文献[11]利用新的非紧性测度估计技巧，只在f连续的情形下获得了问题（1）的正解，并将文献[8]的结果推广到了无穷维空间.

1 预备知识

定义1[1]设 α ＞0，函数 f：（0，+∞）→R 的 α阶Riemann-Liouville积分为

其中Γ（·）为Gamma函数.

定义2[1]设 α ＞0，函数 f：（0，+∞）→R 的 α阶Riemann-Liouville导数为

其中，Γ（·）为 Gamma函数，n=[α]+1.

由Riemann-Liouville型微分的定义，有以下讨论.

引理1[1]设 α ＞0，假设 u∈C（0，1）∩L（0，1）是分数阶微分方程的解，则 u（t）具有如下形式，ci∈R，i=1，2，…，N，其中 N 是大于或等于 α 的最小正整数.

引理2[1]假设 u∈C（0，1）∩L（0，1）有 α ＞0阶导数属于 C（0，1）∩L（0，1），则

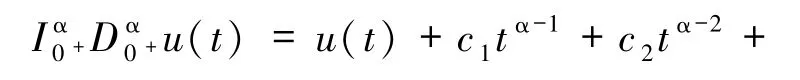
其中N是大于或等于α的最小正整数.

引理3[2]设 3 ＜ α≤4，则对∀h∈C（I，E），Banach空间E中的线性分数阶边值问题

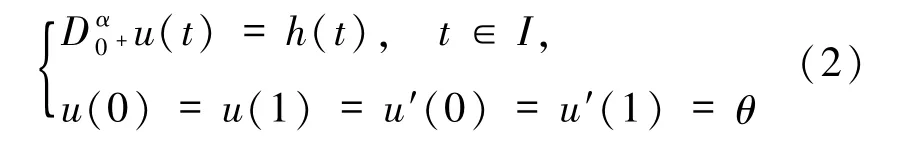
存在唯一解

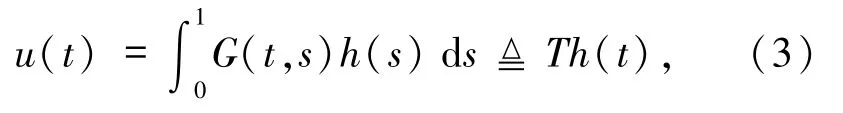
其中

引理4由（3）式定义的算子 T：C（I，E）→C（I，E）满足.

证明由（3）式知

故

从而

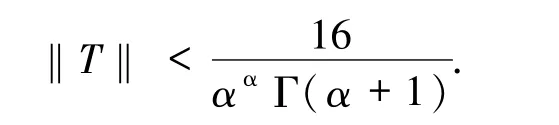
由文献[7]中引理3.2 知，算子 T：C（I，E）→C（I，E）为正的线性连续算子，T有相应第一特征值λ1的正特征函数 u*，即 λ1Tu*=u*.文中 E与C（I，E）中有界集的 Kuratiwski非紧性测度均由α（·）表示.对 B⊂C（I，E），记 B（t）=｛u（t）｜u∈B｝⊂E，t∈I.

引理5[12]设 B⊂C（I，E）为等度连续的有界函数族，则α（B（t））在I上连续，且

引理6[13]设 B=｛un｝⊂C（I，E）为可列集，若存在 ψ∈L1（I）使得‖un（t）‖≤ψ（t），a.e.，t∈I，n=1，2，…，则 α（B（t））在 I上可积，且

引理7[11]设D⊂E有界，则存在D的可列子集 D0，使得 α（D）≤2α（D0）.

定义算子 Q：C（I，P）→C（I，P）如下：

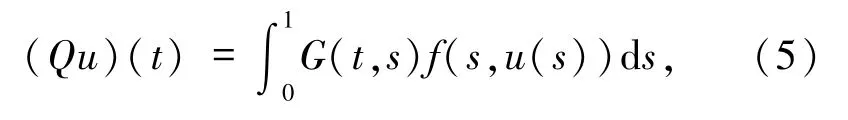
则 Q：C（I，P）→C（I，P）连续，且方程（1）的解等价于积分算子Q的不动点.

引理8设 f：I×P→P 满足（H0），则由（5）式定义的算子 Q：C（I，P）→C（I，P）为凝聚映射.

证明易见Q把C（I，P）中的有界集映为有界的等度连续集.任取非相对紧的有界集B⊂C（I，P），下证 α（Q（B））＜α（B）.令 R=sup｛‖u‖｜u∈B｝，则对 ∀t∈I，B （t）⊂ PR，设为假设（H0）中的非紧性测度常数.由引理7知，存在可列集 B1=｛un｝⊂B，使得α（Q（B））≤2α（Q（B1））.故对∀t∈I，由引理6 及假设（H0），有

因为Q（B1）等度连续，由引理5知

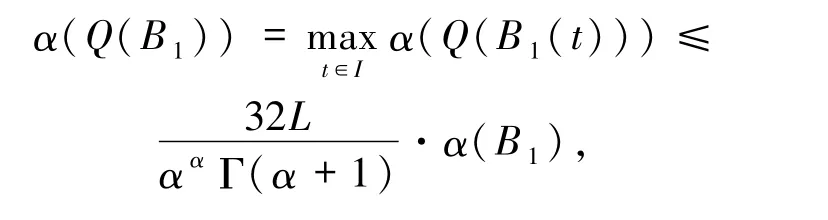
于是有

因此 Q：C（I，P）→C（I，P）为凝聚映射.

取 C（I，P）的子锥：

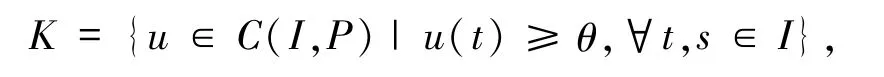
易证 Q（C（I，P））⊂K.因此，当 f：I× P→P 时，Q：K→K为凝聚映射，方程（1）的正解等价于Q在K中的不动点.本文将用凝聚映射的不动点指数理论寻找Q的不动点.

引理9[14]设E为Banach空间，K为E中的锥，Ω⊂E 为有界开集，θ∈Ω，Q：K∩→K 为凝聚映射，若 Q 满足 u≠λQu，∀u∈K∩∂Ω，0 ＜ λ≤1，则不动点指数 i（Q，K∩Ω，K）=1.

引理10[15]设E为Banach空间，K为E中的锥，Ω⊂E为有界开集，Q：K∩→K为凝聚映射，若存在 υ0∈K，υ0≠θ，使得 Q 满足 u-Qu≠μυ0，∀u∈K∩∂Ω，μ≥0，则不动点指数 i（Q，K∩Ω，K）=0.

2 主要结果及其证明

定理1设E为有序Banach空间，其正元锥P为正规锥，f：I×P→P 连续，满足条件（H0）.若 f满足下列条件之一：

（H1）1）存在及δ＞0，使得当 x∈Pδ时，f（t，x）≤εx；

2）存在 η ＞λ1及 h0∈C（I，P），使得当 x∈P时，f（t，x）≥ηx-h0（t）.

（H2）1）存在 ε ＞λ1及 δ＞0，使得当 x∈Pδ时，f（t，x）≥εx；

则边值问题（1）至少存在一个正解.

证明下证由（5）式定义的凝聚映射Q：K→K存在非零的不动点.取0＜r＜R＜∞，记Ωr=｛u∈K｜‖u‖ ＜r｝，∂Ωr=｛u∈K｜‖u‖ =r｝.分2 种情形证明当r充分小R充分大时Q在上存在不动点.

情形1f满足假设（H1）.取0＜r＜ δ，其中 δ为假设（H1）中的常数，证明Q满足引理9中条件：

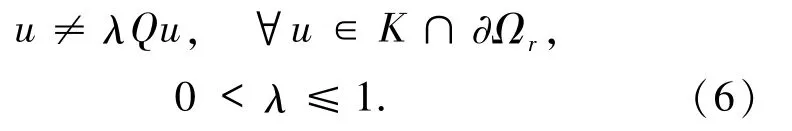
反设（6）式不成立，那么存在 u0∈K∩∂Ωr及 0＜λ0≤1，使得 u0=λ0Qu0.按 Q 的定义及条件（H1）的1）得

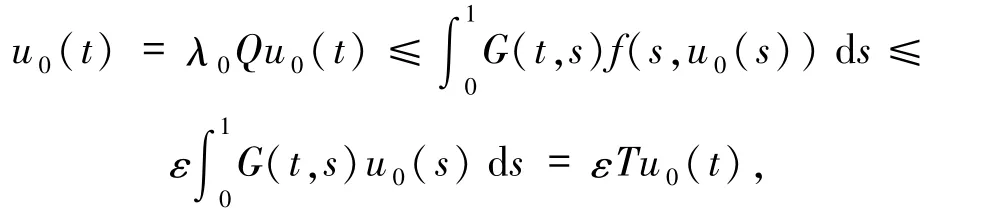
累次使用上式，则有

由锥K的正规性和引理4有

故有‖u0‖ =0，这与 u0∈K∩∂Ωr（‖u0‖ =r）矛盾.于是（6）式成立，故由引理9知

下证当R充分大时有

反设存在 u0∈K∩∂ΩR及 τ0≥0，使得 u0-Qu0=τ0u*，则按算子Q的定义及条件（H1）的2）得

从而有

又 η ＞λ1知（ηT-I）为正算子，故逆算子（ηTI）-1存在，由锥K的正规性得

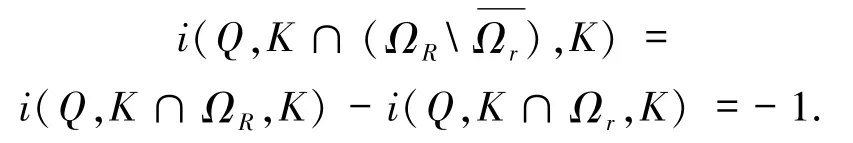
情形2f满足假设（H2）.取0 ＜r＜δ，证明

反设（10）式不成立，则存在 u0∈K∩∂Ωr及 τ0≥0，使得u0-Qu0=τ0u*，则u0=Qu0+τ0u*≥τ0u*，令，即，且 u0≥ τ*u*.又由 T的正性知，λ1Tu0≥τ*λ1Tu*=τ*u*.

由条件（H2）的1）有

这与τ*的定义矛盾.故由引理10知

再证当R充分大时有

假设存在u0∈K及0＜λ0≤1，使得u0=λ0Qu0.

从而由条件（H2）的2）得

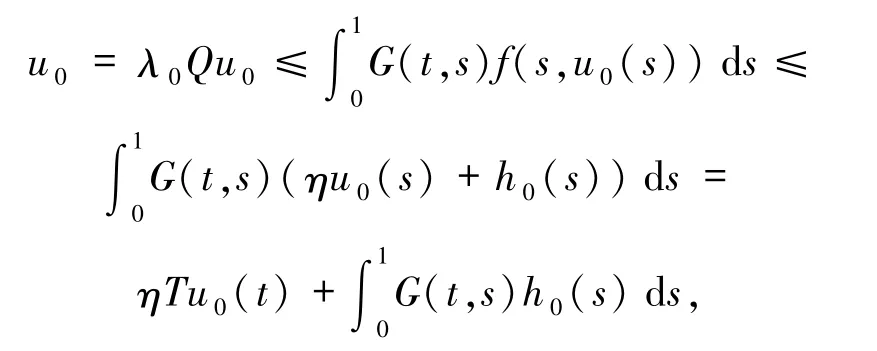
即

又

则

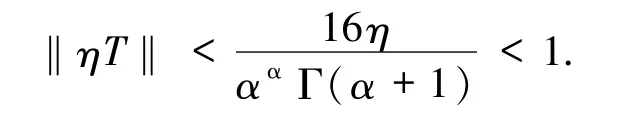
由微扰定理知，I-ηT存在有界逆算子（I-ηT）-1，且

从而由锥K的正规性得

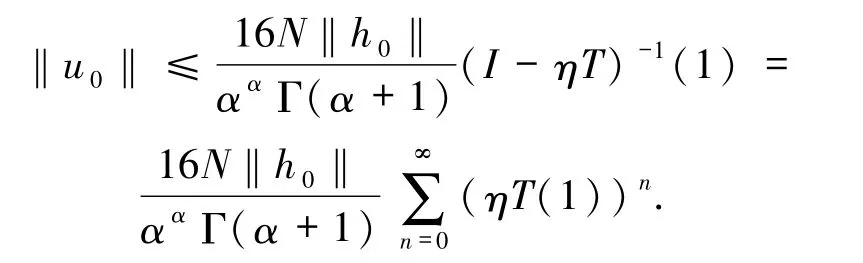
取 ε0＞0，使得

则有

则有

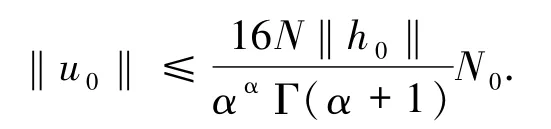
由引理9知 i（Q，K∩ΩR，K）=1，于是该式结合（11）式有