曾 庄，黄天民，赵庆庆，徐 颖

（西南交通大学数学学院，四川成都611756）

1965年，美国控制论专家Zadeh[1]提出了模糊集（FS）的概念，将数学的研究范围从精确问题拓展到了模糊问题.1986年，Atanassov[2]提出了直觉模糊集（IFS），直觉模糊集从支持、反对、中立3个方面全面地描述了客观世界，直觉模糊集在处理模糊性和不确定性等方面比模糊集更具有灵活性和实用性，是模糊集的推广.在过去的几十年里，很多学者对其进行了深入的研究，并将直觉模糊集广泛应用于各种领域，其中关于直觉模糊决策的研究是热点问题，如多属性决策（MADM）[3]和多属性群决策（MAGDM）[4].

随着研究的深入，一些学者发现直觉模糊集也存在着一些缺陷.在决策过程中，假设决策者对某事物支持的程度是，而反对的程度是，支持与反对程度的和超过1，这时与直觉模糊集的约束条件：隶属度与非隶属度之和小于1相矛盾.为此在研究模糊集和直觉模糊集的补运算基础上，2014年，Yager[5]通过定义毕达哥拉斯模糊补运算，提出了允许隶属度和非隶属之和超过1，而它的平方和不超过1的毕达哥拉斯模糊集的概念，毕达哥拉斯模糊集比直觉模糊集具有更强的刻画模糊现象的能力，是直觉模糊集的推广.最近几年，很多文献研究了毕达哥拉斯模糊集，Yager[5]和 Yager 等[6]提出了毕达哥拉斯隶属度的自然拟序，Zhang等[7]提出了毕达哥拉斯模糊数（PFN）的概念，定义了一种记分函数，研究了基于毕达哥拉斯模糊集的TOPSIS方法及其应用.Zhang[8]提出了毕达哥拉斯模糊数的严格排序，定义了毕达哥拉斯模糊数的相似性度量，提出了一种简单有效的毕达哥拉斯多属性决策方法.Peng等[9]定义了减法和除法运算，提出了精度函数，提出了毕达哥拉斯模糊数的排序方法.Liang 等[10]和 Peng 等[11]研究了区间值毕达哥拉斯模糊集及其决策应用.Gou等[12]研究了毕达哥拉斯模糊数的连续性及微分等内容；Garg[13]研究了基于Einstein的广义毕达哥拉斯模糊信息聚合算子及其在决策中的应用；刘卫锋等[14]研究了毕达哥拉斯模糊交叉影响集成算子及其决策应用；刘卫锋等[15]研究了毕达哥拉斯模糊Hamacher集成算子及其决策应用.

从目前的毕达哥拉斯模糊数排序方法来看，似乎在解决毕达哥拉斯模糊环境下的多属性决策问题等方面是有效的，但是也存在着某些不足.文献[7-8]利用记分函数和精度函数对毕达哥拉斯模糊数进行排序，仅仅涉及到隶属度和非隶属度的信息，而忽略了犹豫度的作用.因为在决策过程中存在着固有信息的丢失，使得有时候这些方法的排名结果可能不准确.在文献[16]提出的新的记分函数的基础上，本文首先定义了一种新的记分函数和精确度函数，然后提出了相应的排序方法，该方法不仅充分考虑了隶属度、非隶属度、犹豫度三方面的信息，还比文献[7-8]的方法更直接有效，也比文献[16]的方法简便.然后在分析文献[15]提出的毕达哥拉斯模糊Hamacher运算时，发现该运算没有考虑不同毕达哥拉斯模糊数的隶属度和非隶属度之间存在着某种关联和相互影响.因此，本文在毕达哥拉斯模糊交叉影响集成算子[14]启发下，定义了毕达哥拉斯模糊数的加法、数乘、乘法以及幂运算并研究了它们的一些性质，给出了相应的证明.

1 基础知识

1.1 直觉模糊集

定义1[2]设 X 为论域，A=｛〈x，μA（x），νA（x）〉｜0≤μA（x）+νA（x）≤1，x∈X｝称为 X 上的一个直觉模糊集（IPS），其中 μA（x）：X→[0，1]，νA（x）：X→[0，1]是 X 上的模糊集，μA（x）、νA（x）分别表示X上元素x属于A的隶属度和非隶属度.

1.2 毕达哥拉斯模糊集

定义2[5]设X 为论域，则称三元组为毕达哥拉斯模糊集（PFS），其中 μA（x）：X→[0，1]，νA（x）：X→[0，1]是 X 上的模糊集，μA（x）、νA（x）分别表示X上元素x属于A的隶属度和非隶属度，并且∀x∈X，μA（x），νA（x）∈[0，1]，

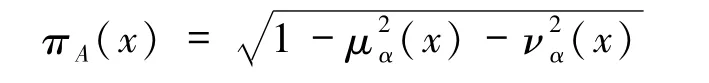
为x隶属于A的犹豫度.为了简便，称α=（μα（x），να（x））为毕达哥拉斯模糊数（PFN）[7]，表示为 α =（μα，να）.

毕达哥拉斯模糊集是直觉模糊集的推广，并且比直觉模糊集具有更强的刻画模糊现象的能力.

2 毕达哥拉斯模糊数的记分函数和精度函数

2.1 记分函数和精度函数

定义3[7]设 α =（μα，να）为毕达哥拉斯模糊数，则 α 的记分函数定义为，其中S（α）∈[-1，1].α 的精度函数定义为 A（α）=，其中 A（α）∈[0，1].

设 α1=（μα1，να1），α2=（μα2，να2）为 2 个毕达哥拉斯模糊数，分别是 α （i=1，2）的记分函数和精度函i数，比较方法如下：

（i）若 S（α1）＜S（α2），那么 α1＜α2；

（ii）若 S（α1）=S（α2），那么：

（a）若 A（α1）＜A（α2），那么 α1＜α2，

（b）若 A′（α1）=A′（α2），那么 α1～α2.

2.2 毕达哥拉斯模糊数新的记分函数和精度函数针对文献[7]所提方法存在的不足，以及结合文献[16]提出的记分函数、有效函数应充分考虑支持者、异议者和弃权者的份额，定义一种新的记分函数，它具有较强的选择能力和较高的精确度.

定义4设 α=（μα，να）为毕达哥拉斯模糊数，定义α的记分函数为

并且 S′（α）∈[-1，1].

相应地可以定义一种新的精度函数如下：

定义5设 α=（μα，να）为毕达哥拉斯模糊数，那么α的精度函数为

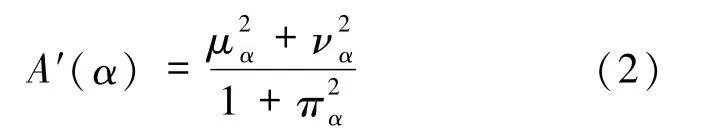
并且 A′（α）∈[0，1].

可以发现，当 S′（α）、A′（α）越大，相应的毕达哥拉斯模糊数就越满足决策者的期望.在此基础上可以得到毕达哥拉斯模糊数的一种新的排序方法：

定义6设 α1=（μα1，να1），α2=（μα2，να2）为2个毕达哥拉斯模糊数，且

分别是αi（i=1，2）的记分函数和精度函数，比较方法如下：

（i）若 S′（α1）＜ S′（α2），那么 α1＜ α2；

（ii）若 S′（α1）=S′（α2），那么：

（a）若 A′（α1）＜A′（α2），那么 α1＜α2，

（b）若 A′（α1）=A′（α2），那么 α1～α2.

定理1对于任意的毕达哥拉斯模糊数α=（μα，να），记分函数是关于隶属度μα的单调增函数，是关于非隶属度να的单调减函数.

证明由于

其中 μα，να∈[0，1]，记分函数分别对隶属度 μα和非隶属度να求偏导：

同理

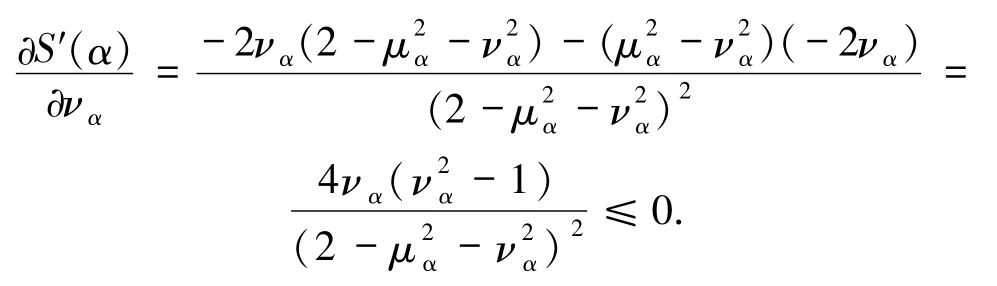
因此，可得 S′（α）是关于隶属度 μα的单调增函数，是关于非隶属度να的单调减函数.

定理2设 α1=（μα1，να1）和 α2=（μα2，να2）为任意2 个毕达哥拉斯模糊数，当 S（α1）=S（α2），且 A（α1）＞A（α2），有 S′（α1）＞S′（α2）.

证明由于 S（α1）=S（α2），且 A（α1）＞A（α2），所以有

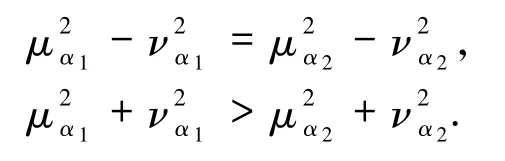
从而

所以结论成立.

该定理说明新的排序方法对旧的排序方法进行了改进，比旧的排序方法更直接有效，并且吸收了更多的模糊信息.

例1设有毕达哥拉斯模糊数：

那么由定义3所得的排序方法可知：

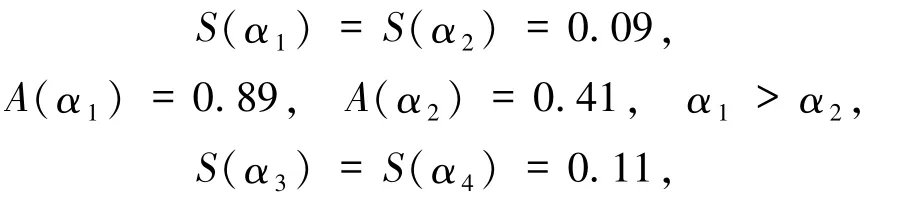
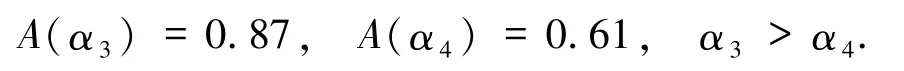
此时无法直接用记分函数判断毕达哥拉斯模糊数的大小，还需要借助精度函数进行排序.

而由定义6所得的排序方法可知：

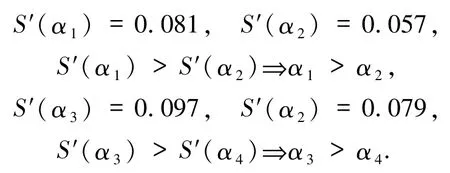
也就是说，当定义3的得分函数不能直接对毕达哥拉斯模糊数进行排序时，但是定义4所提出的得分函数可以区分备选方案的差异，发现最终结果相同.这意味着提出的得分函数是直截了当并且有效的.

例2毕达哥拉斯模糊数 α1=（0.3，0.9），，那么由定义3所得的排序方法可知：

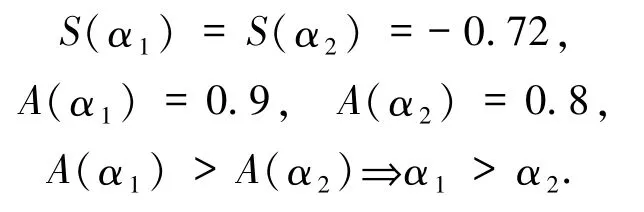
但是如果对模糊数α1进行一点点修改为

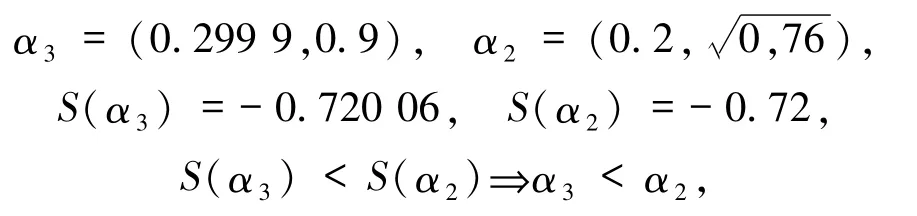
排序结果却截然不同.

而由定义6的排序方法可知：

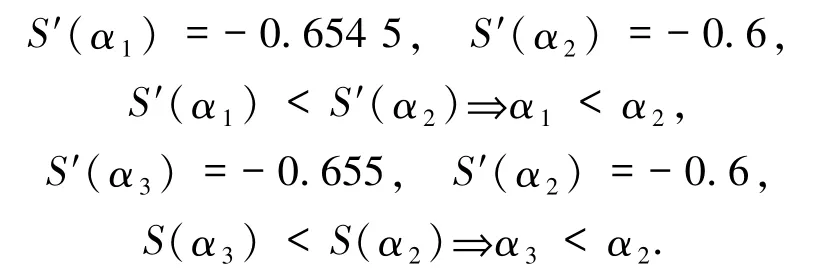
所以当隶属度只有0.000 1的变化时，定义3的排序方法得到的却是完全相反的排序结果.说明在比较的过程中，仅仅考虑隶属度和非隶属度而忽略犹豫度，会丢掉一些有用的信息，使得结果存在着偏差.但是定义6的排序方法却不会受影响.说明本文提出的新排序方法比旧排序方法更稳定，更易于实现.

3 毕达哥拉斯模糊数运算法则与性质

本节将介绍毕达哥拉斯Einstein运算[13]和毕达哥拉斯交叉影响运算[14]，然后提出一种毕达哥拉斯模糊数新的运算法则和相应的运算性质.

3.1 毕达哥拉斯模糊Einstein运算法则

定义7[13]设 α =（μα，να）和 αi=（μαi，ναi）（i=1，2）为任意3个毕达哥拉斯模糊数，λ≥0，那么毕达哥拉斯模糊Einstein运算定义如下：

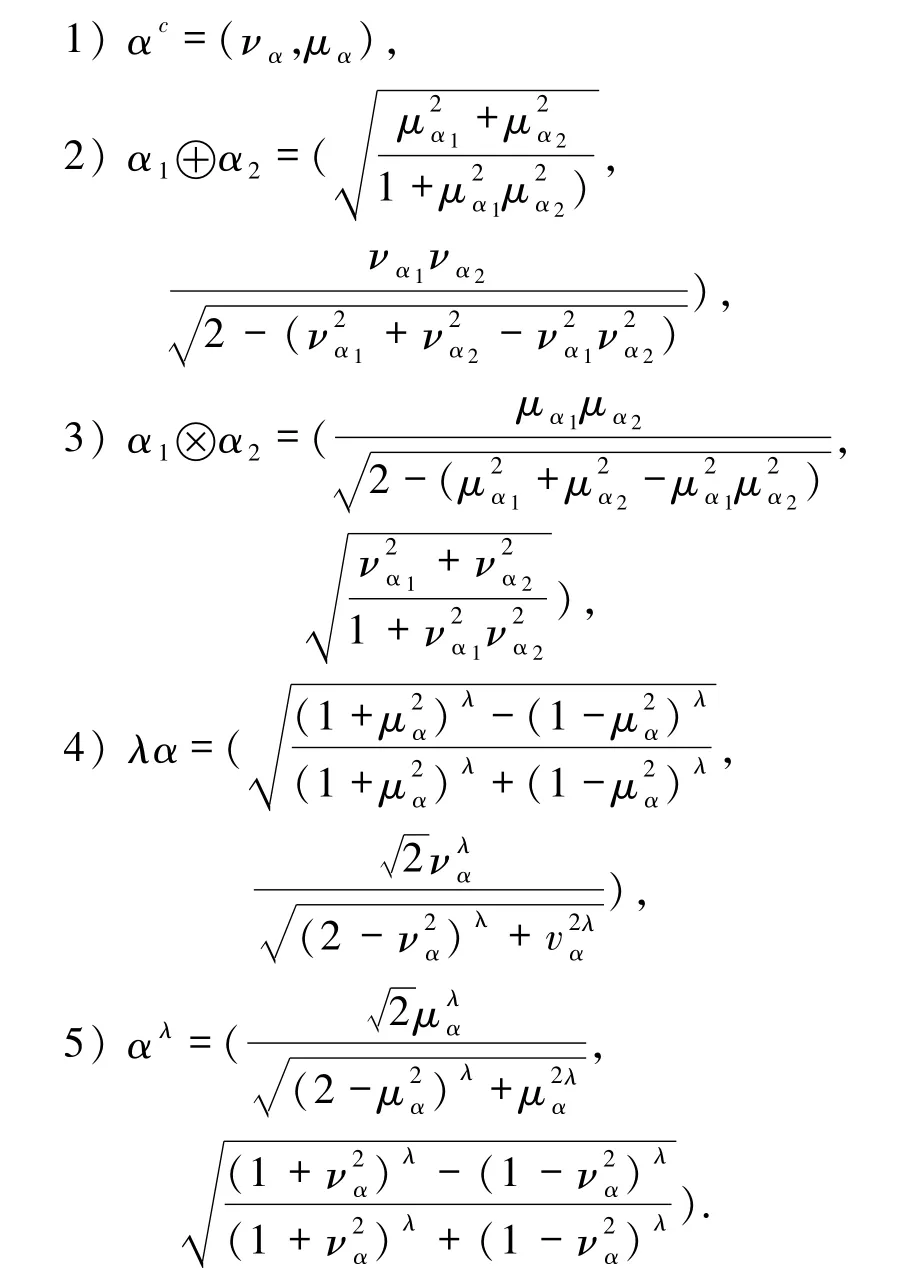
例3设 α1=（μα1，0），α2=（μα2，να2），να2≠0为毕达哥拉斯模糊数，那么由定义7的加法运算可知：

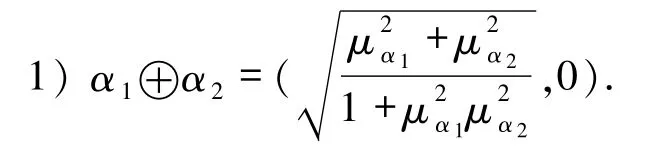
设 α3=（0，να3），α4=（μα4，να4），μα4≠0 为毕达哥拉斯模糊数，那么由定义7的乘法运算可知：

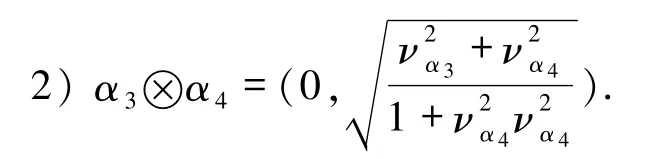
即在上述运算中 να2、μα4完全不起作用，也显然与常理不符，基于这种缺陷，刘卫锋等[14]定义了新毕达哥拉斯模糊数的加法、乘法、数乘以及幂运算.

定义8[14]设 α =（μα，να）和 αi=（μαi，ναi）（i=1，2）为任意3个毕达哥拉斯模糊数，并且λ≥0，那么毕达哥拉斯模糊交叉影响运算定义如下：

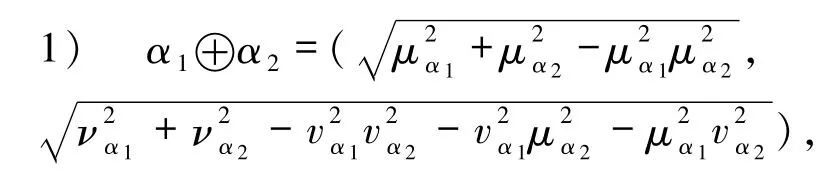
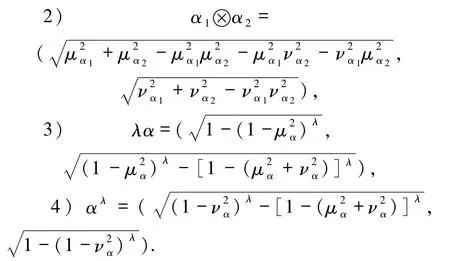
定义8考虑到不同的毕达哥拉斯数的隶属度和非隶属度之间存在着某种联系和相互影响，一定程度上避免了例3中存在的这种缺点.

3.2 毕达哥拉斯模糊数新的运算法则在定义7和8的启发下，本文结合以上2种毕达哥拉斯模糊数运算，充分地将毕达哥拉斯Einstein运算和毕达哥拉斯模糊交叉影响运算的优点联合起来，提出了以下毕达哥拉斯模糊数新的运算，并给出了相应的证明.

定义9设 α =（μα，να）和 αi=（μαi，ναi）（i=1，2）为任意3个毕达哥拉斯模糊数，并且λ≥0，那么毕达哥拉斯模糊数运算定义如下：

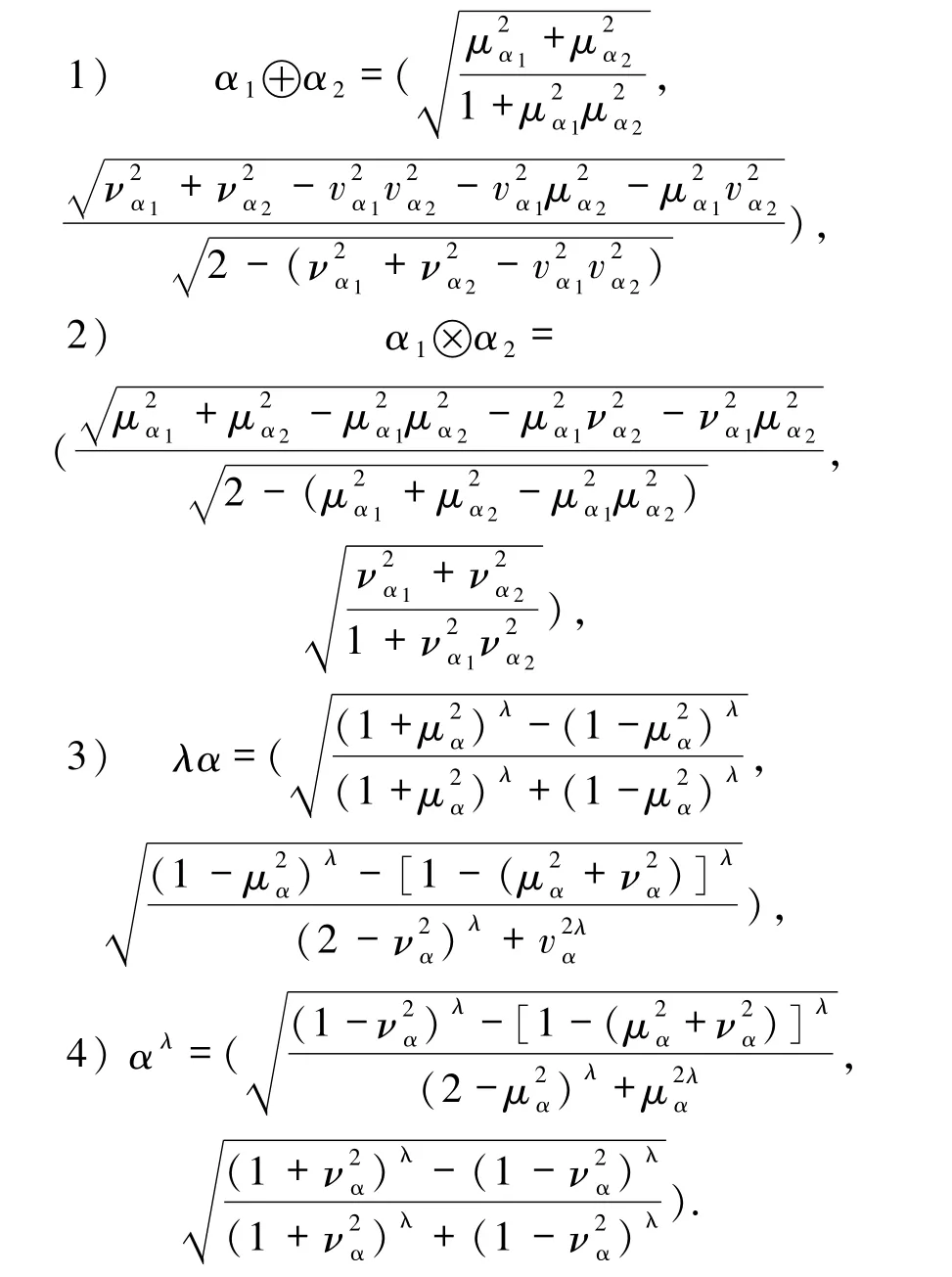
例4设 α1=（μα1，0），α2=（μα2，να2），να2≠0为毕达哥拉斯模糊数，那么由定义9的加法运算可知：

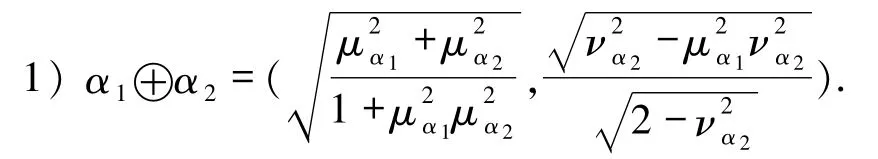
设 α3=（0，να3），α4=（μα4，να4），μα4≠0 为毕达哥拉斯模糊数，那么由定义9的乘法运算可知：

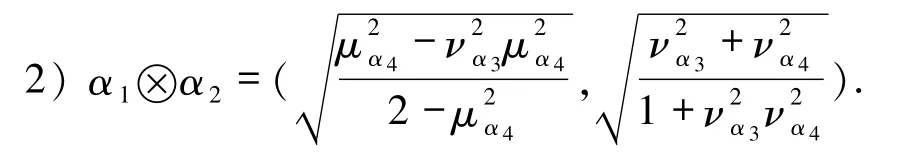
显然在上面的运算结果比定义7得到的结果吸收的模糊信息更多，更符合实际.

3.3 毕达哥拉斯模糊数新的运算性质

定理3设 α =（μα，να）和 αi=（μαi，ναi）（i=1，2）为任意3个毕达哥拉斯模糊数，并且λ≥0，则定义8的毕达哥拉斯模糊数运算α1⊕α2、α1⊗α2、λα、αλ也是毕达哥拉斯模糊数.

证明1）证明α1⊕α2是毕达哥拉斯模糊数，从而需要证明

2）α1⊗α2是毕达哥拉斯模糊数的证明与1）类似.这里不再证明.

3）证明λα是毕达哥拉斯模糊数，从而需要证明

4）αλ是毕达哥拉斯模糊数的证明与3）类似.这里不再证明.

定理4设 α =（μα，να）和 αi=（μαi，ναi）（i=1，2）为任意3 个毕达哥拉斯模糊数，λ，λ1，λ2≥0，则毕达哥拉斯模糊数运算满足：

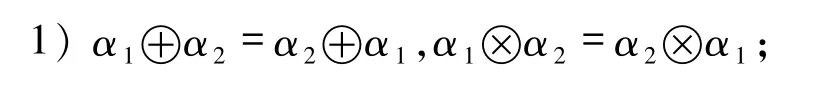
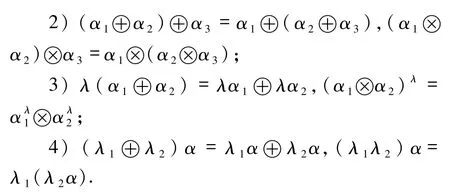
定理5设 αi=（μαi，ναi）（i=1，2）为任意 2个毕达哥拉斯模糊数，则毕达哥拉斯模糊数运算满足：

4 结束语

考虑到目前记分函数和精度函数缺陷的基础上，本文提出了新的记分函数和精度函数，以及得到了相应的毕达哥拉斯模糊数排序方法.该方法的优点在于：1）同时考虑了隶属度、非隶属度、犹豫度三方面的信息，在决策过程中可以吸收更多的模糊信息；2）比起文献[16]的计算公式里面有指数函数运算，本文的计算公式更简便且易于实现.然后定义了毕达哥拉斯模糊数的一种新的运算法则以及得到了相应的性质.本文的研究使得毕达哥拉斯模糊运算更加符合实际，为毕达哥拉斯模糊数的进一步研究奠定基础.