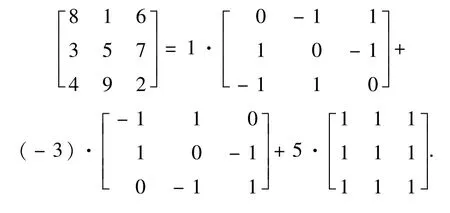赵世恩 刘效丽

(首都师范大学初等教育学院，北京 100048)

0 引 言

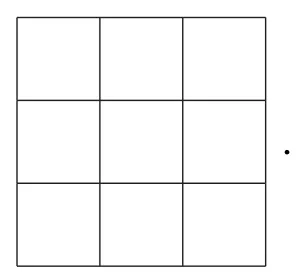
对于经典的九宫格，要求将1，2，3，4，5，6，7，8，9这9个数字填入下面的九宫格，并且满足纵向、横向、斜向3个数的和均等于15.

对于九宫格，主要涉及以下2个问题:

问题1给定9个数，如何将其填入九宫格.

问题2如何构造纵向、横向、斜向3个数的和皆相等的9个数.

本文利用高等代数中的线性方程组理论[1]，明确的给出了上面2个问题的答案.具体地说，讨论的前提是去掉“填入 1，2，3，4，5，6，7，8，9 这 9 个数”以及“3个数的和皆等于15”的限制，只要求纵向、横向、斜向3个数的和相等.在这个条件下，首先给出九宫格解的定义并建立九宫格解的2个必要条件；其次，根据这2个必要条件，讨论九宫格的一般填法；最后，利用线性方程组理论给出九宫格解的一般表达式.

首先介绍一些基本概念.

定义 0.1设x1，x2，...，x9，k∈R，将x1，x2，…，x99个数依次填入如下九宫格当中:

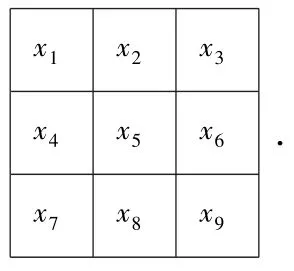
如果满足每行元素之和、每列元素之和以及2条对角线元素之和都等于k，则称x1，x2，…，x9满足Δ(k)条件，也称x1，x2，…，x9，k为九宫格的1个解.

例1对于熟知的九宫格，

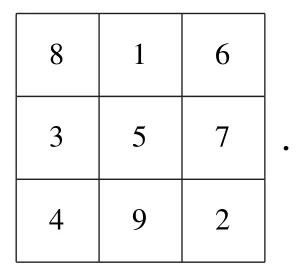
根据定义0.1，称8，1，6，3，5，7，4，9，2满足Δ(15)条件，或称8，1，6，3，5，7，4，9，2，15是九宫格的1个解.

定义0.2若将x1，x2，…，x99个数依次填入九宫格，如定义1所示，称:

(1)x1，x3，x7，x9所在位置为九宫格的角；

(2)x2，x4，x6，x8所在位置为九宫格的边；

(3)x5所在位置为九宫格的中心，x5为中心元；

(4)x1和x3所在位置为邻角，x1和x9所在位置为对角；

(5)x2和x4所在位置为邻边，x2和x8所在位置为对边；

(6)x1，x2，…，x99个数中最大的元素和最小的元素分别为九宫格的最大元和最小元.

本文的框架如下:第1节，讨论了九宫格解的2个必要条件；第2节，在得到必要条件的基础上，讨论了九宫格的一般填法；第3节，给出了九宫格解的一般表达式.

1 九宫格解的2个必要条件

命题 1.1设x1，x2，…，x9满足Δ(k)条件，l∈R.则:

(1)lx1，lx2，…，lx9满足Δ(lk)条件；

(2)x1+l，x2+l，…，x9+l满足Δ(k+3l)条件.

事实上，如果x1，x2，…，x9满足Δ(k)条件，则它们满足如下齐次线性方程组:

令A为上述方程组的系数矩阵，x=(x1x2x3x4x5x6x7x8x9k)′，则上述方程组可以写作:Ax=0.令ai表示矩阵A的第i列，i=1，2，…，9，容易看到ai就是xi的系数构成的列向量.

下面计算矩阵A的秩.利用Matlab软件[2]，将A化为简化阶梯形矩阵:

得到A的秩为7.由线性方程组理论，可以得到如下定理:

定理1.1方程组(1)的自由变量个数为3，即九宫格的解构成了10维线性空间中的一个3维子空间.

另外，从矩阵(3)的第5行，得到:

定理1.2如果x1，x2，…，x9满足Δ(k)条件.则3x5=k.

此结论给出了九宫格解的一个必要条件.

注1.1根据命题 1.1，对于九宫格的一个解，对其进行平移之后仍是九宫格的解，因此不妨设k=0.本文，在没有特别强调的情况下，均假设k=0.此时，根据定理1.1和1.2，由于k和x5已知，方程组(1)的自由变量个数为2，即九宫格的解构成了8维线性空间中的一个2维子空间.

通过观察例1可以看出，相邻两边上的元素之和等于它们所对的角上元素的2倍.下面只证明2x1=x6+x8，令其中m=(-1-1-1-1-1-1-1-1)′为k的系数.利用Matlab软件，将B化为简化阶梯形矩阵如下:

根据矩阵(4)中的第7行，可以得到九宫格解的另一个必要条件:

定理 1.3如果x1，x2，…，x9满足Δ(k)条件，则2x1=x6+x8.进一步，根据九宫格的对称性，有2x3=x4+x8，2x7=x2+x6以及2x9=x2+x4.

注1.2由必要条件定理1.2和1.3，可以得出很多有用的结论.为了第2节讨论的方便，这里先给出2个推论，由于证明很简单，这里不再赘述.

推论1.1若九宫格中有1组对边或1组对角上的元素都是最大元，则九宫格上的所有元素都是最大元.

推论1.2若九宫格中角上的元素是最大元，当且仅当与其不相邻的2个边上的元素也是最大元.

注1.3根据上面的2个推论，不难看出最小元也有类似的结论.

2 九宫格的一般填法

事实上，可以从九宫格的最大元开始填起.设Λ表示y1，y2，…，y9中最大元构成的集合.

首先，由于考虑的数域是实数，因此Λ不是空集；

其次，对于集合Λ，有如下3个断言.

断言2.1Λ中不可能只有2个元素.由推论1.1和1.2便可得知.

断言2.2若Λ中含有3个元素，根据推论1.1和1.2以及注1.3，该九宫格一定有如下形式

断言2.3若Λ中元素的个数大于3，则y1=y2=…=y9.

不妨设y6，y7，y8以及y9均属于Λ，下面分如下2种情形来讨论:

情形1，九宫格角上没有y6，y7，y8以及y9这4个数，即这4个元都在边上，

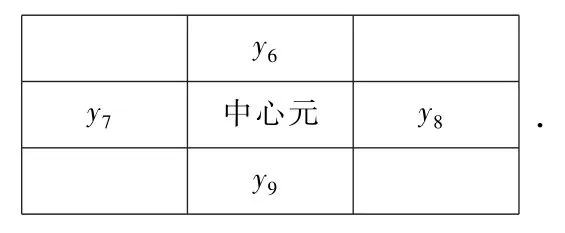
则根据推论1.1，有y1=y2=…=y9；

情形2，若九宫格角上至少有y6，y7，y8以及y9中的一个元，则根据定理1.3，可以得到如下形式

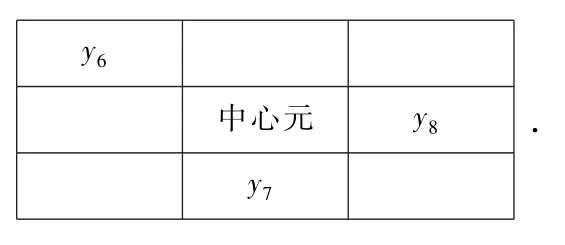
此时y9无论在什么位置，由推论1.1，有y1=y2=…=y9.

注2.1根据上面的讨论，集合Λ中含有元素的个数只有1，3或9这3种可能，而且只须讨论Λ中只含有1个元素的填法.

下面，给出九宫格具体的填法.

设y1，y2，…，y9是任意给定的9个实数，满足Δ(k)条件且Λ={y9}.

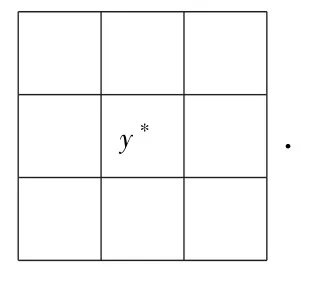
第一步:根据定理 1.2，y1，y2，…，y9中一定存在一个元等于这9个数的算术平均，不妨设为y∗.所在的位置一定是九宫格的中心.此时，九宫格如下:

第二步:根据推论1.2，最大元y9不可能在角的位置.因此y9所在的位置一定是边，不妨设九宫格如下:

第三步:假设剩下元素中的最大元有y8，

(1)如果y8在如下位置，

则y8+y∗+y9＞3y∗，根据定理1.2这是不可能的；

(2)由定理1.3，y8和y9不能在相邻的边；

(3)y8和y9不能相邻，不妨设九宫格如下:

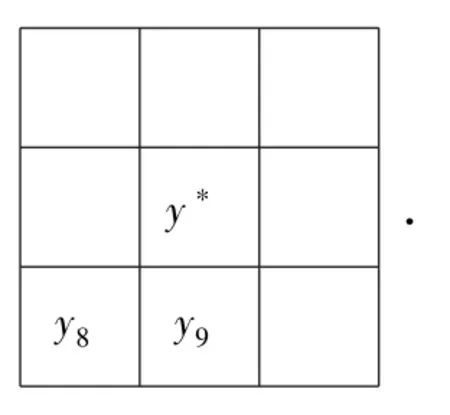
观察下面的形式

其中y′和y″是y1，y2，…，y7中的2个元.根据九宫格解的定义，可以得到

这与y8和y9为y1，y2，…，y9中最大和次大的2个数矛盾；

因此y8的位置只能是如下2种可能:

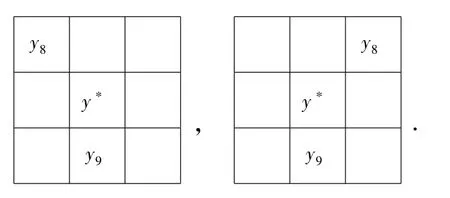
第四步:根据定理1.2和1.3，可以通过简单的计算，将y1，y2，…，y9剩下的元素填入九宫格.

注2.2经过上面的讨论，完全回答了引言中的问题1.事实上，还可以从最小元构成的集合开始讨论.由于方法是一样的，因此这里不再论述.

3 九宫格解的一般结构

在已知k=0的情况下讨论.根据线性方程组(1)，系数矩阵A可以简化为

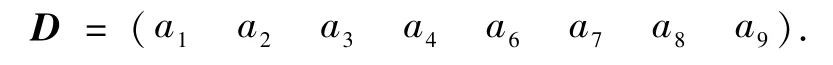
利用Matlab软件，将D化为简化阶梯形矩阵如下:

容易得到如下定理:

定理3.1九宫格相邻的角和边上的元素可以作为自由变量，若分别令

其中k1，k2为任意实数.如果将上面解的结构和九宫格每个元素的位置对应起来，则得到如下形式:

注3.1容易看到，式(6)右边的2个3×3矩阵是分别关于主对角线和副对角线反对称的形式，也恰恰是k=0时九宫格解空间的一组基底；进一步，对于k≠0的情况，将方程组(1)写成如下非齐次线性方程组的形式:

根据线性方程组理论，只需式(7)的导出组的基础解系加上它的一个特解，便可得到所有满足Δ(k)条件的解，即九宫格解的一般结构为:

其中k1，k2为任意实数.

由此，只要确定上面的k1，k2以及k，就能够构造出九宫格所有的解，这也就解决了引言中的问题2.事实上，对于例1中的九宫格，有如下表示形式: