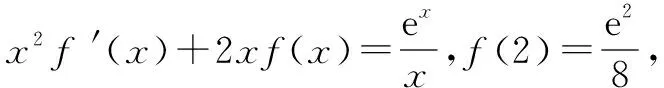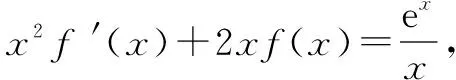“设而不求”思想在函数中的应用
2020-06-06喻秋生
喻秋生
(广东省深圳实验学校高中部 518055)
“设而不求”思想是数学解题中一种很有用的解题方法.所谓“设而不求”,顾名思义就是指在解题过程中根据需要设出变量,但是并不具体地去直接解出变量的值,而是利用某种关系去表示变量间的联系.采用设而不求的策略,往往能避免盲目推演而造成的无益的循环运算,从而达到准确、快速、简捷的解题效果.
我们知道,高中数学常用到“设而不求”思想的是解析几何,它能使很多解析几何问题得到简化.同样,“设而不求”的思想方法在处理函数问题中也有很重要的作用,下面谈谈“设而不求”思想方法在函数中的应用.
一、在函数最值问题中的应用
在研究函数最值问题时,有时会遇到给出的函数存在最值,但求不出或很难求出最值,这时可以应用“设而不求”思想,利用函数性质进行处理.

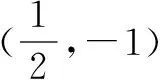
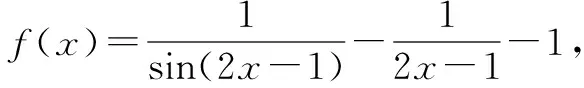

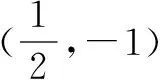
因此,假设函数f(x)的最大值为f(a),则f(x)的最小值为f(1-a),

∴M+m=-2.
二、在导函数隐零点问题中的应用
当导函数存在零点,但零点式子非常繁琐或无法求解时,可考虑虚设零点x0,再对零点进行合理的变形与代换,将超越式化为普通式,从而达到化简的目的.
例2 设f(x)=ex-x-2,若x>0时,不等式(x-k)f′(x)+x+1>0恒成立,求整数k的最大值.
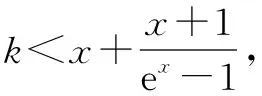
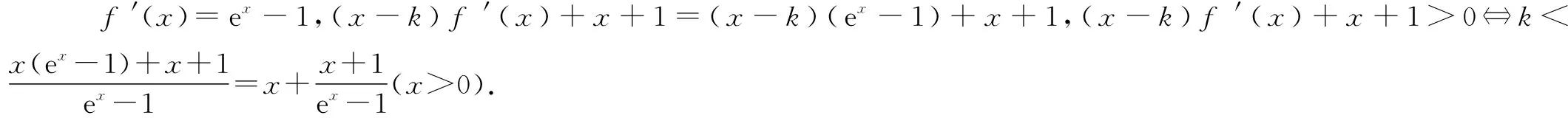
令h(x)=ex-x-2(x>0),则h′(x)=ex-1>0,
h(x)在(0,+)单调递增,且h(1)=e-3<0,h(2)=e2-4>0,
所以h(x)存在唯一的零点x0∈(1,2),由h(x0)=0⟹ex0=x0+2,
易得g(x)在(0,x0)单调递减,在(x0,+)单调递增,所以将ex0=x0+2代入,得g(x)min=x0+1∈(2,3),
又k 函数不等式的证明,一般是转化为最值与0比较,当函数的最值存在,但求不出具体的值时,可先用变量表示,再证明不等式成立. 例3 已知f(x)=e2x-m-ln(2x+1),当m≤1时,求证f(x)>0恒成立. 分析要证f(x)>0恒成立,即证f(x)的最小值大于0.由于f′(x)的零点不能直接求出,则可通过设零点为x0,用x0表示最小值,再证明最小值大于0. 由(*)式两边取对数,得ln(2x0+1)=m-2x0,………(**). 将(*)、(**)代入,得 所以,不等式f(x)>0恒成立. 在处理导数问题时,有时会遇到没有给出函数的表达式,但给出函数满足的条件,根据条件又不能直接求出函数解析式,这时可考虑“设而不求”这种解题方法. A.有极大值,无极小值 B.有极小值,无极大值 C.既有极大值又有极小值 D.既无极大值也无极小值 ∵当x>2时,h′(x)>0,当0 ∴当x>0时,h(x)≥h(2). 总之,“设而不求”这种思想就像一座桥梁,把未知与已知巧妙地联系在一起了,我们平时解题时如果遇到了一些不能回避的未知量,而题目所求的问题并不需要求出该未知量时,就可以尝试这种“设而不求”的方法,通过简化求解过程,使问题迎刃而解.三、在证明函数不等式中的应用
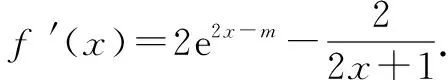
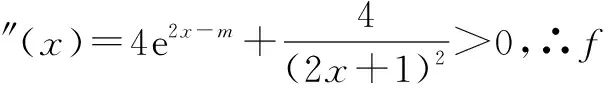
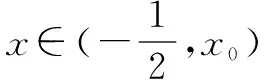
四、在隐函数问题中的应用