Yiqiang Q. Zhao

(School of Mathematics and Statistics, Carleton University, Ottawa, ON Canada K1S 5B6)

Abstract In this paper, we provide a review on the GTH algorithm, which is a numerically stable algorithm for computing stationary probabilities of a Markov chain. Mathematically the GTH algorithm is an rearrangement of Gaussian elimination, and therefore they are mathematically equivalent. All components in the GTH algorithm can be interpreted probabilistically based on the censoring concept and each elimination in the GTH algorithm leads to a censored Markov chain. The RG-factorization is a counterpart to the LU-decomposition for Gaussian elimination. The censored Markov chain can also be treated as an extended version of the GTH algorithm for a system consisting of infinitely many linear equations. The censored Markov chain produces a minimal error for approximating the original chain under the l1-norm.

Key words GTH method Gaussian elimination Markov chain Censored Markov chain RG-factorization Stationary probability Numerical stable algorithm

1 Introduction

Stationary probabilities are crucial for stationary behaviour of stochastic systems, which can be often modeled as a Markov chain. Explicit expressions for the stationary distribution are available for a small set of problems. In most of applications, simulation or numerical computations are main tools for a solution. Therefore, computational methods for Markov chains are very important. Algorithms are usually presented for a finite-state Markov chain, since computers can only deal with finite-many states. When using finite-state Markov chains to approximate an infinite-state Markov chain, convergence and the approximation error are among fundamental questions to answer.

The GTH algorithm discussed in this paper was proposed by Grassmann, Taksar and Heyman in 1985 [7]. Then, it became very attracted to many researchers. A list of publications by 1993, in which the GTH algorithm was used, can be found in Grassmann [5], including: Kohlas [14], Heyman [10], Heyman and Reeves [11], Grassmann and Heyman [6], Stewart [24], O’Cinneide [22]. The list of references closely related to the GTH algorithm, published after 1993, is so large, and only a small sample is included here: Stewart [25], Dayar and Stewart [2], Grassmann and Zhao [8], Sonin and Thornton [23], Dayar and Akar [1], Hunter [12]. Therein from the above publications, many more references can be found.

The GTH algorithm is a numerically stable version of Gaussian elimination, or a rearrangement of Gaussian elimination. Through the rearrangement, subtractions are avoided in the algorithm, which are often the reason causing computational instability. The rearrangement makes the elimination process start with the largest state that controls the error in computations. The GTH algorithm possesses a probabilistic interpretation. This interpretation becomes very clear in terms of the censoring concept of the Markov chain. Two important measures, the RG-measures, for Markov chains are invariant under the censoring Based on this property one can prove that the GTH algorithm is equivalent to the RG-factorization, which is a counterpart to the LU-decomposition for Gaussian elimination. The censored Markoc chain also serves as a tool to deal with a countable-state Markov chain. The convergence property given in Section 5 can be used in many cases to construct a modified countable-state Markov chain such that the GTH algorithm can be performed in the approximation. This convergence property, together with the fact that the censored Markov chain provides an approximation with a minimal error under thel1-norm, leads to efficient stable computations using the GTH algorithm.

The rest of the paper is organized as follows: the GTH algorithm is introduced and discussed in Section 2; the censored Markov chain is reviewed in Section 3, in which we show that each elimination through using the GTH algorithm results in a censored Markov chain; the RG-factorization is presented in Section 4, which is a probabilistic counterpart to the LU-decomposition for Gaussian elimination; the RG-factorization can be considered as an extended version of the GTH algorithm for a system consisting of infinitely many linear equations.

2 GTH algorithm

The GTH algorithm is a numerical algorithm for computing the stationary distribution of a finite-state Markov chain. Mathematically, GTH algorithm is a rearrangement of Gaussian elimination. The GTH algorithm is numerically stable, since it starts with smallest entities and subtractions are avoided after the rearrangement, while Gaussian elimination can become numerically unstable if the number of states becomes large. The GTH algorithm also possesses a probabilistic interpretation in terms of the censoring process.

We start the GTH algorithm with introducing the Markov chain.

Definition 2.1(Markov chain) A discrete time stochastic process {Xn,n=0,1,2,…}, whereXntakes values on a finite or countable set, sayS={1,2,…}, referred to as the state space, is called a Markov chain if the following Markovian property holds:

P(Xn+1=j|Xn=i,Xn-1=in-1,…,X1=i1,X0=i0)=pi,j

for all statesi0,i1, …,in-1,i,jand alln≥0. The Markov chain is called a finite-state Markov chain ifSis finite.

We consider a finite-state Markov chain in this section with the state space

S={1,2,…,N}

and the probability transition matrix

For a finite-state Markov chain, it is well-known that ifP, or the Markov chain, is irreducible then there exists a unique stationary probability vector (distribution)

π=(π1,π2,…,πN)

satisfying

Writing out in detail, the equationπ=πPis equivalent to the followingNequations (referred to as steady-state, or equilibrium, or stationary equations):

(2.1)

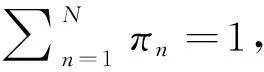
The focus of the GTH algorithm is to numerically compute the stationary probability vector. The basic GTH algorithm consists of two portions: forward eliminations and back substitutions.

It can be directly verified that

(2.2)

is a stochastic matrix, or a new Markov chain.

We then repeat the above elimination process to eliminateπN-1,πN-2, …,πnto have the following coefficients

andπjsatisfy the following equation:

(2.3)

The matrix of these coefficients:

(2.4)

defines a Markov chain.

π1=π1·1.

Backsubstitutions: To find the solution forπj, the GTH performs the back substitution. Define

r1=1,rj=πj/π1,j=2,3,…,N.

Since one of the two equations is redundant, we take the second one to have

Recall thatr=(r1,r2,…,rN) andπ=(π1,π2,…,πN) are different only by a constant, andπis a probability vector, we can easily normalizerto have

(2.5)

It is not difficult to see the mathematical equivalence between the GTH algorithm and Gaussian elimination. As indicated earlier, Gaussian elimination is usually numerically unstable whenNis large, say 10,000 or larger, while the GTH algorithm is very stable.

3 Censored Markov chains

The GTH algorithm has probabilistic interpretations. During the forward elimination, each step results in a new Markov chain with the state space one state fewer than the previous state space. In fact, each of these Markov chains is a so-called censored Markov chain, which will be discussed in this section.

The censored process is also referred to as a watched process since it is obtained by watchingXnonly when it is inE. It is also referred to as an embedded Markov chain since the time (or the state space) of the censored process is embedded in the time (or the state space) of the original process. The following lemma is a summary of some basic properties of the censored process.

(iii) IfE1andE2are two non-empty subsets of the state spaceSandE2is a subset ofE1, then

PE2=(PE1)E2.

The concept of the censored Markov chain was first introduced and studied by Lévy [16,17,18]. It was then used by Kemeny, Snell and Knapp [13] for proving the uniqueness of the invariant vector for a recurrent countable-state Markov chain. This embedded Markov chain was an approximation tool in the book by Freedman [3] for countable-state Markov chains. When the censored Markov chainis used to approximate the stationary distribution, Zhao and Liu [33] proved that it has the smallest error inl1-norm among all possible approximations.

Now, we discuss the connection between the GTH algorithm and the censored Markov chain. First, it is easy to check that if we letEn={1,2,…,n}, then the Markov chainPN-1in (2.2) is the censored Markov chainPEN-1, andPnin (2.4) is the censored Markov chainPEn-1according to Lemma 3.1. The expression for the stationary distribution given in (2.5) is an immediate consequence of Lemma 3.1-(ii). More probabilistic interpretations for the GTH algorithms can be provided:

4 RG-factorization

Mathematically, the GTH algorithm is equivalent to Gaussian elimination, which in turn is equivalent to an LU-factorization (or UL-factorization). In this section, we discussion the RG-factorization for Markov chains and show that the GTH algorithm is equivalent to the RG-factorization.

The RG-factorization discussed here is one of the versions of the so-called Wiener-Hopf-type factorization. This version of factorization is given in terms of the dual measures, the RG-measures, of the Markov chain. People who are interested in this topiccould refer to the literature references, including Heyman [9], Zhao, Li and Braun [31], Zhao [30], Li and Zhao [20,21,22].

Consider an irreducible countable-state Markov chain with its probability transition matrixPon the state spaceS={1,2,3,…}, given by

(4.1)

Define a pair of dual measures as follows: for 1≤i≤j, defineri,jto be the expected number of visits to statejbefore hitting any statej≥1, definegi,jto be the probability of hitting statejfor the first time, given that the process starts in statei.

One of the most important properties for the RG-measures is the invariance under censoring, which is stated in the following theorem.

(4.2)

and for given1≤j

(4.3)

The RG-factorization of the Markov chainPis given in the following theorem.

Theorem 4.2(RG-factorization, Theorem 13 in [30]) For the Markov chain defined by (4.1), we have

I-P=[I-RU][I-ΨD][I-GL],

(4.4)

where

ΨD=diag(ψ1,ψ2,…，ψN)

The RG-factorization of the GTH algorithm is an immediate consequence of the above theorem and the invariance of the RG-measures under censoring.

Corollary 4.1(RG-factorizationofGTHalgorithm)TheGTHalgorithmisequivalenttothefollowingRG-factorization:

I-P=[I-RU][I-ΨD][I-GL],

where

ΨD=diag(ψ1,ψ2,…,ψN),

and

Specifically,forn=1,2,…,N,

5 Extending GTH to countable-state Markov chains

Gaussian elimination is a method in linear algebra for solving a system of finitely many linear equations. Since linear algebra deals with linear spaces with a finite dimension, there is no Gaussian elimination version for a system consisting of infinitely many linear equations. The RG-factorization, together with the censored Markov chain, can be treated as an extended version of the GTH algorithm, since the UL-factorization formally allows us to perform forward eliminations and back substitutions to compute the stationary vectorπ. However, in order to practically start the elimination, we need a start state, not the infinite, which leads to various truncation methods.

An augmentation is a method using a non-negative matrixANsuch that

(5.1)

is stochastic. Popular augmentations include the censored Markov chain, the last column augmentation (add the missing probabilities to the last column), the first column augmentation (add the missing probability to the first column), and more generally (than the last and first column augmentations), the linear augmentation (add the missing probabilities linearly to the firstNcolumns).

This lemma says that if the sequenceEn(not necessarily equal to {1,2,…,n}) of subsets of the state space converges to the state spaceS, then the sequence of the censored Markov chains converges to the original chain.

Theorem 5.1(Theorem 7 in [30]) LetP=(pi,j)i,j=1,2,…be the transition matrix of a recurrent Markov chain on the positive integers. For an integerω>0, letP(ω)=(pi,j(ω))i,j=1,2,…be a matrix such that

pi,j(ω)=pi,j, fori,j≤ω

andP(ω) is either a stochastic or a substochastic matrix. For any fixedn≥0, letEn={1,2,…,n} be the censoring set. Then,

(5.2)

This theorem provides us with many options to construct an infinite stochastic matrixP(ω) with the same northwest cornerTωsuch that the censored Markov chainPEN(ω) can be easily obtained. Then, we can apply the GTH algorithm to the finite-state Markov chainPEN(ω) to compute the stationary probability vectorπNfor the censored Markov chainPEN(ω). According to the above theorem (Theorem 5.1),πNis an approximation toπ. This procedure also results in an approximation with an “approximate” minimal error in the sense ofl1-form based on the main result in Zhao [33]. We provide a brief discussion here.

It is worthwhile to comment here that not all augmentations are convergent. For example, the popular last column augmentation may not be convergent (see for example, [4]).

The following result guarantees a minimal error sum for the censored Markov chain.

Theorem 5.2(Best augmentation, [33]) The censored Markov chain is an augmentation method such that the error suml1(K,∞) is the minimum.

The first column augmentation is the worst under thel1-norm and the last column augmentation, if it is convergent, is the best under thel∞-norm (see also [9]). Other references on augmentations include [14,23,25,29], and references therein.

6 Concluding words

This review paper is dedicated to Dr. Winfried Grassmann, who is my Ph.D. supervisor, who directed me to the area of queueing theory and applied/computational probability. The GTH algorithm is one of his celebrated contributions to applied probability, and it is now a standard textbook content for computations of Markov chains.