李文智， 薛亚奎

(中北大学 理学院，山西 太原 030051)

1 引 言

纵观人类历史，传染病一直是危害人类生存与发展的巨大挑战.目前，人类对于传染病的预防以及治疗都有了很大的进步，但传染病的突发性是不可预测的，所以仍要保持高度警惕.对于某些传染病而言，易感者中会存在患病风险更高的职业，这类人群就是传染病的高危人群.如非典时期，一线的医护人员就是一类高危人群[1]；又如在布鲁氏菌病的传播中，兽医也是易受感染的高危险人群[2].

1927年Kermack和Mckendrick提出了用动力学方法来研究流行病的传播[3].此后，根据流行病的特点，建立不同的数学模型，再现疾病流行的规律，为疾病流行状况的预测和防治策略提出了理论依据[4-7].近年来，许多作者研究了常微分方程的流行病学模型，这些系统的重要研究主题是阈值的存在(该阈值可区分传染病是否会消亡)，无病平衡点和地方平衡点的局部和全局稳定性，周期解的存在，持久性和疾病的灭绝[8-11].由于易感者中存在某些特定职业的高危人群，因此通过将易感人群分类来建立数学模型，可以更好地分析某些传染病的流行规律.本文划分易感者中的高危人群和低危人群，且考虑患者存在接受医院治疗或通过体内抗体等因素自然抵抗疾病的情况，研究在饱和治疗率内的医院治疗对于疾病传播控制的影响.

2 模型的建立

通过对易感者分类为高危人群和低危人群，把疾病流行区域的人口总数N(t)分为五类：高危易感者S1(t)、低危易感者S2(t)、潜伏者E(t)、感染者I(t)和恢复者R(t)，所以

N(t)=S1(t)+S2(t)+E(t)+I(t)+R(t)

建立的传染病模型为

(1)

由于模型(1)的其他方程均不含有R,所以只需要以下的子系统

(2)

其中Λ表示人群的输入率；μ表示人类的自然死亡率；β1表示低危易感者与染病者接触的感染率；β2表示高危易感者与染病后死亡者接触的感染率；σ表示低危易感者转换为高危易感者的转化率；δ表示高危易感者转换为低危易感者的转化率；ε表示潜伏期的爆发率；γ表示染病者的自然恢复率；α表示感染者的因病死亡率；k为治愈率，一般k>0.

3 基本再生数和平衡点存在性

(3)

εE*-αI*-μI*-γI*-kI*=0

整理求得

P(I*)=AI*2+BI*+C=0

其中

则可得下列关于平衡点的存在性的结果：

1)若R0>1(此时C<0)，则模型存在唯一的地方病平衡点；

2)若R0>1,且B<0,则模型存在两个地方病平衡点；

3)若B<0,且R0=1时，模型存在唯一的地方病平衡点.

4 平衡点的稳定性

定理4.1 如果R0<1,模型(2)的无病平衡点P0在Γ内是全局渐近稳定的；如果R0>1,无病平衡点P0是不稳定的.

证明：模型(2)在无病平衡点P0处的线性化系统的Jacobian矩阵为：

对应的特征方程为：

其他根的特征方程简记为

其中

由此可得，当R0<1时，λ3和λ4都为负，系统(2)在无病平衡点P0处是局部渐近稳定的；当R0>1时，解存在正根，系统(2)的无病平衡点不稳定.

构造Lyapunov函数：

对V关于模型(2)求导：

系统(2)在无病平衡点处可知

定理4.2 如果R0>1,系统(2)的地方病平衡点P*在Γ内是全局渐近稳定的.

证明：模型(2)在地方病平衡点P*=(S*,E*,I*,D*)处的线性化系统的Jacobian矩阵为：

特征方程简记为λ4+a1λ3+a2λ2+a3λ+a4=0,地方病平衡点P*是局部渐近稳定的，当且仅当特征方程的所有特征根具有负实部，根据Routh-Hurwitz判据，若Hk>0,特征方程的所有特征根均具有负实部.

其中

a1=(β1I*+σ+μ)+(β2I*+δ+μ)+(ε+μ)+(α+μ+γ+k)

a2=(α+μ+γ+k)(ε+μ)+(α+μ+γ+k)(β1I*+σ+μ)+(α+μ+γ+k)(β2I*+δ+μ)+

(ε+μ)(β1I*+σ+μ)+(ε+μ)(β2I*+δ+μ)+(β1I*+σ+μ)(β2I*+δ+μ)-δσ-

a3=(β1I*+σ+μ)(ε+μ)(α+μ+γ+k)+(α+μ+γ+k)(β2I*+δ+μ)(ε+μ)+

(α+μ+γ)(β1I*+σ+μ)(β2I*+δ+μ)+(ε+μ)(β1I*+σ+μ)(β2I*+δ+μ)-

με(β1S1*+β2S2*)-εβ1S1*(β2I*+δ+μ)-εβ2S2*(β1I*+σ+μ)-

(α+μ+γ+k)δσ-(ε+μ)δσ

a4=(α+μ+γ+k)(β1I*+σ+μ)(ε+μ)(β2I*+δ+μ)-δσ(α+μ+γ+k)(ε+μ)-

通过计算可知

因此R0>1时，系统的地方病平衡点P*是局部渐近稳定的.

构造Lyapunov函数：

当f(z)=z-1-lnz,z∈R+,当且仅当z=1时f(z)=0

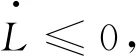
对L关于模型(2)求导得：

则通过替换可求得：

5 数值模拟和讨论

运用软件MATLAB进行数值模拟，考虑不同的医院治愈率在平衡点处的稳定性，且医院治愈率在饱和治愈率内，则有以下情形.

(a)k=0.3 (b)k=0.6

图1 参数k对无病平衡点处稳定性的影响

Fig.1 The effect of parameterkon the stability of disease-free equilibrium point

图1中，(a)为取参数Λ=10,σ=0.01,α=0.25,γ=0.05,β1=0.005,β2=0.015,μ=0.05,ε=0.02，k=0.3,δ=0.005,无病平衡点P0在可行域内是全局渐近稳定的.通过改变医疗治愈率(饱和治愈率内)， 研究其对稳定性的影响.(b)为改变医疗治愈率，k=0.6,无病平衡点P0在可行域内是全局渐近稳定的，R0随着医疗治愈率的增加而减小，疾病趋于消亡的时间也相应地缩短.

(a)k=0.3 (b)k=0.6

图2 参数k对地方病平衡点处稳定性的影响

Fig.2 The effect of parameterkon the stability of endemic equilibrium point

图2中，(a)为取参数Λ=50,σ=0.01,α=0.25,γ=0.05,β1=0.005,β2=0.015,μ=0.05,ε=0.02，k=0.3,δ=0.005,地方病平衡点P*是全局渐近稳定的.同样通过改变医疗治愈率影响因子，来探讨其对传染病的影响效果.(b)为改变医疗治愈率，k=0.6,地方病平衡点P0在可行域内是全局渐近稳定的，R0随着医疗治愈率的增加而减小，疾病趋于稳定的时间也相应缩短.

6 结 语

建立了易感者分为高危人群和低危人群的模型，分析其平衡点的存在性和稳定性，通过第二代生成矩阵的方法得到了疾病能否流行的阈值R0,通过构造Lyapunov函数，并运用Lassalle不变性原理，得到以下的两个结论：其一是发现病毒能否得到有效控制主要由基本再生数R0决定，而提高医疗治愈率是控制病毒爆发的有效途径，从模型的计算中可以得到如果R0<1,无病平衡点P0是全局渐近稳定的；如果R0>1,地方病平衡点P*是全局渐近稳定的，并通过数值模拟，验证了模型的稳定性；其二是提高医院的医疗设备率，增大对医疗机构的投资，对床位以及资源设施的完善，并且通过政府的宣传，加大高危工作人员的防护措施，减少发病率，从而减少大规模的感染发生.因此，研究具有不同易感人群的传染病模型对于预测和控制传染病的流行都有重要的理论价值和实际意义.