■蒋庆富

已知两个非零向量a，b，那么|a||b|·cosθ(θ是a与b的夹角)叫作向量a与b的数量积或内积，记作a·b。若向量a=(x1，y1)，b=(x2，y2)，则a·b=x1x2+y1y2。

一、求向量的数量积

例1 设△A B C的外接圆的圆心为P，半径为3，若( )。

解：由的外接圆的圆心为P，半径为3，可知两向量的。由向量加法的平行四边形法则可和向量的模是3。易得知 ，的夹角为120°，所以应选A。

评析：正确理解的意义是解答本题的关键。

例2 如图1所示，正六边形A B C D E F的边长为1，则

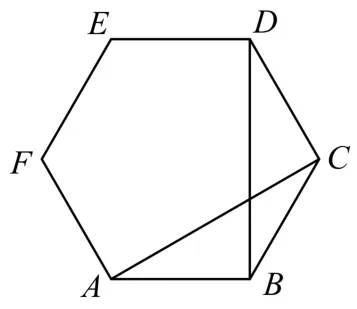
图1

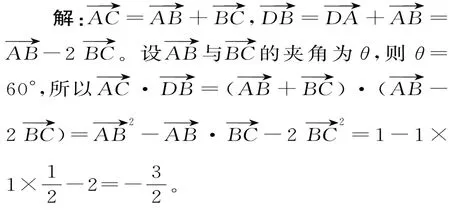
评析：解题时要注意向量与的夹角是60°，而不是120°。

二、求向量的模

例3 如图2所示，在△A B C中，O为B C的中点，若A B=1，A C=3，与的夹角为60°，则

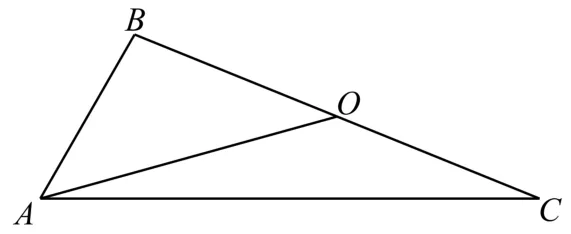
图2

评析：利用向量之间的关系构造是解答本题的关键。

三、判断三角形的形状

例4 若O为△A B C所在平面内任一点，且满足=0，则△A B C的形状为( )。

表3方案侧重于对现有各类设备的数量而不是可用生产时间进行拆分和最优分配，相较于表1和表2方案，避免了生产流程的频繁切换，大大简化了对设备的管理和调度．

A.等腰三角形

B.直角三角形

C.正三角形

D.等腰直角三角形

解：由，可得

评析：两个向量相减时，其差向量的方向是指向被减向量的终点。

四、求面积问题

例5 在四边形A B C D中则该四边形的面积为( )。

解：因为，所以对角线A C，B D互相垂直，所以该四边形的面积S=应选C。

评析：由得到对角线A C，B D互相垂直是解题的关键。

例6 已知，且，则以为邻边的平行四边形的面积为( )。

解：因为，所以，所以所求的平行四边形的面积为应选A。

评析：由题设条件求出是解答本题的关键。

五、求向量的夹角

例7 已知向量a·(a+2b)=0，|a|=2，|b|=2，则向量a与b的夹角为( )。

解：设θ是a与b的夹角。由a·(a+2b)=0，可得|a|2+2a·b=0。根据向量数量积的定义及已知条件可得22+2×2×2×cosθ=0，所以。又因为θ∈[0，π]，所以应选B。

评析：利用可求两向量的夹角，但要注意夹角θ∈[0，π]。

六、求参数的值

例8 已知菱形A B C D的边长为6，∠A B D=30°，点E，F分别在边B C，D C上，B C=2B E，C D=λ C F。若则λ的值为( )。

A.2 B.3

C.4 D.5

评析：把向量用基底向量和表示是解题的关键，但要注意作为基底的两个向量必须是不共线的。

七、求取值范围问题

例9 已知向量a，b，c共面，a，b，c均为单位向量，且a·b=0，则|a+b-c|的取值范围是( )。

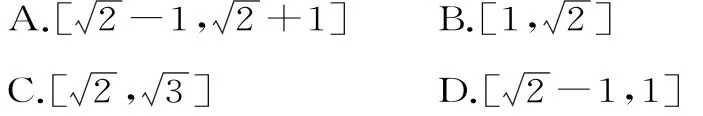
解：设向量=α，=β。

因为a·b=0，所以a⊥b，则或α，于是可得|a+b-c|2=a2+b2+c2+2a·b-2a·c-2b·c=3-2 cosα

评析：求解本题要注意两点：一是角α与β之间的关系；二是正确运用两角和的余弦公式求最值。