高考“概率与统计”题:九个靶点,一举突破
2020-04-28安徽省利辛高级中学
■安徽省利辛高级中学
考试范围与要求:1.理解取有限个值的离散型随机变量及其分布列的概念,认识分布列刻画随机现象的重要性,会求某些取有限个值的离散型随机变量的分布列。2.了解超几何分布,并能进行简单应用。3.了解条件概率的概念,了解两个事件互相独立的概念,理解n次独立重复试验模型及二项分布,并能解决一些简单问题。4.理解取有限个值的离散型随机变量的均值、方差的概念,会求简单离散型随机变量的均值、方差,并能利用离散型随机变量的均值、方差概念解决一些简单问题。5.借助直观直方图认识正态分布曲线的特点及曲线所表示的意义。6.了解回归分析的思想、方法及其简单应用。7.了解独立性检验的思想、方法及其初步应用。
要点简析:以知识点1,2,3,5 为背景的试题以选择题或填空题为主。以知识点4为背景的试题常以解答题的形式出现,试题背景来源于社会实际,贴近生活,易于理解,体现了概率与统计知识与社会生活的密切联系,展现了概率与统计学的魅力,渗透了数学建模等核心素养。以知识点6,7为背景的统计试题,三种题型均有可能出现,对回归分析和独立性检验的考查以解答题为主,命题素材新颖,特别关注应用与创新,突显新课改精神。下面对本模块的高考核心靶点进行例析与归纳。
高考靶点一 条件概率及其应用
例1(2016 年全国Ⅱ卷)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如表1:

表1
设该险种一续保人一年内出险次数与相应概率如表2:

表2
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值。
解析:(1)设A表示事件“一续保人本年度的保费高于基本保费”,则事件A发生时一年内出险次数大于1,故P(A)=0.20+0.20+0.10+0.05=0.55。
(2)设B表示事件“一续保人本年度的保费比基本保费高出60%”,则事件B发生当且仅当一年内出险次数大于3,故P(B)=0.10+0.05=0.15。又P(AB)=P(B),故P(B|A)=。
(3)记续保人本年度的保费为X,则X的分布列如表3:

表3
E(X)=0.85a×0.30+a×0.15+1.25a×0.20+1.5a×0.20+1.75a×0.10+2a×0.05=1.23a。因此,续保人本年度的平均保费与基本保费的比值为1.23。
方法突破:1.设A、B是两个事件,且P(A)>0,称P(B|A)=为在事件A发生条件下事件B发生的概率,其中P(B|A)=既是条件概率的定义,也是条件概率的公式。
2.条件概率的性质:①0≤P(B|A)≤1;②如果B和C是两个互斥事件,那么P(B∪C|A)=P(B|A)+P(C|A);③若A、B相互独立,则P(B|A)=P(B)。
3.条件概率的两种求解方法:(1)定义法,先求P(A)和P(AB),再由P(B|A)=求之;(2)基本事件法,借助古典概型概率公式,先求事件A包含的基本事件数n(A),再求事件AB所包含的基本事件数n(AB),得P(B|A)=。
高考靶点二 相互独立事件的概率及其应用
例2(2019 年沈阳市高三检测)某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种。方案一:每满200元减50元;方案二:每满200元可抽奖一次,具体规则是依次从装有3 个红球、1 个白球的甲箱,装有2 个红球、2 个白球的乙箱,以及装有1个红球、3 个白球的丙箱中各随机摸出1个球(注:所有小球仅颜色有区别),所得结果和享受的优惠如表4:

表4
(1)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(2)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算。
解析:(1)设事件A为“顾客获得半价优惠”,则P(A)=,所以两个顾客各抽奖一次,至少一个人获得半价优惠的概率P=。
(2)若该顾客选择方案一,则付款金额为320-50=270(元)。若该顾客选择方案二,记付款金额为X元,则X可取得值为160,224,256,320,P(X=160)=,P(X=224)==,P(X=256)=,P(X=320)=。
所以E(X)==240(元)。
因为270>240,所以方案二更划算。
方法突破:求相互独立事件同时发生的概率的方法:(1)利用互相独立事件的概率乘法公式直接求解;(2)正面计算较烦琐或难以入手时,可从其对立事件入手,如本例第一问,由题意结合对立事件的概率公式求解。本题以商场举行优惠促销活动为背景考查了离散型随机变量的数学期望的应用。
高考靶点三 独立重复与二项分布
例3(2020 届河北衡水第一次调研)生蚝即牡蛎,亚热带、热带沿海都适宜蚝的养殖,蚝乃软体有壳、依附寄生的动物,咸淡水交界所产尤为肥美,因此,生蚝成为了一年四季不可或缺的美食。某饭店从某水产养殖场大量购进了一批生蚝,并随机抽取了40只统计质量,得到的结果如图1所示。(用区间中点值代表该组数据的平均值)
(1)若购进这批生蚝500 kg,试估计这批生蚝的数量;(结果四舍五入,保留整数)
(2)以频率估计概率,若在本次购买的生蚝中随机挑选4 只,记质量在[5,25)内的生蚝的只数为X,求X的分布列及数学期望。
解析:①先估算出生蚝的平均质量为28.5g,由此能估计出这批生蚝的数量。②任意挑选一只,质量在[5,25)内的概率p=,X的可能取值为0,1,2,3,4,X~,分别求出相应的概率,由此能求出X的分布列和数学期望。
(1)由图1 中的数据可以估算生蚝的平均质量为:
(2)由图1 中数据知,任意挑选一只,质量在[5,25)内的概率为,则由题意可知X~。X的可能取值为0,1,2,3,4,则P(X=0)=;
所以X的分布列如表5:
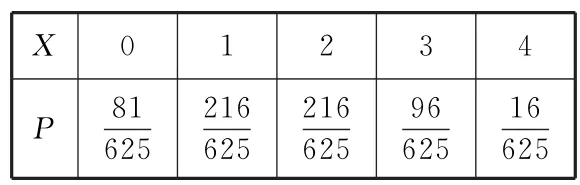
表5
由X~,得E(X)=。
方法突破:解决二项分布问题的关键:(1)二项分布的判断,判断一个随机变量是否服从二项分布,应判断两个方面,一是判断是否为n次独立重复试验,二是判断随机变量是否为这n次独立重复试验中某事件发生的次数。(2)二项分布的期望与方差公式:若X~B(n,p),则P(X=k)=(1-p)n-k(k=0,1,2,…,n),E(X)=np,D(X)=np(1-p)。(3)特别地,若n=1,又称随机变量X服从两点分布,则E(X)=p,D(X)=p(1-p)。
高考靶点四 超几何分布
例4(2020年湖北省部分重点中学高三联考)为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅一户),如表6:

表6
某市随机抽取10个用户同一个月的用电情况,如表7所示:

表7
(1)若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算居民用电户月用电410度时应交电费多少元。
(2)现要在这10 户家庭中任意选取3户,求取到第二阶梯电量的用户数的分布列与期望。
(3)以表中抽到的10个用户作为样本估计全市居民用电,现从全市中依次抽取10户,若抽到k户月用电量为第一阶梯的可能性最大,求k的值。
解析:(1)由题意知,居民用电户月用电410度时应交电费210×0.5+(400-210)×0.6+(410-400)×0.8=227(元)。
(2)设取到第二阶梯电量的用户数为ξ,可知第二阶梯电量的用户有3 户,则ξ可取0,1,2,3,P(ξ=0)=,P(ξ=1)=,P(ξ=2)=,P(ξ=3)=。
故ξ的分布列如表8:
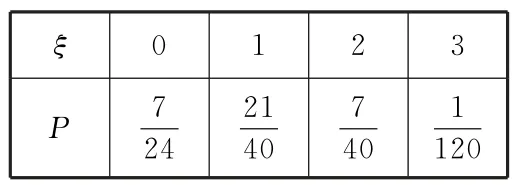
表8
所以E(ξ)=。
(3)由题意可知,从全市中抽取10户,设其中月用电量为第一阶梯的户数为X,则X~(k=0,1,2,3,…,10)。
方法突破:解决超几何分布的实际应用问题时,应关注:(1)定义:在含有M件次品的N件产品中,任取n件,其中恰有X件次品数,则事件{X=k}发生的概率为P(X=k)=,k=0,1,2,…,m,其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*称分布列为超几何分布列。如果随机变量X的分布列为超几何分布列,则称随机变量X服从超几何分布。(2)其特点:①对于服从该分布的随机变量,其分布列可直接应用公式给出,如E(X)=,D(X)=,可作参考备之。②该分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数,随机变量取值的概率实质上是古典概型。
高考靶点五 正态分布
例5(洛阳市2020学年上学期高三尖子生联考)“过大年,吃水饺”是我国不少地方过春节的一大习俗。2019年春节前夕,A市某质量检测部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标值,所得频率分布直方图如图2。
(1)求所抽取的100 包速冻水饺该项质量指标值的样本平均数(同一组中的数据用该组区间的中点值作代表)。
(2)(i)由频率分布直方图可以认为,速冻水饺的该项质量指标值Z服从正态分布N(μ,σ2),利用该正态分布,求Z落在(14.55,38.45]内的概率;(ii)将频率视为概率,若某人从该市某超市购买了4 包这种品牌的速冻水饺,记这4 包速冻水饺中该项质量指标值位于(10,30]内的包数为X,求X的分布列和数学期望。
附:计算得所抽查的这100 包速冻水饺的该项质量指标值的标准差σ=≈11.95,若ξ~N(μ,σ2),则P(μ-σ<ξ≤μ+σ)≈0.682 6,P(μ-2σ<ξ≤μ+2σ)≈0.954 4。
解析:(1)所抽取的100包速冻水饺该项质量指标值的平均数为:
(2)(i)因为Z服从正态分布N(μ,σ2),且μ=26.5,σ≈11.95,所以P(14.55<Z≤38.45)=P(26.5-11.95<Z≤26.5+11.95)≈0.682 6,Z落在(14.55,38.45]内的概率是0.682 6。
(ii)根据题意得X~,P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=,P(X=4)=。
故X的分布列如表9:

表9
则E(X)==2。
方法突破:解此类问题的关键是利用正态曲线的对称性,把待求区间内的概率向已知区间内的概率转化,解题时要充分结合图形进行分析、求解,要注意数形结合思想及化归思想的运用。(1)熟记P(μ-σ<X≤μ+σ),P(μ-2σ<X≤μ+2σ),P(μ-3σ<X≤μ+3σ)的值。(2)充分利用正态曲线的对称性和曲线与x轴之间面积为1。(3)正态曲线关于直线x=μ对称,从而在关于x=μ对称的区间上概率相同。(4)P(X≤a)=1-P(X≥a),P(X≤μ-a)=P(X≥μ+a)。
高考靶点六 变量的相关性与回归分析
例6(昆明市2019届高考模拟考试)改革开放以来,我国农村7 亿多贫困人口摆脱贫困,贫困发生率由1978年的97.5%下降到2018年底的1.4%,创造了人类减贫史上的中国奇迹,为全球减贫事业贡献了中国智慧和中国方案。“贫困发生率”是指低于贫困线的人口占全体人口的比例。2012 年至2018年我国贫困发生率的数据如表10:

表10
(1)从表中所给的7 个贫困发生率数据中任选2个,求至少有1个低于5%的概率;
(2)设年份代码x=t-2 015,利用回归方程,分析2012 年至2018 年贫困发生率的变化情况,并预测2019年贫困发生率。
解析:(1)所求概率P=。
(2)由题意可得表11:

表11
方法突破:(1)本模块已成为高考命题的热点之一,要求理解用回归分析处理相关关系的数学方法,理解最小二乘法,了解回归的基本思想方法及其简单应用,充分表明新课程对统计思想的重视。(2)求回归性方程时,关键是正确求其系数,由于计算量大,计算时需谨慎;数据分析后,关键是如何获得与解释结论;同时,应用过程就是正确构造数学模型,即数学建模。因此要不断地提升同学们的数学核心素养。
高考靶点七 独立性检验的基本思想、方法及其简单应用
例7(大同市2020届高三调研卷)某学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计,其中对教师教学水平给出好评的学生人数为总数的60%,对教师管理水平给出好评的学生人数为总数的75%,对教师教学水平和教师管理水平都给出好评的有120人。
(1)填写下面对教师教学水平和教师管理水平评价的2×2列联表(表12):
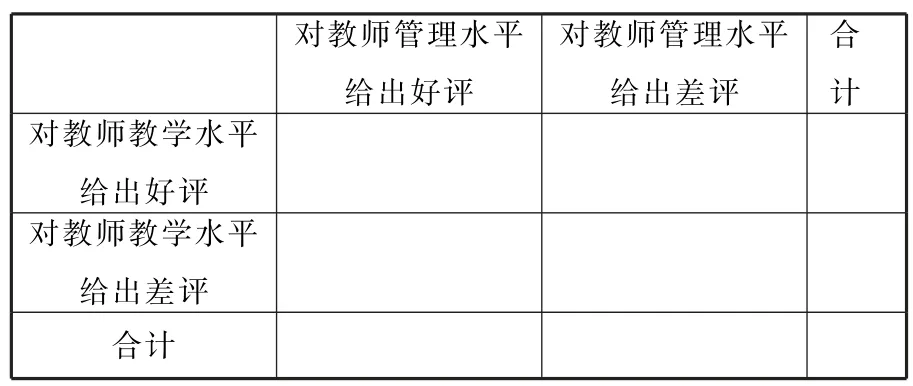
表12
问:是否可以在犯错误的概率不超过0.1%的前提下,认为对教师教学水平给出好评与对教师管理水平给出好评有关?
(2)若将频率视为概率,有4名教师参与了此次评价,设教师教学水平和教师管理水平全为好评的教师人数为随机变量X。
①求教师教学水平和教师管理水平全为好评的教师人数X的分布列(概率用数值作答);
②求X的数学期望和方差。
附:K2=,其中n=a+b+c+d。

表13
解析:(1)由题意可得对教师教学水平和教师管理水平评价的2×2列联表:
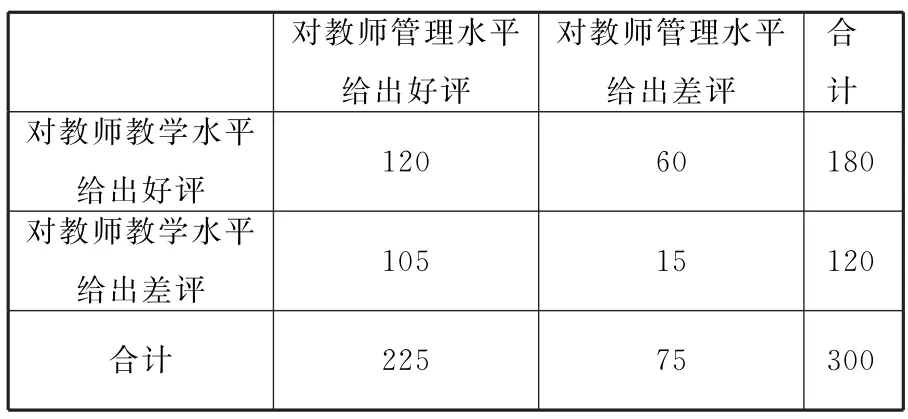
表14
K2=≈16.667>10.828。
故可以在犯错误的概率不超过0.1%的前提下,认为对教师教学水平给出好评与对教师管理水平给出好评有关。
故X的分布列如表15:
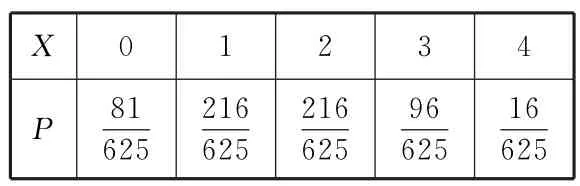
表15
②由于X~,则E(X)=4×=,D(X)=。
方法突破:运用独立性检验的思想考查两个分类变量是否有关系是高考命题的热点,其求解关键步骤为:根据样本数据制成2×2列联表;根据公式计算出k的值;比较k的值与临界值的大小关系,作出统计推断,确定给出这种判断的可靠程度。
高考靶点八 概率、统计与其他知识的综合问题
例8(武汉市2020届高三质量检测)武汉又称江城,是湖北省省会城市,被誉为中部地区中心城市,它不仅有着深厚的历史积淀与丰富的民俗文化,更有着众多旅游景点,每年来武汉参观旅游的人数不胜数,其中黄鹤楼与东湖被称为两张名片。为合理配置旅游资源,现对已游览黄鹤楼景点的游客进行随机问卷调查,若不游玩东湖记1分,若继续游玩东湖记2 分,每位游客选择是否游览东湖景点的概率均为,游客之间选择意愿相互独立。
(1)从游客中随机抽取3人,记总得分为随机变量X,求X的分布列与数学期望。
(2)(i)若从游客中随机抽取m人,记总得分恰为m的概率为Am,求数列{Am}的前10项和;
(ii)在对所有游客进行随机问卷调查过程中,记已调查过的累计得分恰为n的概率为Bn,探讨Bn与Bn-1之间的关系,并求数列{Bn}的通项公式。
解析:(1)X的可能取值为3,4,5,6,P(X=3)=,P(x=4)=,P(X=5)=,P(X=6)=。
故X的分布列如表16:

表16
(2)(i)总得分恰为m的概率Am=,数列{Am}是首项为,公比为的等比数列,前10 项和S10==。
(ii)已调查过的累计得分恰为n的概率为Bn,得不到n分的情况只有先得(n-1)分,再得2分,概率为,故1-,即Bn=。
故Bn=。
方法突破:解决此类综合题的关键是:(1)认真审题,合理、准确地建立概率、统计模型,判断随机变量的所有可能取值,根据概率分布类型,计算各随机变量取值时的概率、列出分布列;(2)根据知识间的综合类型找出知识交汇处的突破点,从而把模块间的综合转化为模块知识内的综合,然后在某知识体系内进行求解。
高考靶点九 利用概率与统计知识解释方案的合理性
例9(惠州市2020 届高三第一次调研)某种大型医疗检查机器生产商,对一次性购买2 台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:
方案一:交纳延保金7 000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2 000元;
方案二:交纳延保金10 000 元,在延保的两年内可免费维修4次,超过4次每次收取维修费1 000元。
某医院准备一次性购买2 台这种机器,现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50 台这种机器超过质保期后延保两年内维修的次数,如表17:
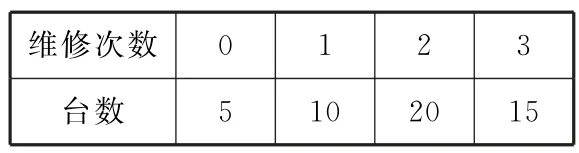
表17
以这50台机器维修次数的频率代替一台机器维修次数发生的概率,记X表示这两台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金与维修费用的和的期望值为决策依据,医院选择哪种延保方案更合算?
解析:(1)X所有可能的取值为0,1,2,3,4,5,6。
故X的分布列如表18:

表18
(2)选择延保方案一,所需延保金与维修费用的和Y1(单位:元)的分布列如表19:

表19
选择延保方案二,所需延保金与维修费用的和Y2(单位:元)的分布列如表20:
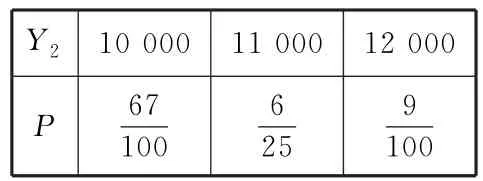
表20
因为E(Y1)>E(Y2),所以该医院选择延保方案二更合算。
方法突破:解决此类问题的关键是:以实际生产、生活等问题中的环保、民生、科技、旅游或经济效益或方案的合理性(优化问题)等为背景,准确建立概率、函数、数列等数学模型,然后根据整合的数据,并利用不同的特征值对研究对象给出定量计算或合理定性判断。
