王 治，万育基，余志先

（1.上海理工大学 理学院，上海 200093；2.上海师范大学 数理学院，上海 200234）

1 问题的提出

虽然状态依赖时滞的微分方程（SD-DDE）可以追溯到19 世纪，但该类型方程研究由于在各种情况下的频繁运用而再一次成为研究热点，见文献[1-4]。

Lv 等[3]研究了一种状态依赖时滞的扩散阶段结构模型，并得到了大波速下的行波解的存在性。Lin 等[4]进一步研究了状态依赖时滞的反应扩散方程：

的行波解的存在性，其中u(x,t)代表时刻t在x处的种群密度。

行波解的概念在1937 年由Kolmogorov 等[5]提出，用来解释动物基因的传播过程。行波解现象不仅存在于种群模型中，也存在于物理、化学、生物及神经网络等领域，见文献[3-5]。行波解也可以用来解释自然界中传播和震动现象，因而具有重要的实际意义。

尽管方程（1）中Laplacian 扩散模型应用广泛，但它表示的生态系统的一个重要缺点是这种扩散是一个局部扩散，这表明种群中的个体只能影响到局部范围。克服这类问题的常用方法是用卷积算子或积分微分方程来研究扩散系统，见文献[6-7]。Wan 等[8]研究状态依赖时滞的非局部的种群模型

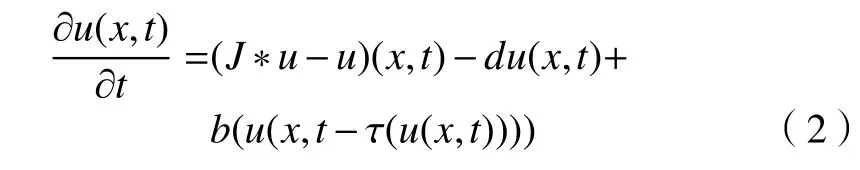
的行波解的存在性，其中u(x,t)代表在时刻t位置x处的种群密度，J*u-u是 一个非局部扩散算子，定义为若J(x-y)是从y位置跳跃到x位置的概率分布，则J*u代表个体从所有其他位置到x位置的种群数量，并且u(x,t)=代表从x位置处到其他位置的种群数量。在种群模型中，d为死亡率，b(u)为出生函数，τ(u)为种群密度依赖的成熟时滞。

本文考虑更一般的非局部带状态依赖时滞反应的扩散系统的行波解的存在性，方程如下

方程（3）的行波解，是一种定义在全空间上特殊的整体解，且具有如下形式：u(x,t)=φ(ξ),ξ=x+ct，

其中c＞0为波速，φ∈C1(R,R)为波像函数并满足方程

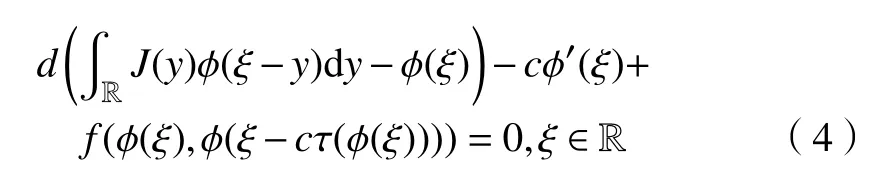
和渐近边界条件

特别地，称满足条件（5）的单调行波解为波前解。

2 主要结果

现在给出一些假设：

定理1假设a～e 成立，存在一个正常数c*，当c≥c*时，方程（4）存在一个非减的正的行波解u(t,x)=φ(x+ct)，且φ(-∞)=0,φ(+∞)=K。此外，

其中，λ1＞0为下列方程的最小实根。

3 主要结果的证明

问题（3）行波解的存在性的证明，将分成3 个部分来完成。首先，利用合适的上下解及有关假设构造一个算子所在集合 Γ；其次，证明定义的算子F:Γ→Γ在Bλ中关于范数‖·‖Bλ全连续；最后，利用Schauder 不动点定理，得到存在性定理。

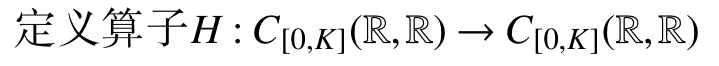
其中，β ＞d，C[0,K](R,R)={φ∈C(R,R)|0 ≤φ(ξ)≤K,ξ∈R}。进一步定义算子F:C[0,K](R,R)→C[0,K](R,R)

显然，算子F的一个不动点 φ就是方程（4）的解，即

因此，为了研究方程（4）解的存在性，只需研究算子F的不动点的存在性。

因为∂2f(u,v)≥0,(u,v)∈[0,K]2，容易知道函数f满足如下拟单调条件。

引理1假设a～c 成立，存在一个正常数β ＞使得

其 中，φ1,φ2∈C[0,K](R,R)，且 当ξ∈R,0 ≤φ2(ξ)≤φ1(ξ)≤K。

引理2假设a～d 成立，如果φ∈C[0,K](R,R)，对于任何c＞0，则有

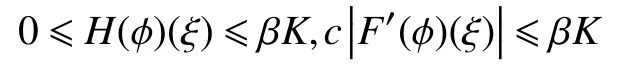
证明易证0 ≤H(φ)(ξ)≤βK。由算子F的定义，有

故得证。

现在，引入积分方程（9）的上下解的概念。

定义1一个连续有界的函数φ:R→[0,K]称为方程（9）的一个上解当且仅当满足如下条件：

方程（9）的一个下解也可以类似定义得到，只需将式（10）不等号反向。

当λ≥0,c≥0，定义一个函数Δ(c,λ)如下：

引理3假设a～d 成立，则存在唯一的c*＞0满足如下条件：

①若c≥c*，则存在两个正数0 ＜λ1≤λ2，Δ(c,λ1)=Δ(c,λ2)=0；

②若c＜c*，则对所有λ ＞0，Δ(c,λ)＜0；

③若c=c*，则 λ1=λ2=λ*，当c＞c*，则 λ1＜λ*＜λ2，

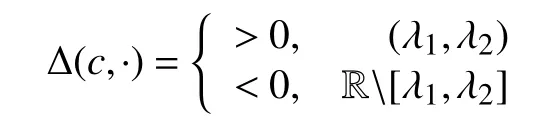
对于在引理3 中给定的常数c＞c*和λ1,λ2，定义连续函数[9-11]：

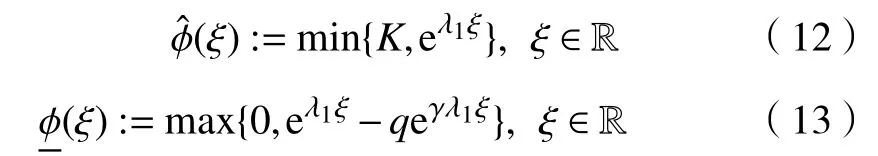
引理4假设a～d 成立，则对波速c＞c*，此时，存在一个β1＞0，当β ≥β1，ξ1,ξ2∈R时，

证明注意到

令β1=L1，即完成证明。

引理5假设a～d 成立，当波速c＞c*，与分别为方程（9）的一个上解和下解。

证明因为对ξ∈R，0 ≤φˆ(ξ)≤K，由引理1 知

且有

则

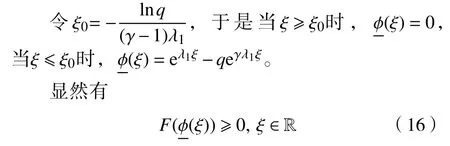
由假设条件e，存在δ1,δ2＞0,0 ＜L＜∞，当(u,v)∈[0,κ]2，使得

易知存在一个Q1(γ)≫1，当q≥Q1(γ)，有eλ1ξ-qeγλ1ξ≤κ。因此，0 ≤φ(ξ)≤κ。因为ξ0＜0，1+σi＞γ,i=1,2，故可得

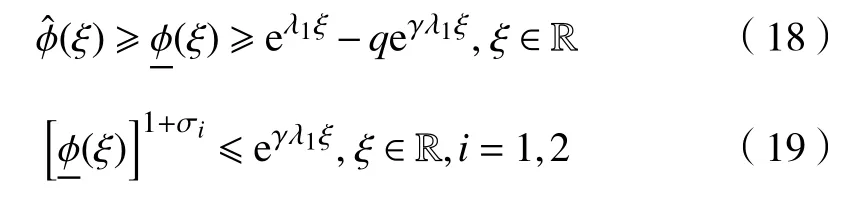
根据式（18）和式（19），可得

由式（20）得

结合式（16）和式（21），有

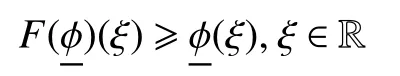
下面，将要通过Schauder 不定点定理来寻求算子F的不动点。为此，可以引进指数衰减范数。当0 ≤λ ≤λ1，定义

容易验证Bλ(R,R)是一个附有范数的一个Banach 空间。

易证集合Γ为非空、有界、闭凸集。对于在式（8）中定义的算子F，有如下引理成立。

引理6假设a～e 成立，

①F(Γ)⊂Γ;

②F:Γ→Γ在Bλ中关于范数‖·‖Bλ是全连续。

证明根据引理1～5，对任意φ∈Γ，有

且F(φ)(ξ)关于φ(ξ)∈C[0,K](R,R)是非减的，c|F′(φ)(ξ)|≤βK。因此，F(Γ)⊂Γ。

因f∈C1([0,K]2,R)，存在M＞0，满足|f(u1,v1)-f(u2,v2)|≤M(|u1-u2|+|v1-v2|)，其 中ui,vi∈[0,K],i=1,2。于是，对φ,ψ∈Γ，有

因此，可得

它表明F:Γ→Γ在Bλ(R,R)中关于范数‖·‖Bλ是连续的。另一方面，对任意φ∈Γ，ξ∈R，当ξ1≥ξ2，ξ1,ξ2∈R时，

这表明对于ξ∈R，{F(φ)(ξ):φ∈Γ}是一致有界并且等度连续。因此，通过Arzela-Ascoli 定理，对于在F(Γ)中任意给定的序列{ψn}n∈N，存在nk→∞和 ψ∈C(R,R)，使得在 R任何紧支集上(ξ)=ψ(ξ)关于 ξ一致成立。因为，对任意的，于是有即ψ(ξ)∈Γ。另外有

因此，对任意ε ＞0，可以找到M0＞0，使得对任意的|ξ|≥M0，可得

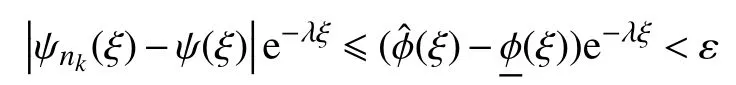
此外，当|ξ|≤M0时，一致存在，于是存在k*＞0，当k≥k*时，对任意的|ξ|≤M0，可得

由此可得，当k→∞时，所以，F:Γ→Γ在Bλ中关于范数‖·‖Bλ全连续。

定理1 的证明。

证明根据引理6 和Schauder 不动点定理，F存在一个不动点φ∈Γ。因φ(ξ)非减且有界，所以。由洛必达法则，可得

定理1 得证。