杨芸丞，孙雪丽，钟兆根

（海军航空大学，山东 烟台 264001）

0 引言

现代信息化战争中，跳频通信由于其低截获概率、组网方式灵活、信道衰减缓慢等优点，在军事通信、指挥、控制和情报系统中均得到了广泛应用［1］。对于信号侦察方而言，如何获取敌方跳频信号的参数信息，完成对跳频信号特征参数的准确估计具有重大的研究意义［2］。

传统的跳频信号参数估计算法，多以高斯白噪声为背景噪声模型。文献［3］利用短时傅里叶变换（Short-Time Fourier Transform，STFT），计算量小，但存在时间分辨率和频率分辨率矛盾的问题；文献［4］应用小波变换的方法对跳频信号进行分析，有效解决了时频分辨率矛盾的问题，但小波基难以选取，且算法计算量较大；文献［5］通过建立ARMA 模型估计跳变时刻和跳频频率，仅适用于正定条件；文献［6］对信号样本进行原子分解，将时频原子的参数值进行聚类，但也受限于计算复杂度过大；这些算法均可实现跳频参数的准确估计。但是，在实际的空间环境中，往往存在显著的非高斯性脉冲干扰，如电磁噪声、大气雷噪声等。研究表明，这类噪声近似于α 稳定分布模型。在该噪声影响下，以高斯白噪声为噪声模型的跳频参数估计方法性能显著下降乃至失效。鉴于此，文献［7］提出了分数低阶的平滑伪Wigner-Ville（SPWVD）的方法，有效抑制了脉冲噪声，但算法计算量大，不能达到瞬时估计的效果；文献［8］提出了一种分数低阶STFT 的方法，解决了计算量大的问题，但该方法受限于不确定性原理，不能同时得到较好的时间分辨率和频率分辨率。

针对α 稳定分布噪声背景下跳频参数盲估计问题，同时克服文献［8］的不足，本文首先对跳频信号进行两次窗函数长短不同的分数低阶STFT，得到两组时频数据，然后将两组时频数据点乘，得到新的时频表示，最后基于时频分析的跳频参数估计方法，实现跳频参数的估计。该方法可以有效抑制脉冲性强的α 噪声，同时获得较好的时间分辨率和频率分辨率。

1 基本原理

1.1 分数低阶STFT

假定窗函数h（t）平稳，用h（t）截取非平稳信号x（t）并求出该时刻的傅里叶变换，沿着时间序列不断移动窗函数h（t），求出各个时刻的傅里叶变换，这一方法称为短时傅里叶变换［9］，即：

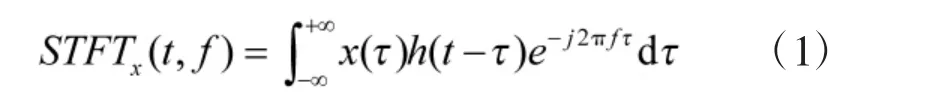
为更好地表征空间环境噪声中非高斯脉冲性特点，本文采用α 稳定分布噪声作为背景噪声模型。已知信号的统计矩作为识别信号特征的依据，是一种重要的数理统计量。假设随机信号的特征指数为α，则阶数大于α 的统计矩都是不存在的。若α稳定分布（0＜α＜2）的随机变量的p 阶矩为，其收敛性满足［9］：

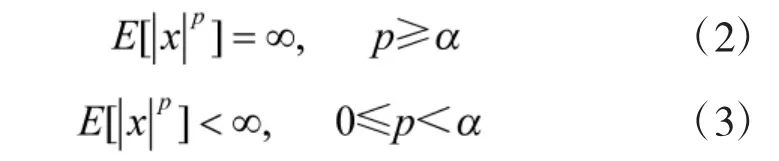
特别地，当α=2 时，

所以，α 稳定分布（0＜α＜2）的二阶矩以及二阶以上的高阶矩是不存在的，从而导致了基于二阶矩及高阶矩的信号分析方法（如STFT）会出现明显的性能下降乃至失效。基于此，分数低阶方法就成为了一种重要的时频分析手段。

若α 稳定分布（0＜α＜2）两个随机变量X 和Y满足1＜α≤2，共变［10］定义为：

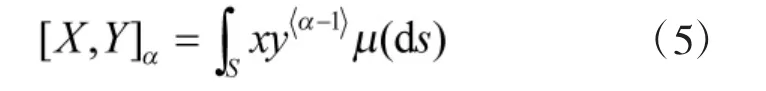
其中，S 表示单位圆；μ（·）为联合SαS 分布机变量X和Y 的谱测度；算子〈·〉表示如下运算：

共变仅适用于α 稳定分布满足1＜α≤2 的条件下，文献［11］提出了分数低阶协方差的概念，作为一种更一般的分数低阶统计量，对全部α 值均可适用。其定义为：

α 稳定分布（0＜α＜2）不存在二阶矩，但存在有限的p 阶矩（0＜p＜α）。若先将x（t）做p 阶的分数低阶算子运算，再做STFT，即可得到分数低阶STFT 的定义式：

由式（8）可知，FLOSTFTx（t，f）的时频性质是由x（t）的p 阶算子先通过加窗函数再做傅里叶变换得到的，而窗函数的长度直接影响了信号分析的准确性。通常情况下，窗长越短的窗函数，FLOSTFTx（t，f）的时间分辨率越高、频率分辨率越低；窗长越长的窗函数，FLOSTFTx（t，f）的时间分辨率越低、频率分辨率越高。对于给定的窗函数h（t），假设时窗中心为Δt，频窗中心为Δf，根据不确定性原理得到Heisenberg 不等式［12］：

通过式（9）可知，时域宽度和频域宽度不能取任意小，因此，分数低阶STFT 不可能得到任意高的时间分辨率和频率分辨率。

1.2 组合窗函数的分数低阶STFT

在分数低阶STFT 中，窗函数的选取是极其重要的。窗函数一经选择，在整个二维联合时频分析的所有局部域中，时间、频率的分辨率都是固定的，这也是分数低阶STFT 最大的不足。但是，通过研究不难发现，分数低阶STFT 有良好的能量聚集性。若假定非平稳信号x（t）的能量在时域集中于［-t，t］的时间间隔内，在频域集中于［-f，f］的频率间隔内，经分数低阶STFT，分数低阶STFT 的值将局域化在［-t，t］×［-f，f］上，而在其他区域内，分数低阶STFT的值趋近于零。基于此，本文提出了一种组合窗函数的分数低阶STFT 时频分析方法。

将式（8）离散化，得到离散的分数低阶STFT 表达式：

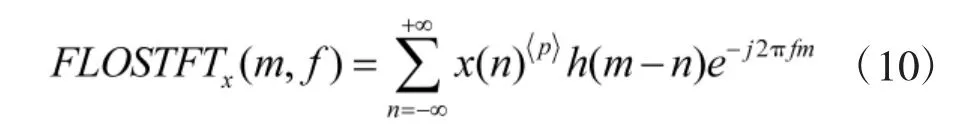
由式（10）可知，对于任意时刻的m，分数低阶STFT 可以看作对x（n）的p 阶算子作离散傅里叶变换。在M 点离散傅里叶变换下，可得到：

由式（11）可知，在N 值确定的情况下，经分数低阶STFT 变换后的数据维度就确定了下来，与窗函数的长度无关。

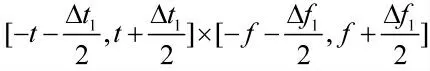
2 数学模型

2.1 标准SαS 分布的噪声模型

α 稳定分布没有固定的概率密度函数表达式，但存在固定的特征函数表达式［13］：

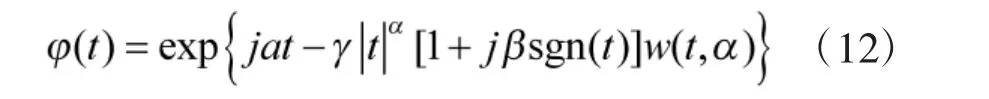
其中：

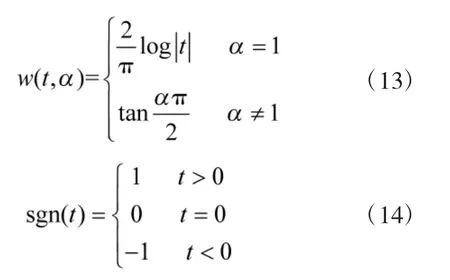
式（12）中，α∈（0，2］为特征参数，β∈［-1，1］为对称参数，γ＞0 为分散系数，a∈（-∞，∞）为位置参数，上述4 个参数确定了α 稳定分布的特征函数。由文献［13］可知，当β=0，γ=1，a=0 时，对应于标准SαS 分布。该分布的概率密度函数具有平滑、单峰分布、对称等特点，与空间环境中脉冲噪声信号的特征十分吻合。

文献［14］利用Deroye 方法得到标准SαS 分布的随机变量。具体步骤如下：

2）产生均值为1 的服从指数分布的随机变量W；

3）定义随机变量：

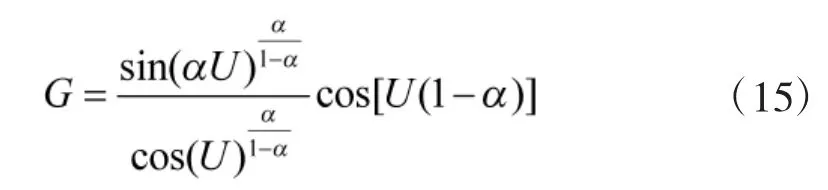
4）得到标准SαS 分布的随机变量：

由前文可知，低阶α 稳定分布（0＜α＜2）的二阶矩是不存在的，所以基于二阶统计量方差定义的信噪比不再适用，为表征信号与噪声的关系，引入广义信噪比［14］：

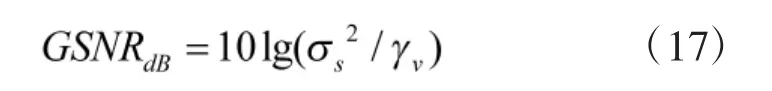
2.2 跳频信号的数学模型

跳频信号的数学模型可以定义为［15］：

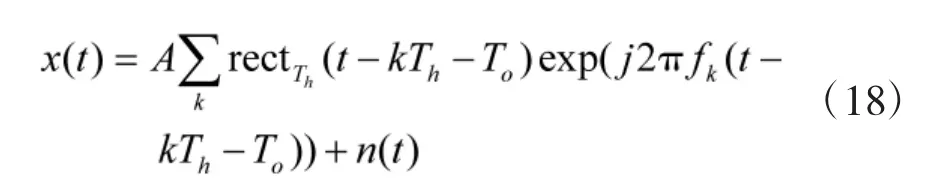
其中：

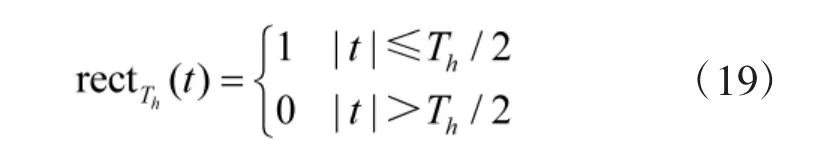
其中，A 为跳频信号的功率，Th为跳变周期，To 为跳变时刻，fk为第k 次跳变频率，rectT（ht）是高为1，宽为Th的闸门函数，n（t）为加性噪声，本文采用标准SαS 分布的α 稳定分布噪声作为背景噪声模型。

3 参数估计的基本步骤

本文采用基于时频分析的跳频参数估计方法，其核心思想是首先获得聚集性良好、有足够时频分辨率的时频分布，再进行参数估计。具体步骤归纳如下：

1）对跳频信号x（t）采样记作x（n），选取两个窗长不同的窗函数作为时间窗，对x（n）作分数低阶STFT 变换，得到结果记作TFR1（m，n），TFR2（m，n）；

2）TFR1（m，n）×TFR2（m，n）得到新的时频表示TFR（m，n）；

3）计算TFR（m，n）在每一个时刻m 点沿频率轴的最大值，得到矢量y（m）；

4）对y（m）作快速傅里叶变换，得到离散跳周期的估计值Ne，则跳周期的估计值Te=Ne/Fs；

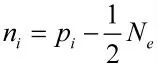
6）估计x（n）的跳频频率，得到跳频频率集：

图1 GSNR=3 dB 时不同α 值跳频信号时域图与频域图

4 仿真结果及分析

4.1 跳频信号的时频分布

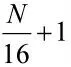
图2 跳频信号的三维时频分布图

从图2 中可以清楚地看到跳频信号时间、频率、幅度的三维分布情况。其中，凸起的峰值数目代表了跳频信号的数目，图中8 个波峰对应8 个跳频信号。凸起的峰值越尖锐，能量就越密集，说明算法的性能越好。图中，时间轴上的峰宽代表跳周期，峰值的变化时刻代表了信号的跳变时刻，频率轴的峰值代表了信号频率的大小。显然，在四组三维时频分布图中，分数低阶STFT 对脉冲噪声有抑制作用；而组合窗函数的分数低阶STFT 对脉冲噪声抑制效果更为显著，峰值更加尖锐，通过该算法获得的跳频信号特征参数值会有更好的性能指标。

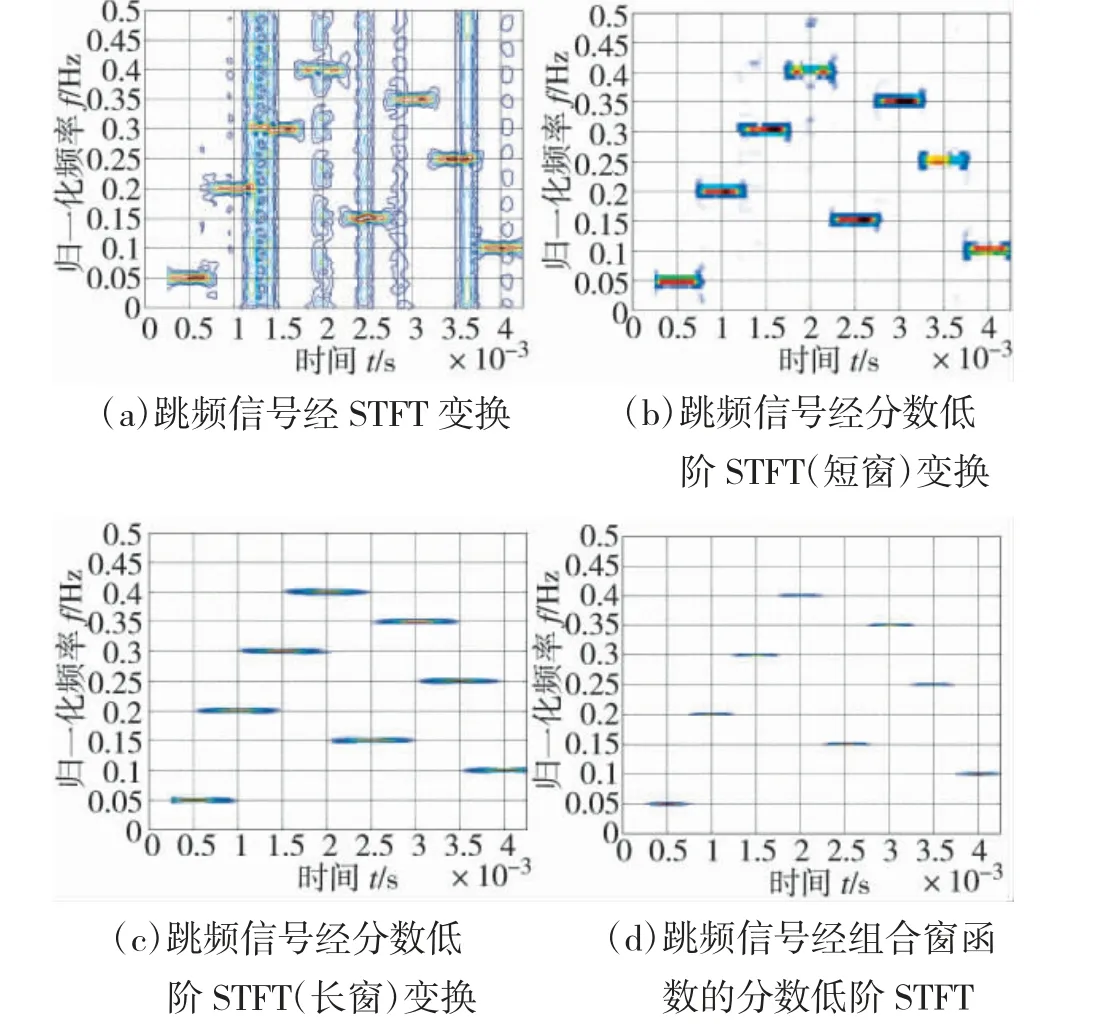
图3 跳频信号的等高线图

为了更直观地对不同时频分析方法作出比较，图3 给出了跳频信号的等高线示意图。图3（a）是跳频信号经STFT 变换所得的等高线图，由图可见，脉冲性的α 噪声使STFT 的时频分析能力大大减弱。图3（b）、图3（c）是不同窗长的分数低阶STFT 变换所得的等高线图，该方法对脉冲性的α 噪声有一定的抑制作用，但不能同时获得较好的时间分辨率和频率分辨率，图3（b）中短窗的分数低阶STFT 变换有较好的时间分辨率，图3（c）中长窗的分数低阶STFT 变换有较好的频率分辨率。图3（d）是组合窗函数的分数低阶STFT 变换所得的等高线图，可以直观地看到，该方法对脉冲性的α 噪声有显著的抑制作用，性能明显优于上述方法，并可以同时得到较好的时间分辨率和频率分辨率。

4.2 跳频信号的参数估计

根据上文中参数估计的基本步骤可知，跳变时刻、跳频频率集的参数估计均基于跳频周期的准确估计，故跳频周期的估计是特征参数估计的关键。基于上文仿真模型，α 值分别取1.5、0.8，将广义信噪比作为自变量，分别通过STFT、分数低阶STFT（应用时间分辨率更高的短窗）、组合窗函数的分数低阶STFT 对跳频信号进行参数估计，经500 次蒙特卡洛实验，得到不同α 值跳频周期的均方误差如下页图4 所示。

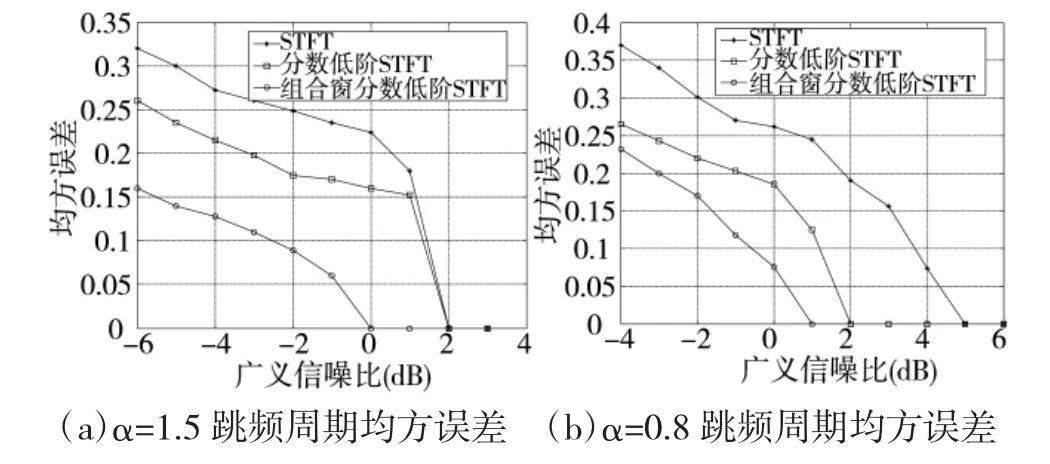
图4 GSNR=3 dB 时不同α 值跳频周期均方误差

由图4（a）可知，对于α=1.5 的标准SαS 分布噪声，采用组合窗函数的分数低阶STFT 在GSNR≥0 dB时，可以准确地估计出跳频周期；采用分数低阶STFT 和STFT 在GSNR≥2 dB 时才可以达到准确估计跳频周期的效果，同时，这也说明了在α=1.5 的条件下，对于脉冲性不强的噪声信号，STFT 仍可适用。另一方面，在GSNR＜0 dB 时，采用组合窗函数的分数低阶STFT 得到的均方误差更小，进一步体现了该算法对跳频周期的参数估计性能优于分数低阶STFT 和STFT。由图4（b）可知，对于α=0.8 的标准SαS 分布噪声，采用组合窗函数的分数低阶STFT在GSNR≥1 dB 时，可以准确地估计出跳频周期；采用分数低阶STFT 在GSNR≥2 dB 时才可以达到准确估计跳频周期的效果；采用STFT 性能严重退化，在很大广义信噪比前提下才能对跳频周期有效估计。另一方面，在不同广义信噪比条件下，组合窗函数的分数低阶STFT 得到的均方误差更小，算法性能优于分数低阶STFT 和STFT。同时比较图4（a）和图4（b），不难发现，随着α 值的减小，几种算法的跳频周期均方误差都会增大，估计性能下降；另一方面，组合窗函数的分数低阶STFT 算法性能优于分数低阶STFT 和STFT。

对跳频周期估计后，根据步骤5 对跳变时刻进行有效估计。通过前文可知，在GSNR=3 dB 且α=1.5时，3 种方法均可准确估计跳频周期，为比较3 种情况下对跳变时刻、跳频频率的估计性能，本文在GSNR=3 dB 且α=1.5 的情况下采用STFT、分数低阶STFT、组合窗函数的分数低阶STFT 分别进行500次蒙特卡洛实验，所得的跳变时刻估计如表1 所示。

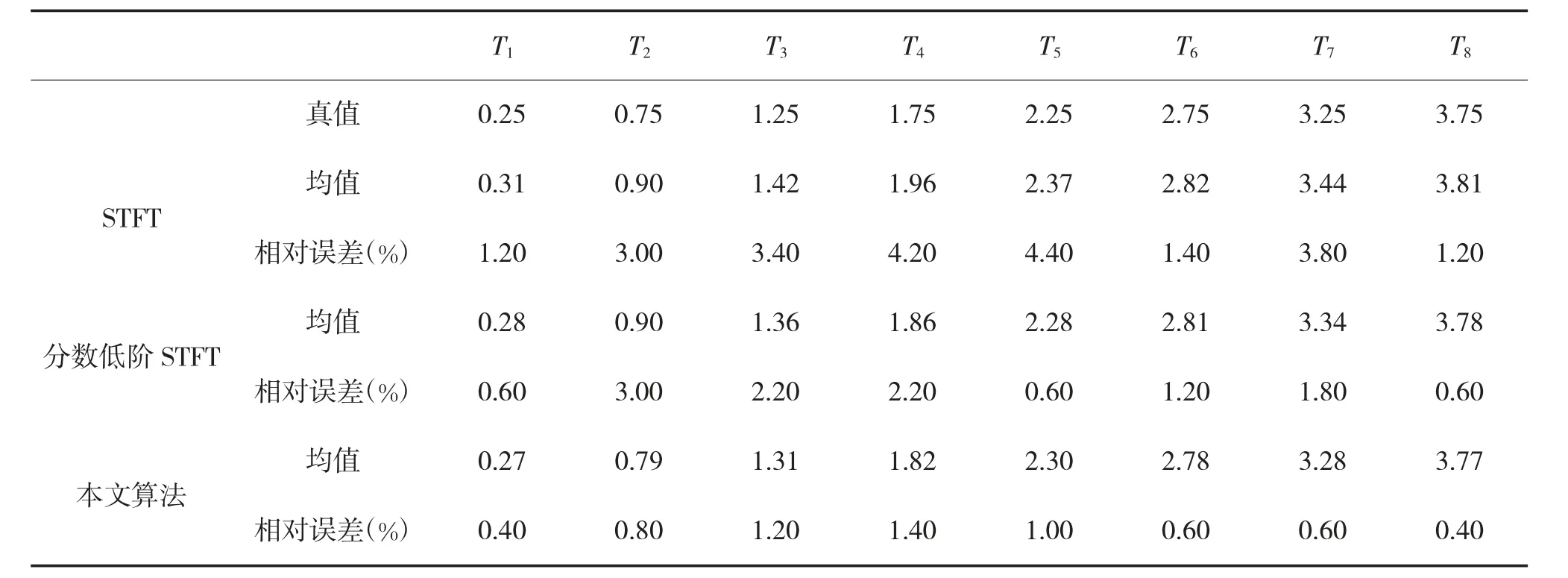
表1 不同算法跳变时刻 单位：ms

由表1 可知，采用STFT 对跳变时刻进行参数估计，最大相对误差为4.40%，即跳变时刻的误差不超过0.22 ms；采用分数低阶STFT 跳变时刻进行参数估计，最大相对误差为3.00%，即跳变时刻的误差不超过0.15 ms；采用组合窗函数的分数低阶STFT跳变时刻进行参数估计，最大相对误差1.40%，即跳变时刻的误差不超过0.07 ms。可见，对跳变时刻的估计，组合窗函数的分数低阶STFT 算法性能优于分数低阶STFT 和STFT。

对跳变时刻估计后，根据步骤6 对跳频频率进行有效估计。表2 为估计结果。由表2 可知，应用组合窗函数的分数低阶STFT 所得的跳频频率值比分数低阶STFT 和STFT 更为精确。

综上所述，在跳频信号的特征参数估计中，组合窗函数的分数低阶STFT 算法性能优于分数低阶STFT 和STFT。

表2 不同算法跳频频率 单位：kHz

5 结论

本文针对在α 稳定分布噪声环境下，传统的分析方法以及分数低阶STFT 的不足，提出了组合窗函数的分数低阶STFT 方法，该方法能够同时获得长窗函数的频率分辨率和短窗函数的时间分辨率，在较低的广义信噪比环境下，有效实现了对跳频信号时频分析。仿真实验表明，本文方法可以有效地抑制脉冲噪声，在广义信噪比较低的环境下完成跳频信号的参数估计，且算法性能优于分数低阶STFT和STFT，在信号截获分析领域中具有一定的工程应用价值。