湖南省怀化市铁路第一中学

近年来求多面体的外接球问题在高考试题、各地模拟试题中频频出现,成为了热点问题,其中四面体的外接球问题最具代表性.求四面体外接球问题的两种常用方法一是截面法,即找球心求半径;二是补形法,即将四面体补成长方体(四面体的所有顶点均为长方体的顶点),也就是等价转化为求长方体的外接球问题.通过检索大量的文献发现,写四面体外接球问题的文章不少,而且必然会提到上述两种常用解法.关于补形法,绝大多数文章都只是列举几种常用的可以补成长方体的四面体,普遍存在类型不全、归类不准确、重复等问题,而且没有给出严格的数学证明.那么,到底什么样的四面体能够补成长方体呢?

类型一“墙角”四面体(过某顶点的三条棱两两垂直)

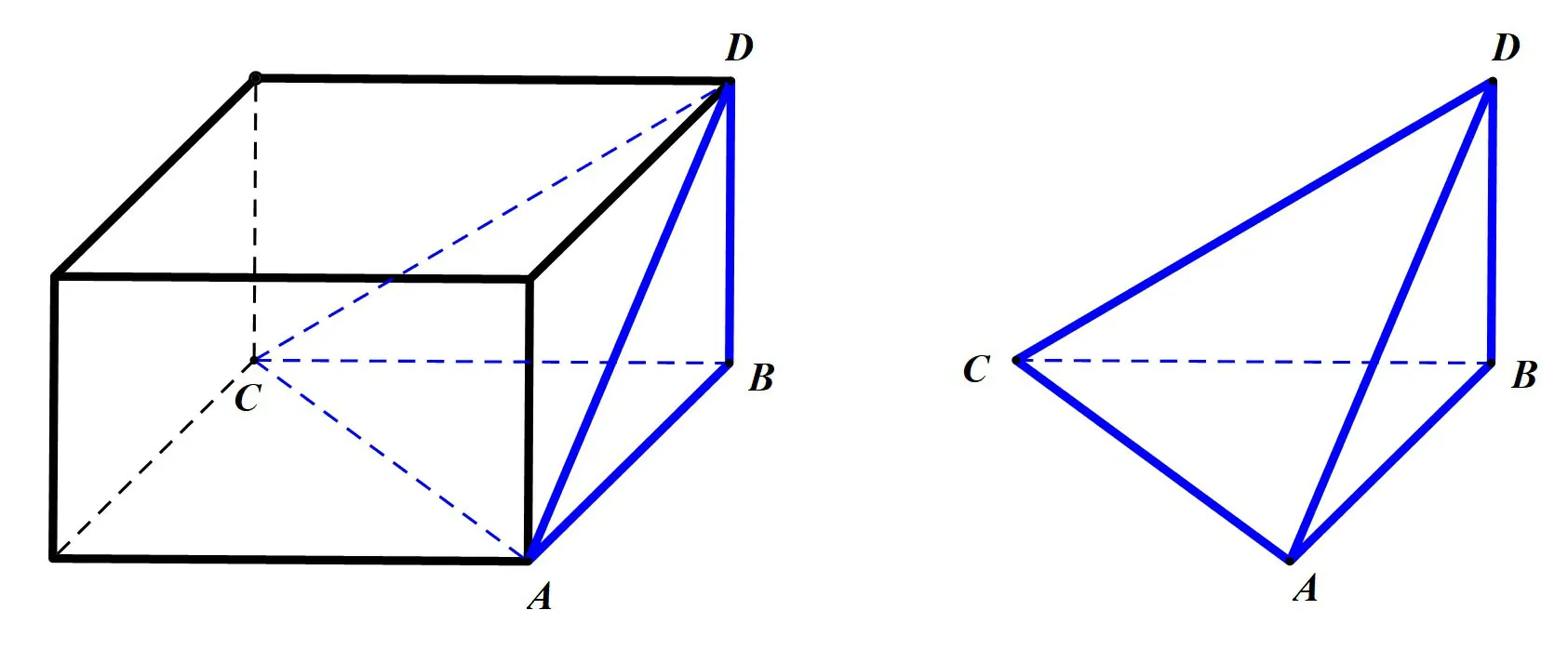
图1

结论1过某顶点的三条棱两两垂直的四面体能补成长方体.

结论1 是显然成立的.如图1,四面体ABCD可以补成以AB、BC、BD为长、宽、高的长方体.

例1(2019年高考全国Ⅰ卷理科第12题)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,ΔABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为()

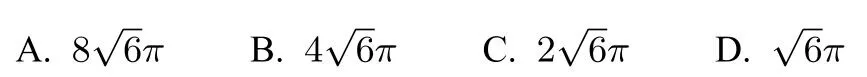
解析如图2,因为CE ⊥EF,所以CE ⊥PB.作AC的中点G,连接PG、BG,由于PA=PC,ΔABC是正三角形,则AC ⊥PG,AC ⊥BG,从而AC ⊥平面PGB,所以AC ⊥PB.

图2

又AC ∩CE=C且AC,CE ⊂平面PAC,所以PB ⊥平面PAC,则ΔPAB,ΔPAC为等腰直角三角形,得PA=PC=又AC=2,所以PA ⊥PC.从而,三棱锥P-ABC过点P的三条棱PA,PB,PC两两垂直,所以可以补成以PA,PB,PC为长宽高的长方体(实际上是正方体),则外接球半径外接球的体积为

评注此题通过所给条件可以得到三棱锥P-ABC过点P的三条棱PA,PB,PC两两垂直,即三棱锥P-ABC是个“墙角”四面体.于是由结论1 可以将三棱锥补成正方体,转化为正方体的外接球问题,正方体的体对角线即是其外接球的直径,从而使得问题的求解变得极为简便.

类型二“鳖臑”四面体(四个面均为直角三角形)

《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.

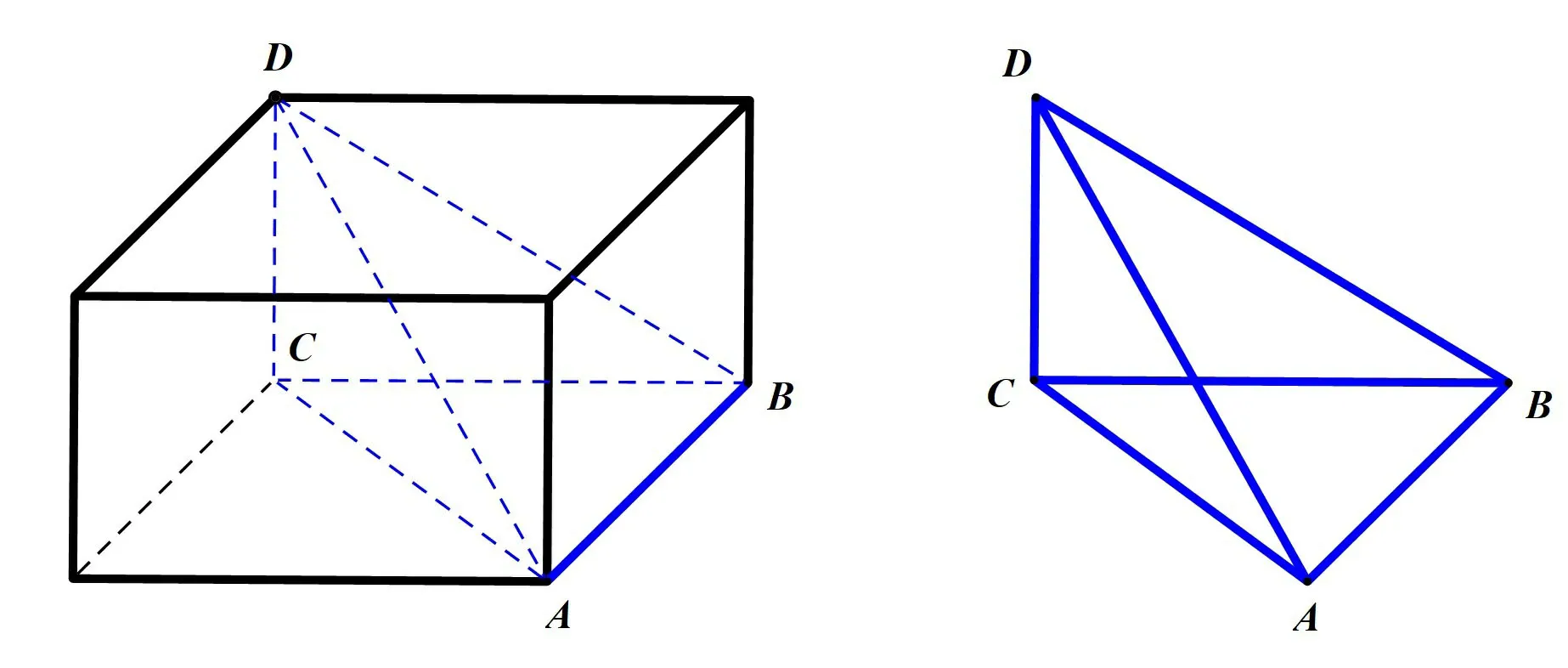
图3

结论2四个面均为直角三角形的四面体的能补成长方体.

结论2 也是显然成立的.如图3,四面体ABCD可以补成以AB、BC、CD为长、宽、高的长方体.

例2(2008年高考浙江卷第14题)如图4,已知球O点面上四点A,B,C,D,DA ⊥平面ABC,AB ⊥BC,DA=AB=BC=则球O的体积等于____.

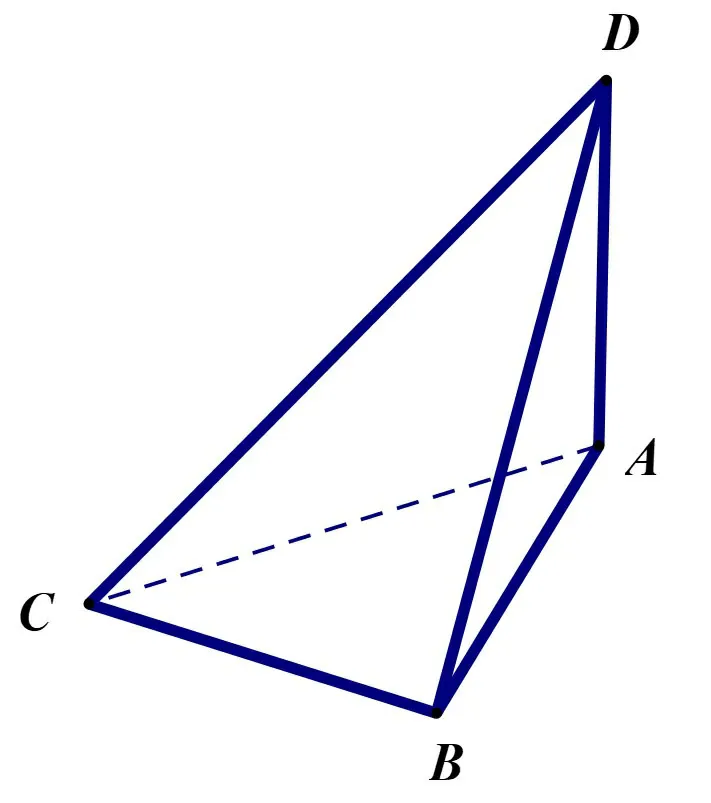
图4

解析 球O为四面体ABCD的外接球.因为DA ⊥平面ABC,则ΔABD、ΔACD为直角三角形,且DA ⊥BC,又AB ⊥BC,得到BC ⊥平面ABD,从而BC ⊥BD,所以ΔABC、ΔBCD也是直角三角形,则四面体ABCD四个面均为直角三角形,即四面体为“鳖臑”四面体,所以能补成以AB、BC、AD为长、宽、高的长方体,其外接球的直接为长方体的体对角线,则球O半径为于是球O的体积为

评注通过研究四面体的线面关系,发现四面体的四个面均为直角三角形,即为“鳖臑”四面体,由结论2 知,该四面体能补成长方体,于是不难求出其外接球的体积.

类型三 对棱相等的四面体

图5

结论3对棱相等的四面体能补成长方体.

证明设四面体ABCD三组对棱长分别为x、y、z,要证四面体ABCD能补成长、宽、高分别为a、b、c的长方体,则只要证方程组有解,变形得故只要证即只需证明四面体ABCD的四个面为锐角三角形.

因为四面体ABCD的对棱相等,则四个面是四个全等三角形,令a、b、c的对角分别为α、β、γ则α+β+γ=180°.任取一顶点,考虑由α、β、γ组成一个三面角,在三面角中,任意两面角之和大于第三个面角,所以α < β+γ,则2α<α+β+γ=180°,所以α<90°,即α为锐角.同理可证明β、γ均为锐角.这就证明了四面体ABCD的四个面为锐角三角形,从而证明了对棱相等的四面体能够补成长方体.事实上,正四面体能补成正方体只是类型三的特殊情况.

例3(2018年全国高中数学联赛浙江预赛第10题)在四面体P-ABC中,已知则四面体的外接球半径是____.

解析不难发现四面体P-ABC的三对对棱相等,则可以将该四面体补成长方体,假设补成的长方体的长、宽、高分别为x、y、z,则于是长方体的外接球半径也即四面体P-ABC的外接球半径.

评注此题的突破口在于发现四面体P-ABC的三对对棱相等,由结论3,将四面体补成长方体,利用长方体的对角线求四面体的外接球半径.

类型四 有三个面为直角三角形且所有直角三角形的斜边为一组对棱的四面体

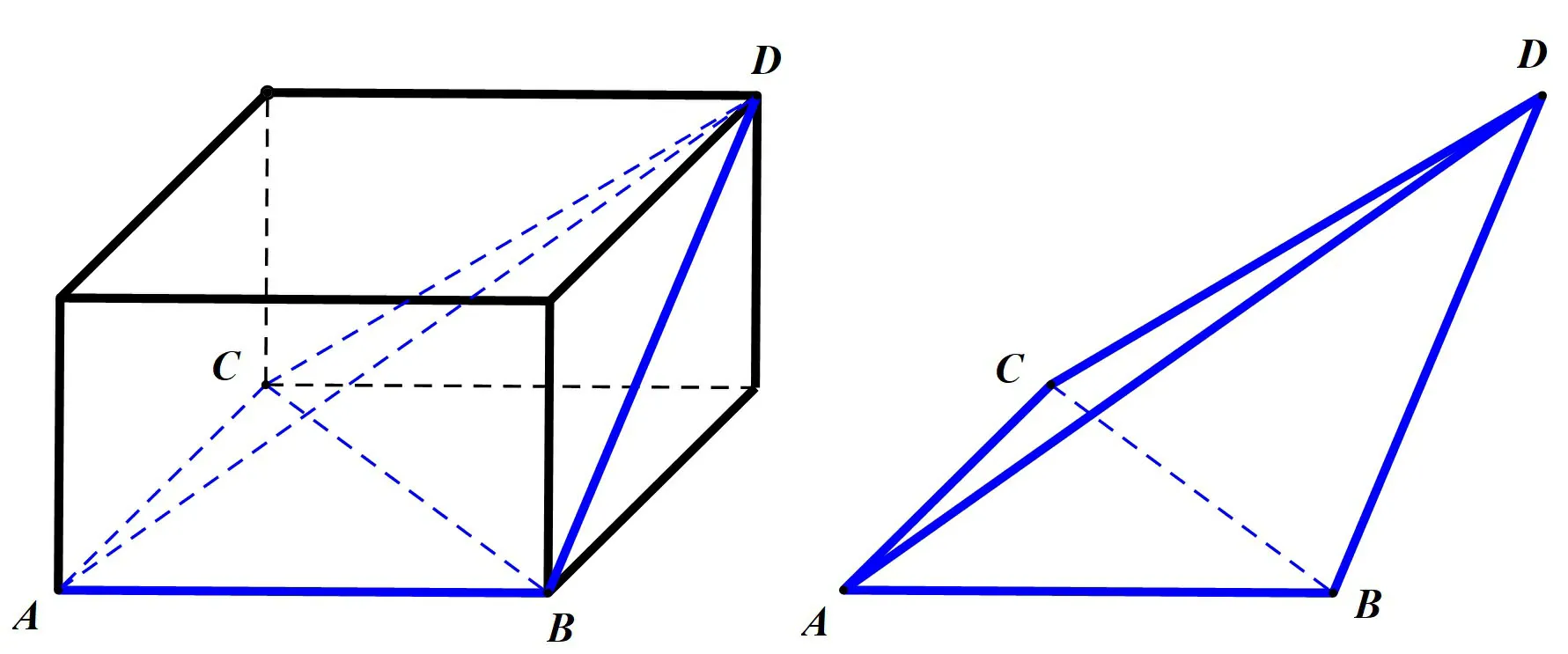
图6

结论4有三个面为直角三角形且所有直角三角形的斜边为一组对棱的四面体能补成成方体,且其中最长的棱(其中两个直角三角形的公共斜边)为长方体的体对角线.

证明1如图6,对棱AD、BC为直角三角形的斜边,且AB ⊥AC,AB ⊥BD,AC ⊥CD.设AB=a,AC=b,BC=x,BD=y,CD=z,要证四面体ABCD能补成的长、宽、高分别为a、b、c的长方体,只要证方程组有解,变形为因为AB ⊥AC,AB ⊥BD,AC ⊥CD,有a2+b2=x2,a2+y2=b2+z2,两式相加得2a2=x2+z2-y2,两式相减得2b2=x2+y2-z2.那么只要证2c2=y2+z2-x2,即只需证y2+z2-x2>0,只要证明∠BDC为锐角即可.

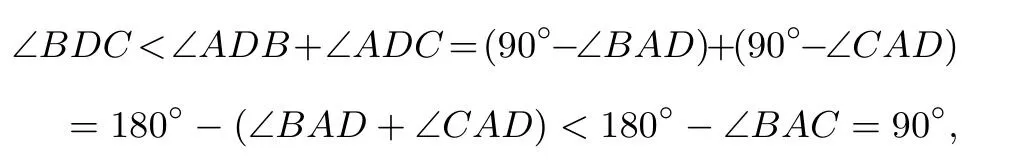
即∠BDC为锐角.这就证明了有三个面为直角三角形且所有直角三角形的斜边为一组对棱的四面体能补成方体.不难看出,四面体的棱AD即为长方体的体对角线.

证明2如图7,过点D作平面ABC的垂线DE,垂足为E,则DE ⊥AB,DE ⊥ AC.又因为AB ⊥BD,AC ⊥CD,而BD,DE ⊂平面BDE,且BD ∩DE=D;CD,DE ⊂平面CDE,且CD ∩DE=D.所以AB ⊥平面BDE,AC ⊥平面CDE,则AB ⊥BE,AC ⊥CE.

图7

所以四边形ABEC为矩形,从而可以补成以AB、AC、DE为长、宽、高的长方体.此时AD即为长方体的体对角线.

从检索到的文献来看,几乎都没提及类型四的四面体,唯文[1]将这种类型的四面体表述为“有不共点的相互垂直的三条棱”,不准确.文章也只粗略地给出了图示,并没给出这种类型的四面体能补成成方体的严格证明.

例4 如图8所示,四面体ABCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD==CD=1,另一个侧面ABC是正三角形,则四面体ABCD的外接球的侧面积为.

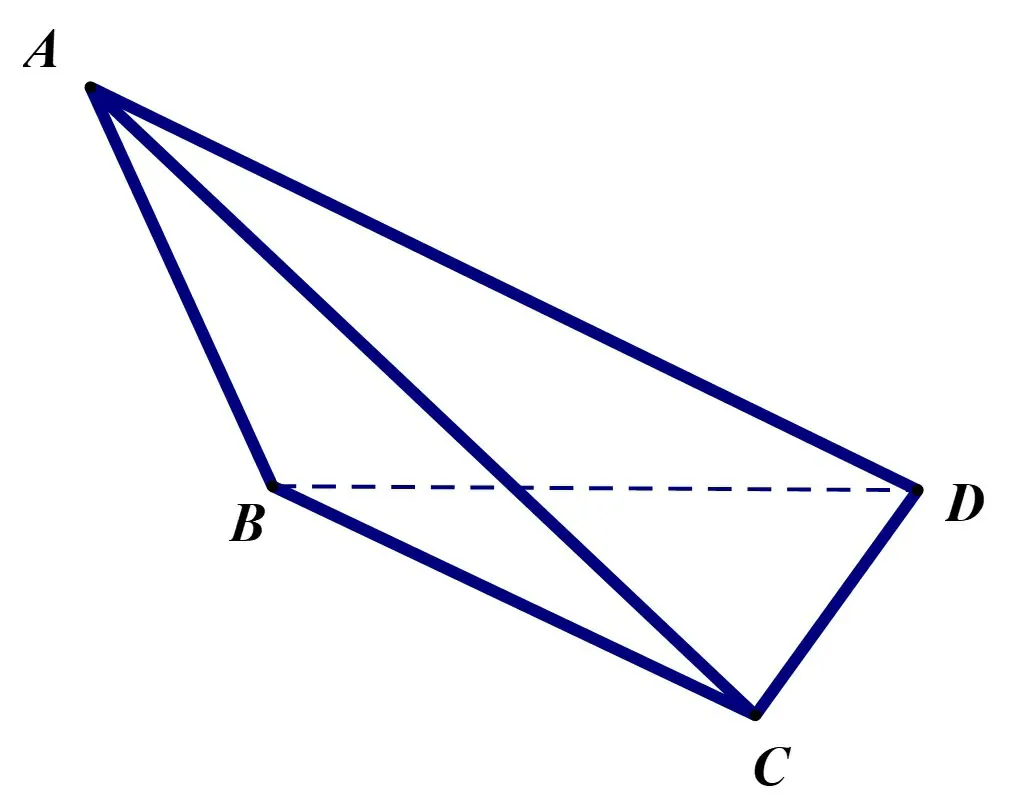
图8

解析因为BC=AB=所以ΔBCD也是直角三角形,且斜边为BC,从而四面体ABCD中有三个直角三角形ΔABD、ΔACD、ΔBCD,且所有的直角三角形的斜边为四面体的一组对棱AD、BC,所以该四面体能够补成长方体,且棱AD为长方体的体对角线.故四面体的外接球半径为其外接球表面积为S=4πr2=3π.

评注通过分析四面体的棱长,发现了三个直角三角形且所有直角三角形的斜边为一组对棱,由结论4 知该四面体能补成长方体,于是问题由此得解.

另一方面,除了上述四种类型的四面体外还有其他的四面体能补成长方体吗? 为了解除这个疑问,可以换个角度来思考,看看从长方体中可以取出哪些类型的四面体?

由对称性,在长方体中取四面体只有两种情况:一是在一对对面上其中一个面上取三个顶点,另一个面上取一个顶点;二是在一对对面上各取两个顶点.

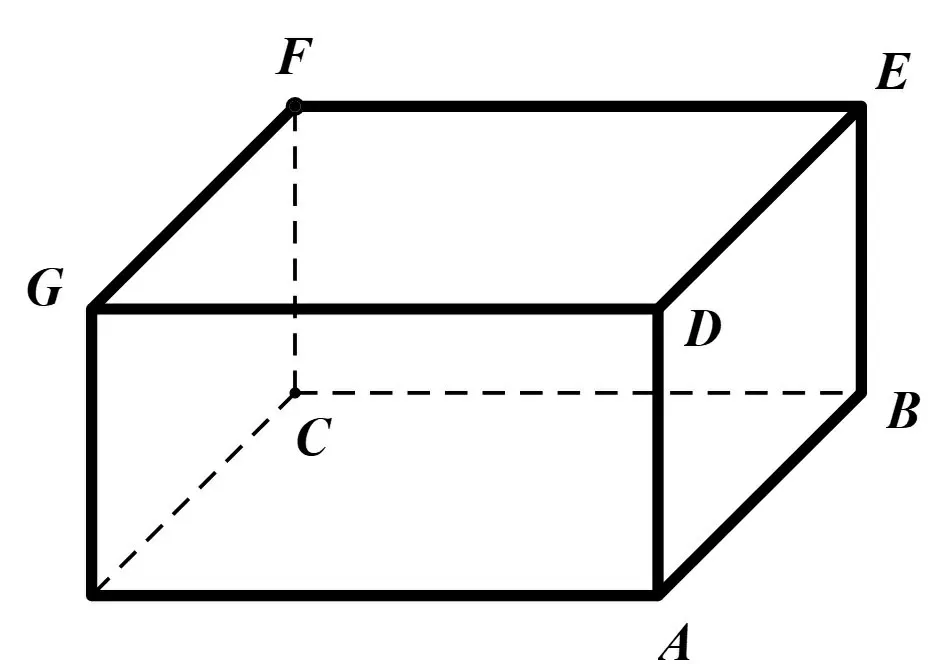
图9

情况一:如图9,在底面上取三个顶点A、B、C,则ΔABC必为直角三角形,若在其对面上取顶点E,得到的四面体就是类型一;若在其对面上取顶点D或F,得到的四面体就是类型二;若其对面上取顶点G,得到的四面体就是类型四.

情况二:在一对对面上各取两个顶点,则各面上所取得两顶点必在该面的对角上,否则与情况一重复.如图9,在底面上取两顶点A、C,则在对面上只能取顶点E、G,此时得到的四面体就是类型三.

综上所述,从长方体中只能取出上述的四类四面体,所以以上四类四面体即为所有能够补成长方体的四面体.

总结 只有以上四种类型的四面体能够补成长方体.所以,在求解四面体外接球问题时,如果符合以上四种类型,则可以补成长方体,利用长方体体对角线求外接球半径,会使得问题的求解更为简便;否则,只能通过其他方法求解.