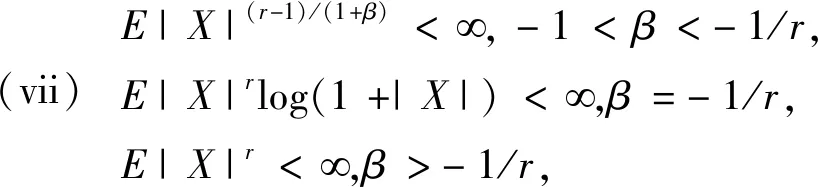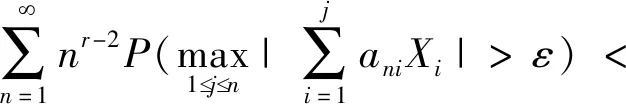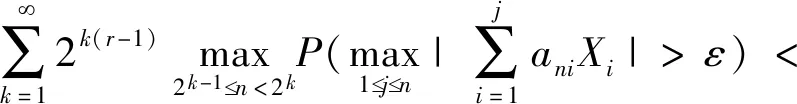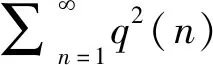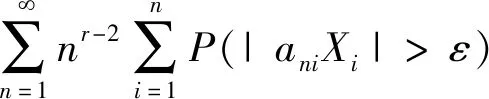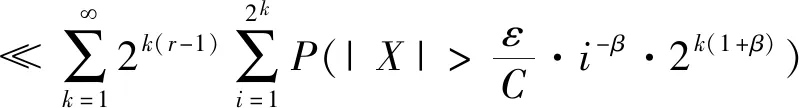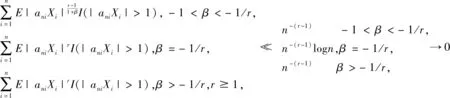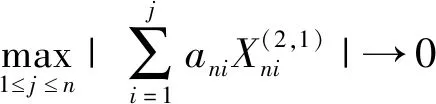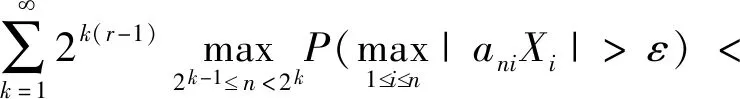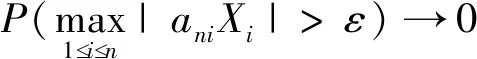(厦门工学院计算机与人工智能学院数学系,福建 厦门 361021)

0 引 言

AANA序列由Chandra和Ghosal[1,2]提出，是一类广泛的负相依序列，包含NA序列(当q(n)=0,n≥1时)及一些很接近NA序列的随机变量序列，是更为普遍、应用更为广泛的一类随机变量序列，对其进行研究是有价值的. 下面考虑一类被随机控制的AANA序列，利用相应的Rosenthal型不等式(引理1.2)讨论其加权和的矩完全收敛性定理，并得到其完全收敛性成立的若干条件.

1 定义与引理

定义1.1[1,2]称{Xn,n≥1}为AANA序列，若存在非负序列q(n)→0(n→0)，使得对任意n,k≥1, 有Cov(f(Xn),g(Xn+1,…,Xn+k))q(n)[Var(f(Xn))Var(g(Xn+1,…,Xn+k))]1/2,这里f和g是对每个变量均非降连续，且使得上式中方差和协方差都存在的函数.

定义1.2 称随机变量序列{Xn,n≥1}是由随机变量X随机控制的，若存在常数C>0，使得对任意x≥0，有supn≥1P(|Xn|>x)CP(|X|>x).

为证明主要结论，这里需要用到如下引理：

引理1.1[3]设{Xn,n≥1}是混合系数为{q(n),n≥1}的AANA序列，若{fn,n≥1}是非降(或非增)的连续函数，则{fn(Xn),n≥1}仍是混合系数为{q(n),n≥1}的AANA序列.

引理1.3 设{Xn,n≥1}是混合系数为{q(n),n≥1}的AANA序列，{ani,1in,n≥1}是实数阵列. 若，则对任意x≥0，n≥1，存在正数C使得

证引理1.3的证明与文献[4]中类似，在此省略.

引理1.4[4]设{Xni,1in,n≥1}为三角阵列随机变量序列. 令τ>0，{an,n≥1}和{bn,n≥1}为正数序列. 若对任意ε>0都有，则对任意ε>0，有

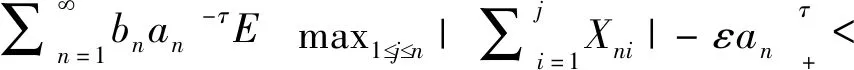
2 主要结论与证明

定理2.1 设{Xn,n≥1}是混合系数为{q(n),n≥1}的AANA序列，且被随机变量X随机控制. 令r>1,θ>0,β>max{-1,-1/θ},p>max{0,(1-θ)/(r-1)}，且当β>-1/2时p<2(1+θβ)/(1+2β)，r>max{1,(3-θ+3β)/[2(1+θβ)]}. 设{ani=cniiβn-(1+θβ)/p,1in,n≥1}是常数三角阵列，满足对任意1in,n≥1，存在正数C，使|cni|C. 若

则对任意ε>0，

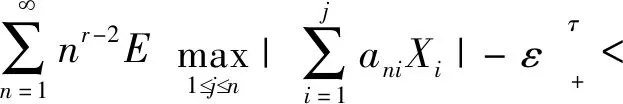
(1)

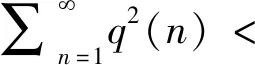
若r≥2，|cni|≥c(∀1in,n≥1)，这里c为一正数，且存在ε>0,τ>0使得(1)成立，则(ii)成立. 若还有(i)和(iii)成立，且对任意n≥1有c|cni|则E(X)=0.

证由引理1.2-引理1.4，利用和文献[5]类似的方法可以证明，这里省略.

定理2.2 设{Xn,n≥1}是混合系数为{q(n),n≥1}的零均值AANA序列，且被随机变量X随机控制. 令r>1，β>-1. 设{ani=cni·(i/n)β·(1/n),1in,n≥1}是常数阵列，满足0

则对任意ε>0有

(2)

(3)

(4)

(5)

证由定理2.1，取p=θ=1即可得(2).又注意到

(6)

即得(3)和(4).

D1<可由(4)和以下不等式得到

D1

至于D2，由EXn=0(∀n≥1)和(vii)，有

由Markov不等式，(viii)，引理1.2，Cr不等式及Jensen不等式，可得

注意到

类似(6)式的证明，由(vii)和(viii)可得M1<和M2<，故(5)成立.

反过来，当10使得(5)成立，则

(7)

由于AANA序列包含NA序列(q(n)=0时)，故文献[6]和[7]的结论都可作为定理2.1的特例，且文献[7]中Cni的范围也得到扩展. 定理2.2采用不同方法得到文献[5]类似结论，过程更为简洁。