吴 江，韩丹夫

(杭州师范大学理学院，浙江 杭州 311121)

近几十年来，数值分析的研究工作因为计算机的快速发展而得到了大幅度推进.非线性方程求解是数值分析中极其重要的研究内容.许多应用技术问题，如物理、工程技术等，都涉及到非线性方程问题，所以求解非线性方程是工程计算中非常重要的内容.迭代法是求解非线性方程最常用的方法，其中牛顿迭代法最为常用.

在牛顿迭代法和其他经典的迭代法被广泛地应用后, 多位学者以牛顿迭代法为基础，构造了许多改进的迭代法[1-9]，以此来提高迭代法的收敛阶和收敛效率.笔者以牛顿迭代法和算术平均牛顿法为基础，构造收敛阶更高的迭代法，以进一步提高迭代法的计算效率.

1 牛顿迭代法

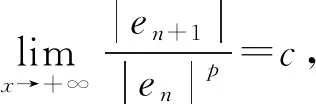
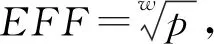
牛顿迭代法的迭代格式为

算术平均牛顿法是在牛顿迭代法基础上改进的迭代法，迭代格式为：

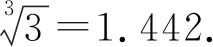
2 两种具有六阶收敛速度的迭代格式

在这一章中，以牛顿迭代法和算术平均牛顿法为基础，构造了两种六阶收敛的迭代格式，在提高收敛速度的同时，尽可能减少每步迭代所需计算的函数值和导数值个数，以此来保证迭代法的效率指数.

2.1 迭代格式

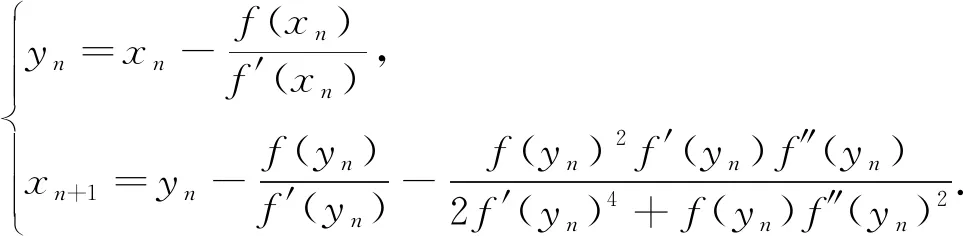
(1)

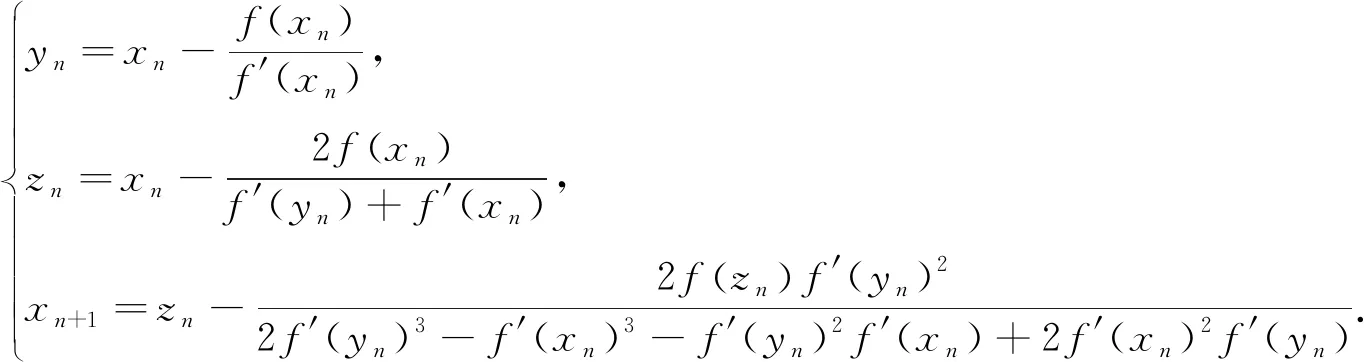
(2)

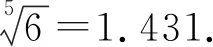
2.2 收敛性分析

定理1设方程f(x)=0的一个单根为a，函数f(x)在包含a的一个开区间I中充分光滑，当x0充分靠近a时，则式(1)所定义的迭代法在开区间I中以六阶收敛速度收敛于a，且其误差方程为

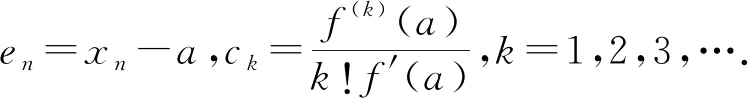
证明将f(xn)和f′(xn)在a处使用泰勒公式展开：

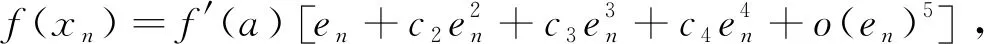
(3)

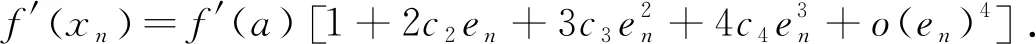
(4)

由式(3)、(4)得到

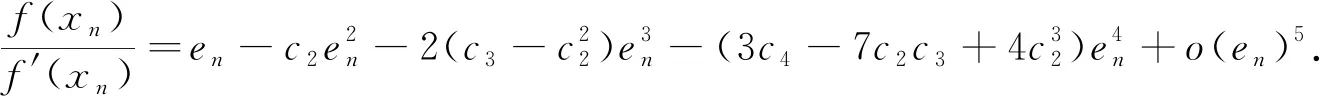
(5)

由式(5)得

(6)

利用式(6)，将f(yn)，f′(yn)以及f″(yn)在a处使用泰勒公式展开：

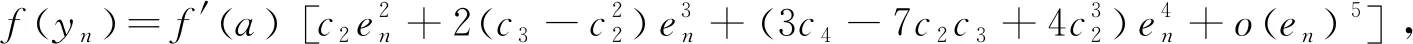
(7)

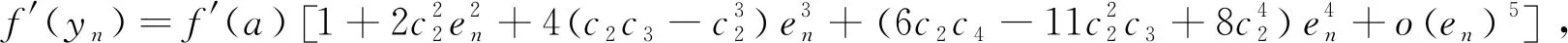
(8)

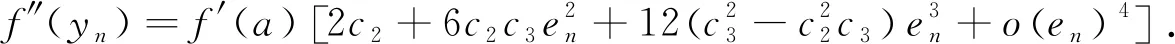
(9)

由式(6)、(7)、(8)得到

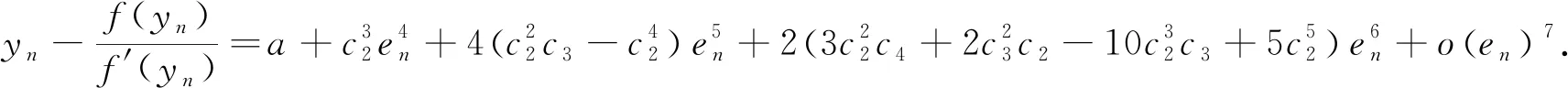
(10)

由式(7)、(8)以及式(9)得到

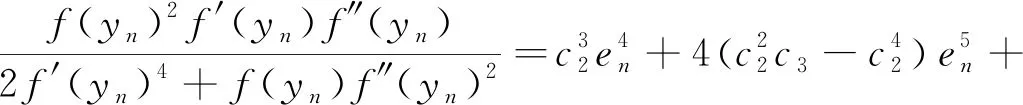
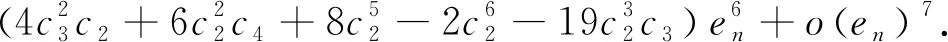
(11)

由式(10)、(11)得

进而有

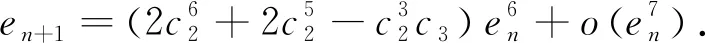
(12)

所以由式(12)知道迭代法(1)是具有六阶收敛速度的迭代格式.

定理2设方程f(x)=0的一个单根为a，函数f(x)在包含a的一个开区间I中充分光滑，当x0充分靠近a时，则式(2)所定义的迭代法在开区间I中以六阶收敛速度收敛于a，且其误差方程为

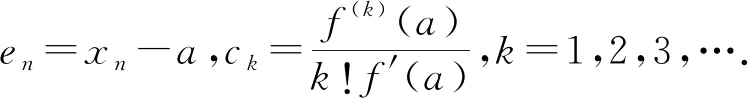
证明将f(xn)和f′(xn)在a处使用泰勒公式展开：

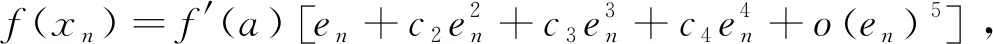
(13)

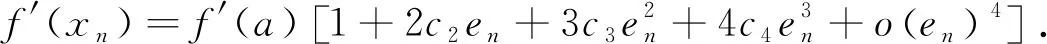
(14)

由式(13)、(14)得到

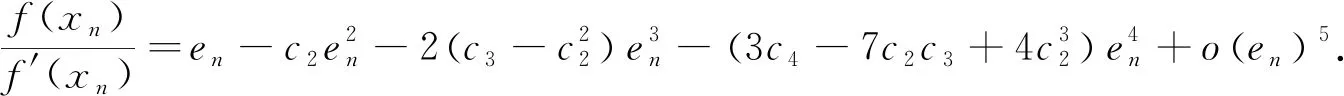
(15)

由式(15)得

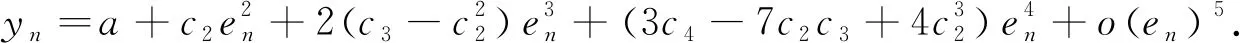
(16)

利用式(16)，将f(yn)以及f′(yn)在a处使用泰勒公式展开：

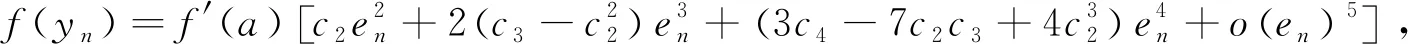
(17)

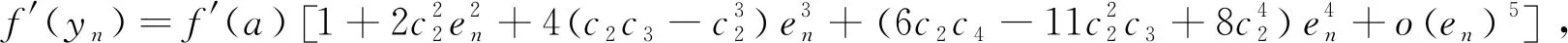
(18)

由式(13)、(14)以及式(18)得到

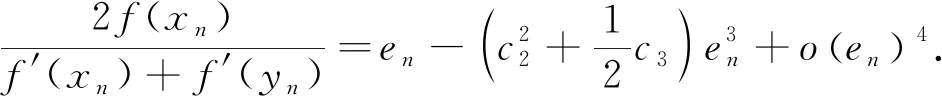
(19)

由式(14)、(18)得

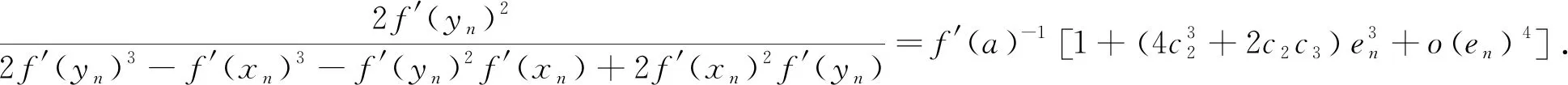
(20)

将f(zn)在a处使用泰勒公式展开，得到

f(zn)=f′(a)[(zn-a)+c2(zn-a)2+o((zn-a)3)].

(21)

由式(20)、(21)有

(22)

由式(19)得到

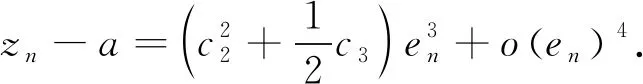
(23)

由式(22)、(23)得到

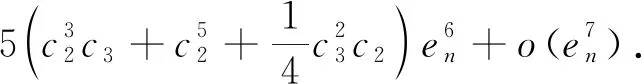
(24)

由式(24)知道迭代法(2)是具有六阶收敛速度的迭代格式.

3 数值实验

为验证新构造迭代法的有效性，将上述构造的两个六阶迭代法与牛顿迭代法和算术平均牛顿法进行比较.数值实验使用MATLAB2016b进行，精度设置为1 024位(digits =1 024).使用的测试函数如下：

f1(x)=x5-2x-8,a=1.622 528 493 002 836.

f2(x)=ex-10,a=2.302 585 092 994 046.

f3(x)=cos(x)-x,a=0.739 085 133 215 161.

f4(x)=x3+ex-x+sin(x),a=-0.809 586 035 891 489.

各个测试函数的数值实验结果列于表1至表4.表中以NM表示牛顿迭代法，AN表示算术平均牛顿法，MH1表示迭代法(1)，MH2表示迭代法(2)，x0表示迭代初值.每一个测试函数选取两个迭代初值，迭代停止条件为|xn-xn-1|<10-15，并输出误差值，n表示迭代次数，xn表示迭代结束后得到的近似零点.

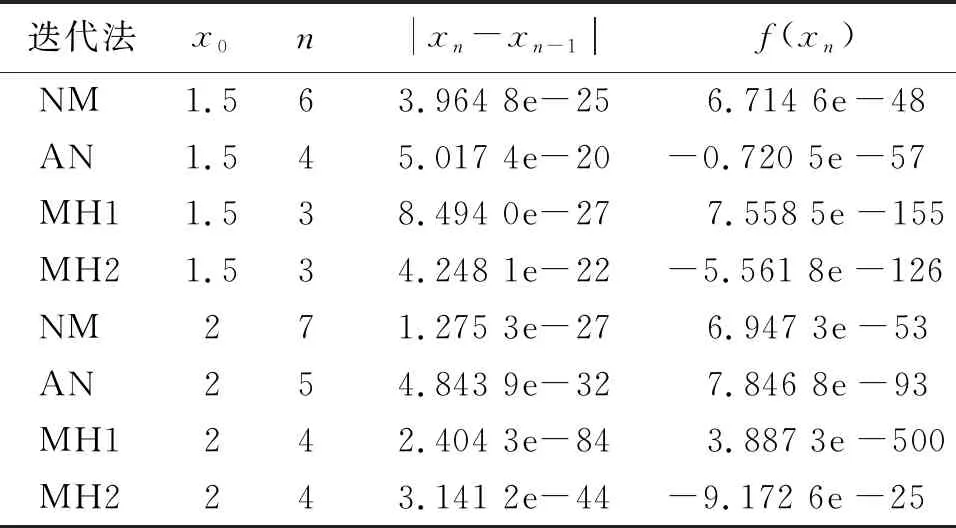
表1 测试函数为f1(x)的数值实验Tab.1 Numerical experimental results of test function f1(x)

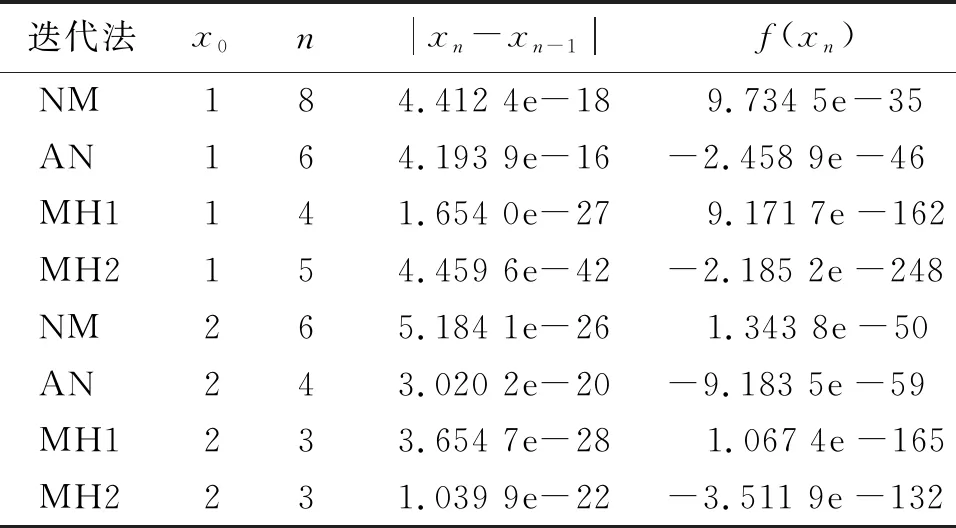
表2 测试函数为f2(x)的数值实验Tab.2 Numerical experimental results of test function f2(x)

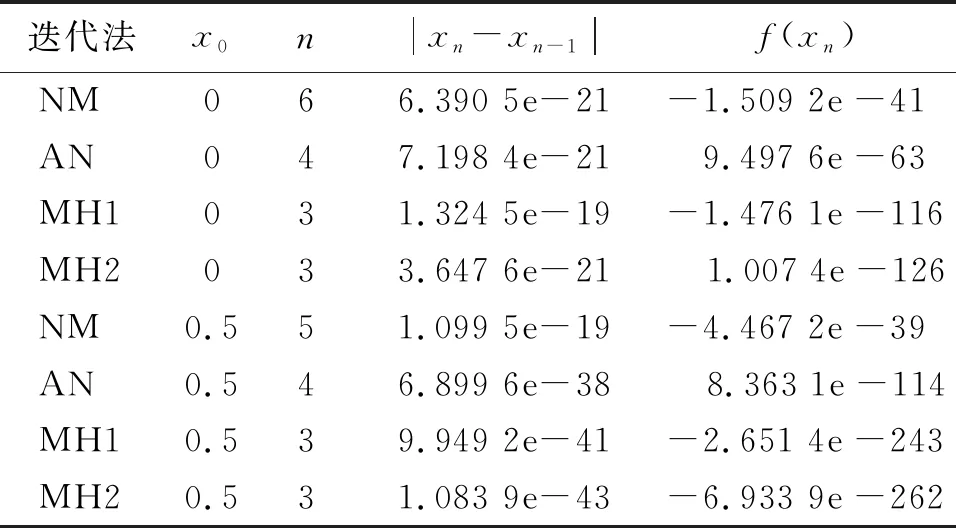
表3 测试函数为f3(x)的数值实验Tab.3 Numerical experimental results of test function f3(x)

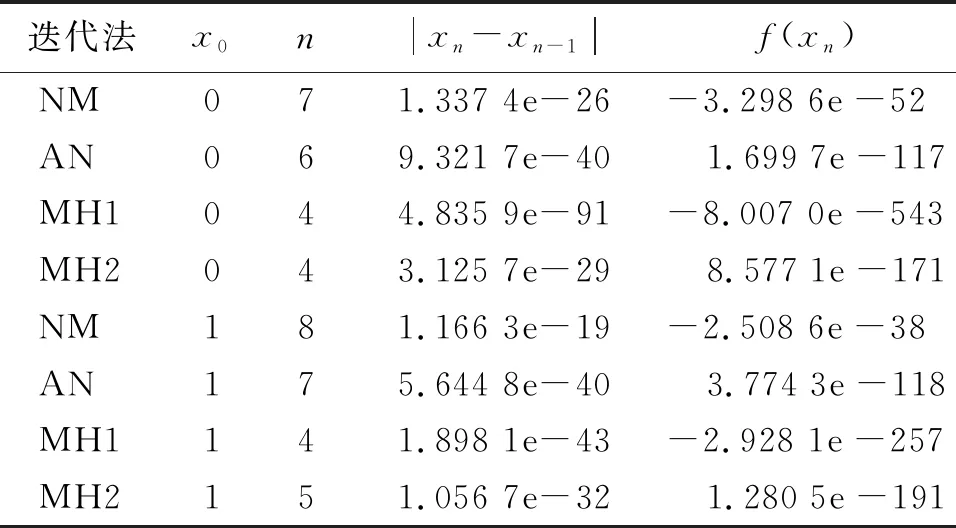
表4 测试函数为f4(x)的数值实验Tab.4 Numerical experimental results of test function f4(x)

由表中数据可以看出，迭代法(1)和(2)的迭代次数均少于牛顿迭代法和算术平均牛顿法，这也印证了迭代法(1)和(2)的收敛阶要高于牛顿迭代法和算术平均牛顿法.此外，表2显示，当迭代初值为1时，迭代法(1)的迭代次数比迭代法(2)少1次.而表4结果也显示，当迭代初值为1时，出现了同样的结果.可见在有些情况下，迭代法(1)的收敛速度比迭代法(2)更快.

4 结论

数值实验结果表明，两种六阶收敛的迭代法具有更快的收敛速度，并且在提高收敛速度的同时，仅增加了很小的计算成本，具有一定的优越性.迭代法(1)是在牛顿迭代法的基础上，每一步迭代增加了一个函数值、一个导数值和一个二阶导数值的计算，效率指数从之前的1.414增加到了1.431.迭代法(2)是在算术平均牛顿法的基础上，每一步迭代增加了一个函数值的计算，效率指数从之前的1.442增加到了1.565.可见新的迭代法对于理论和实际应用都具有一定的意义.