凃 强 程 琳 孙 超 唐 芳 李嫚嫚

(1东南大学交通学院, 南京 210096)(2江苏大学汽车与交通工程学院, 镇江 212013)

不确定环境下的交通网络建模一直是交通领域的研究热点,受到出行需求和道路通行能力变化的影响,起讫点(origin-destination,O-D)之间的路径出行时间也会在一定范围内波动[1].面对随机交通网络,出行者表现出风险规避行为,不仅关注出行时间的期望值,同时也关注出行时间的可靠性[2],在此基础上主要有2类路径选择行为:① 一定可靠度下,选择出行时间预算最小的路径[3-4];② 一定出行时间预算下,选择准时到达概率最高的路径[5-6].相应的交通分配模型主要关注第①类路径选择行为,包括出行时间预算(travel time budget,TTB)模型、均值-超额出行时间(mean-excess travel time,METT)模型、迟到惩罚用户均衡(late arrive penalty user equilibrium,LAPUE)模型等[7-9];针对第②类路径选择行为的交通分配模型较少,仅有Sun等[10]提出的基于可靠性的有限理性用户均衡模型,但并没有考虑随机出行时间的有界性.

现有模型大多使用中心极限定理估计路径出行时间分布,其假设路段出行时间相互独立,从而路径出行时间近似服从正态分布.但是根据正态分布的特征,出行时间有小概率出现负值或者无穷大的极端情况,忽略了路径随机出行时间的有界性,与现实情况不符.关注随机出行时间的有界性,姚志洪等[11]采用实测和仿真数据,对出行时间的不确定性进行估计,发现截断正态分布具有很好的拟合效果;Xu等[12]考虑路段限速,以限速下的路段出行时间为下界,将截断随机出行时间分布应用到了METT模型中,分析了路段限速对不确定环境下交通网络的影响;在此基础上,Zhao等[13]将自由流出行时间作为下界,建立了一个TTB-SUE(travel time budget based stochastic user equilibrium)模型.综上,现有交通分配模型对于出行时间的有界性考虑较少,且仅考虑了出行时间下界对于交通网络流量分布的影响,同时忽略了对第②类路径出行选择行为的影响.

对于通勤出行者而言,出发时刻确定的条件下,更加关注在出行时间预算内准时到达目的地的概率,以避免迟到带来的惩罚,这种情况下第②类路径出行选择行为更具有现实意义.而出行时间分布的上界可以视作交通网络面对不确定情况的可靠性,一定程度上反映了交通管理和控制水平,比如地铁等轨道交通相比地面小汽车交通具有更高的可靠性.基于此,本文将同时考虑这2个要素,建立截断随机出行时间下的可靠网络均衡模型,并对比分析出行时间上界对于网络流量分布和准时到达概率的影响.

1 问题描述与网络建模

1.1 截断随机出行时间

考虑随机交通网络G(N,A),其中,N为节点集合,A为路段集合,路段出行时间Ta采用BPR函数表示,即

(1)

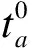
(2)

(3)

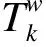
(4)

(5)

式中,δa,k为路段路径关联系数,当路径k经过路段a时,δa,k=1,否则δa,k=0.

采用正态分布描述路径出行时间的明显缺陷在于出行时间可能出现较小(甚至负值)和无穷大的情况,考虑到路径出行时间的有界性,采用截断正态分布描述出行时间分布更加符合真实情况,其概率密度函数可表示为

(6)

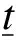
(7)

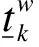
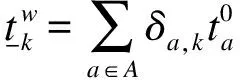
(8)

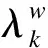
1.2 准时到达概率

对于通勤出行者而言,制定完成出行时间预算后,会选择准时到达概率更高的路径以避免迟到惩罚.出行时间预算定义为最小路径期望出行时间和缓冲时间之和,其表达式如下:

(9)

式中,bw为O-D对w的出行时间预算;ε为缓冲时间,表示期望出行时间之外的预留时间,以避免期望之外的延误而造成迟到.

(10)

式中,Pr{B}为事件B的概率.

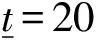
1.3 可靠网络均衡模型

在随机交通网络中,给定出行时间预算下,每个出行者都试图选择准时到达概率最大的路径,交通网络将达到这样一个均衡状态:同一O-D对中所有使用路径的准时到达概率相等且最大,不小于所有未使用路径的准时到达概率,任何出行者都不可以通过单方面调整路径提高准时到达概率,即

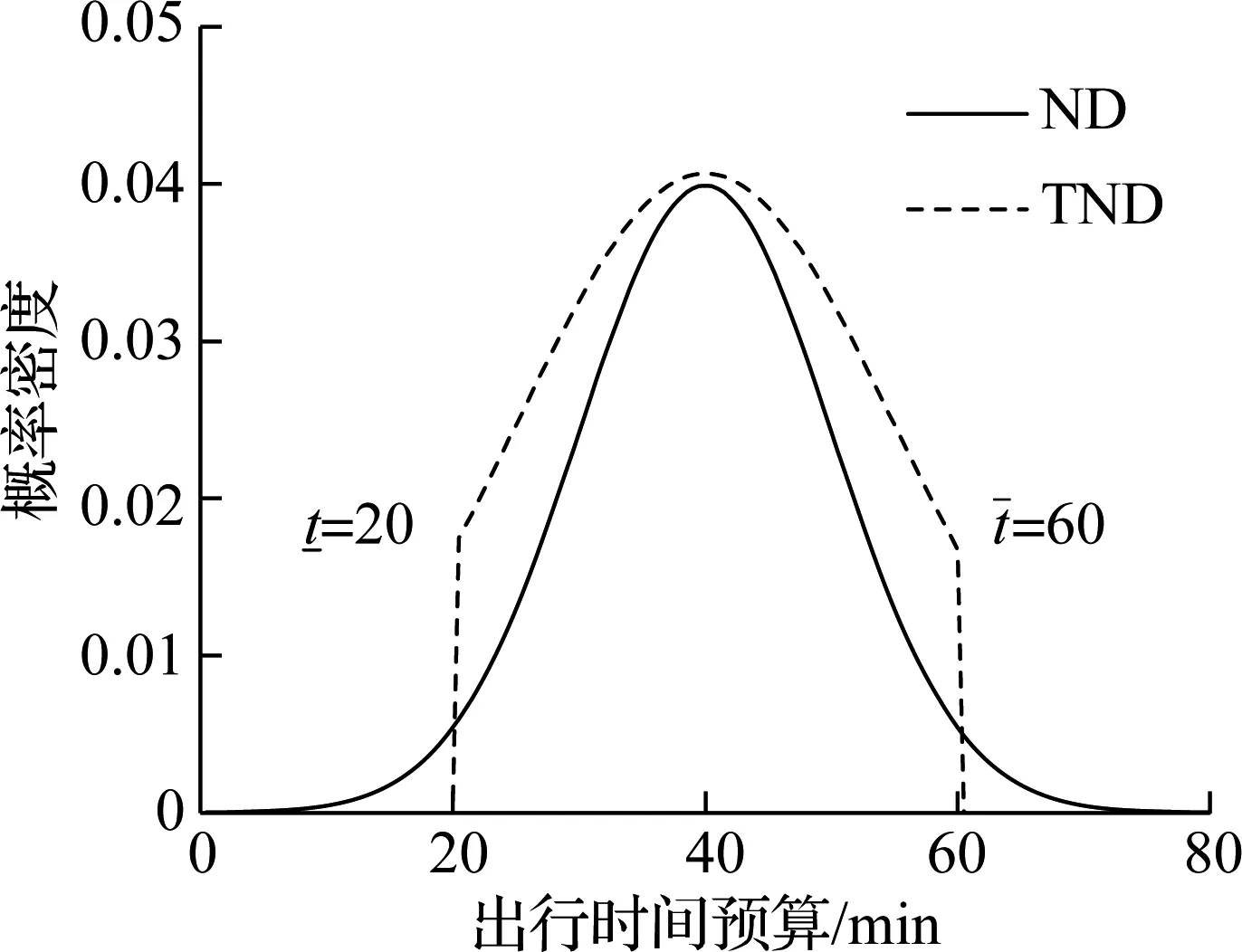
(a) 概率密度分布

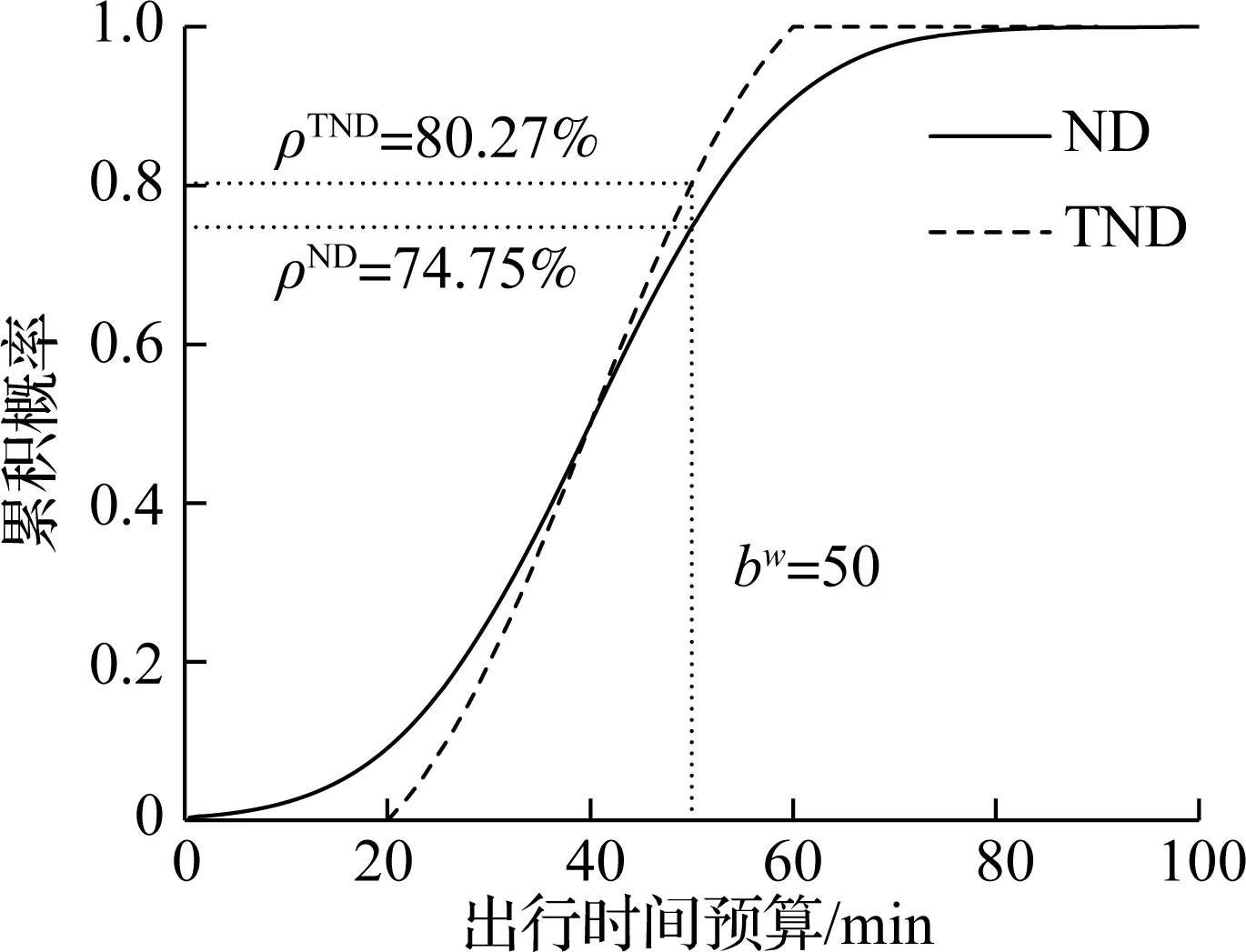
(b) 累积概率分布

(11)

令h∈Ω={Δh=q,h≥0,q≥0},其中,h为路径流量向量,Ω为可行域,q为交通需求向量,Δ为路径流量和交通需求关系矩阵,则均衡条件可以等价表示为如下的变分不等式模型:

〈ρT,(h*-h)〉≥0

(12)

式中,h*为均衡状态下的路径流量向量;ρ为路径准时到达概率向量.

式(12)等价于ρTh≤ρTh*,因此,h*是变分不等式模型式(12)的解,当且仅当h*是如下线性规划问题的解:

(13)

进一步考虑上述线性规划问题标量形式的拉格朗日函数,即

(14)

式中,W为O-D对集合;Kw为O-D对w间的路径集合;qw为O-D对w间的交通需求.

由此可以得到上述线性规划问题的Karush-Kuhn-Tucker(KKT)条件为

(15)

显然式(15)等价于均衡条件式(11)，由此证明了变分不等式模型式(12)等价于均衡条件式(11).

2 求解算法

网络均衡问题的求解方法包括基于路段和基于路径的算法.基于路段的求解算法中,每次迭代都需要对网络中的每个O-D求解一次最短路径问题,由于随机网络中可靠最短路径求解过程较为复杂且耗时较长(尤其在大规模网络中)[14],因此,基于路段的求解算法实现较为困难,其应用也较少.目前,求解随机网络中的均衡问题主要采用基于路径的方法,其主要思想是预先生成一个工作路径集合,每次迭代过程中只需要比较O-D间路径集合中所有路径的目标函数值(如本文为准时到达概率),然后选出最优路径,从而简化了最短路径的求解过程[15],大大缩减了均衡问题的求解时间.工作路径集合的生成大多采用Bekhor等[16]提出的方法.此外,随着数据检测技术的发展,基于GPS等高精定位技术的车辆轨迹识别也为O-D间的工作路径集合生成提供了新的思路[17].

MSA算法是一类求解网络均衡问题的通用迭代算法框架,具有很好的收敛特性[18].结合前文所述,本文采用基于路径的MSA算法求解网络均衡问题,其步骤如下：

① 初始化.计算零流量下,路径初始准时到达概率ρ,对交通需求q在路网上进行全有全无分配,得到初始路径流量h(0),设置迭代次数m=0.

② 更新路径准时到达概率.根据路径和路段流量关系,计算第m次迭代的路段流量x(m),按照式(2)～(10)更新路径准时到达概率ρ.

③ 确定方向.根据更新的路径准时到达概率,进行全有全无分配,得到第m次迭代的辅助路径流量h(m)′.

④ 更新路径流量.计算第m+1次迭代的路径流量h(m+1)=h(m)+λ(m)(h(m)′-h(m)),其中λ(m)为步长,λ(m)=1/m.

⑤收敛判断.若‖h(m+1)-h(m)‖/‖h(m)‖≤e,e为预定义的收敛精度，算法终止,h(m+1)为最优解;否则令m=m+1,转至步骤②.

3 算例分析

表1 Nguyen-Dupuis网络路段数据

首先对算法的收敛性和结果的有效性进行分析.如图3所示,在运算时间0.15 s左右算法的整体精度达到了10-3,在1 s左右精度达到10-4左右.

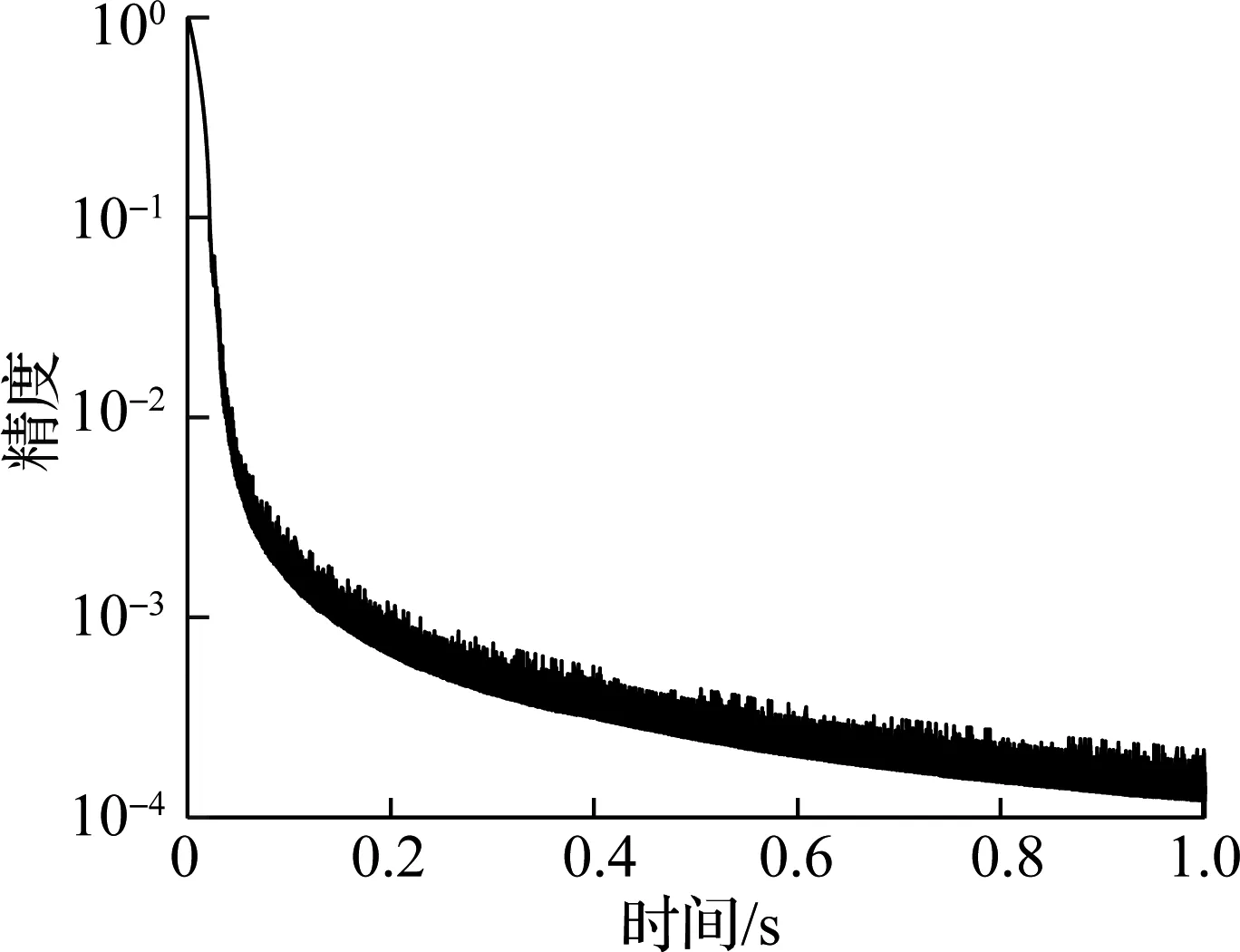
(a) 整体精度收敛速度

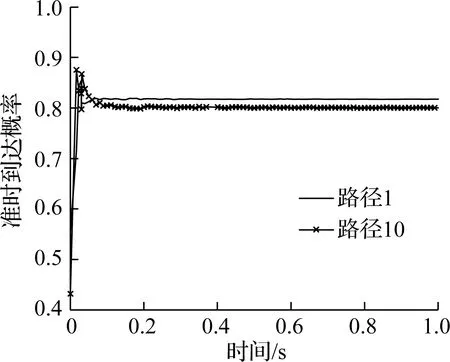
(b) 路径准时到达概率收敛速度

以路径1和路径10(路径编号见表2)为例,分析路径准时到达概率收敛情况,可知在0.3 s左右均能收敛到最优解附近,表明算法能够在短时间内收敛到较高的精度.如表2所示,不管是在ND和TND下,计算结果均满足可靠网络均衡状态的定义,即所有使用路径的准时到达概率都是最大且相等的,说明了可靠网络均衡模型和MSA算法的有效性.

以O-D对1-3和4-2为例,表2对比了ND和TND下模型的路径数据结果.对比发现,2个模型的路径数据结果存在较大差异:考虑随机出行时间的有界性时,O-D对1-3的OTAP由0.752上升到0.817,同时使用路径由4条变为3条;O-D对4-2的OTAP由0.762上升到0.800,同时使用路径由3条变为4条,相应地路径流量分布也发生了变化.

除了路径数据结果的变化,路段流量分布的变化情况同样值得关注.令ND和TND下路段流量分别为xa,ND和xa,TND,则路段a的流量相对变化值

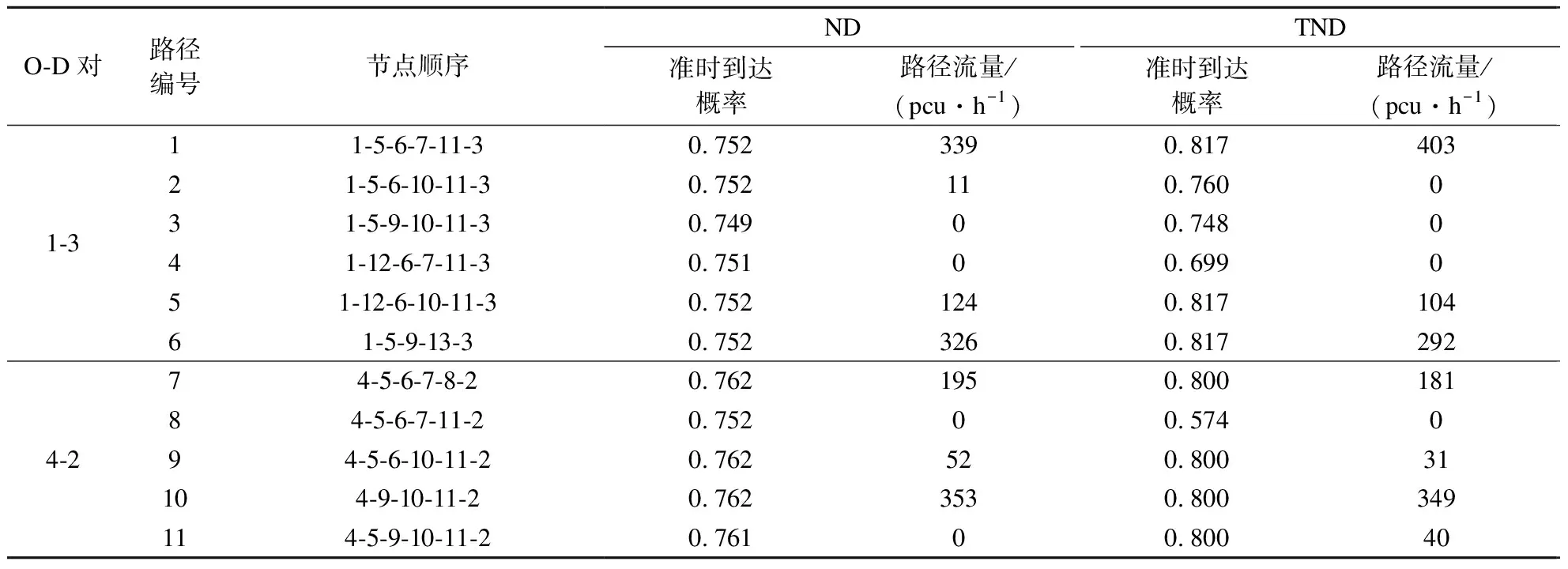
表2 ND和TND下模型的路径数据结果对比

Ra的计算方法为

(16)

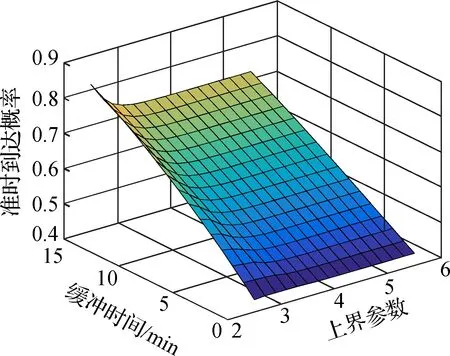
图4展示了在ND和TND下19条路段的流量分布的绝对值和相对变化值.由图可知,不同分布假设下,路段流量分布产生了较大的变化,其中路段8流量的绝对值和相对变化值均增长最多,分别为52.1和38.5%;路段10流量的绝对值和相对变化值均减少最多,分别为63.8和15.8%;路段18流量的绝对变化值和相对变化值最小,均接近于零.缓冲时间代表了出行者面对不确定性的风险规避水平[8],其取值越大,说明出行者风险规避水平越高;而随机出行时间的上界一定程度上反映了交通管理控制水平,下面对2个参数进行敏感性分析.图5展示了O-D对1-3和4-2的准时到达概率随缓冲时间ε和上界参数λ的变化情况的曲面图,可知随着缓冲时间的增加和上界参数的降低,O-D间的准时到达概率将增加.

图6则展示了准时到达概率的变化曲线图.首先固定ε=10,上界参数λ由2变为4,随着λ变大,O-D间的准时到达概率逐渐趋于稳定,这是由于当λ增加到一定程度,出行时间上界的正态分布累积概率都很接近于1,由式(7)可知,准时到达概率将趋于稳定,其结果约等于不考虑随机出行时间上界的情况;然后固定λ=2,缓冲时间ε由零变到15 min,随着ε变大,O-D间的准时到达概率都将趋于1,并最终等于1,比如当ε=15 min时O-D对1-2的准时到达概率等于1,而在正态分布随机出行时间下,准时到达概率只能无限接近于1.

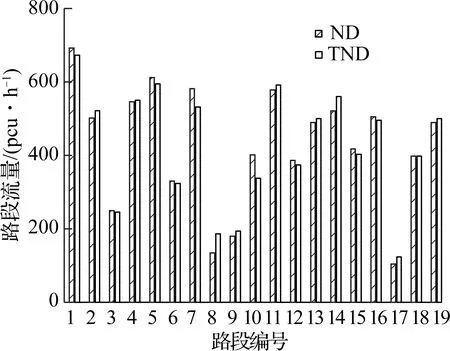
(a) 路段流量绝对值

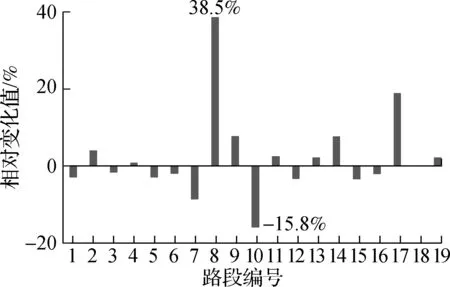
(b) 路段流量相对变化值

(a) O-D对1-3

(b) O-D对4-2

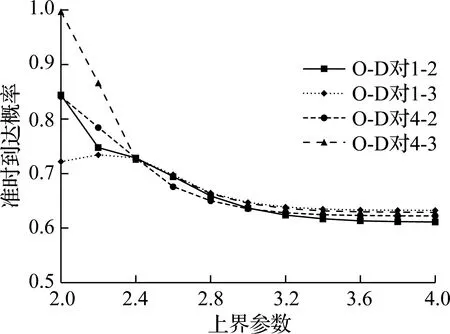
(a) 准时到达概率随上界参数变化情况

(b) 准时到达概率随缓冲时间变化情况

4 结论

1) 考虑了随机出行时间分布的有界性,采用截断正态分布来描述路径出行时间,分析了路径准时到达概率的变化情况.

2) 基于准时到达概率建立了可靠网络均衡模型,同时建立了等价的变分不等式模型,分析了解的存在性,采用MSA算法对模型进行求解.

3) 在Nguyen-Dupuis网络中验证了可靠网络均衡模型和MSA算法的有效性,ND和TND下的模型结果存在较大差异,其中最大路段流量相对变化值达到38.5%.提高缓冲时间或者降低出行时间上界均可有效提升O-D间的OTAP,并最终趋于1.

4) 本文进一步可拓展的研究方向有:交通需求不确定下的可靠网络均衡模型,多交通模式下的可靠网络均衡模型,考虑出行者异质性的可靠网络均衡模型,日变动态交通网络演化模型,以及交通网络设计问题等.