张 迪，成央金，杨 柳

湘潭大学 数学与计算科学学院,湖南 湘潭411105

1 引言

自从1965年，Zadeh[1]提出了模糊集的概念之后，引起了众多学者的广泛关注。模糊集理论也被当作一种处理模糊性和不确定性信息的有效工具应用到各个领域。在实际的决策问题中，由于决策者在给出评价信息时，会受到客观环境和专业水平等因素的影响，使得作出决策时犹豫不决，并且不同决策者所给出的评价值有所不同。Torra[2]提出了犹豫模糊集的概念，它允许有多个元素对集合的隶属度。由于决策者有时候不能给出确切的评价信息值，于是文献[3]提出了区间犹豫模糊集。随后，戴意瑜等人[4]基于三角模糊数和犹豫模糊数提出了三角犹豫Einstein算法的多属性决策模型。周晓辉等人[5]基于区间直觉梯形模糊数提出了区间直觉梯形模糊几何Heronian平均算子，并将其应用到模糊多属性决策中。

而在模糊多属性决策的问题中，信息集成算子也是一个重要的研究部分。Yager 等人[6]定义了有序加权平均（OWA）算子，随后，又有人定义了有序加权几何平均（OWGA）算子、有序加权调和平均（OWHA）算子。犹豫模糊集概念提出以后，Zhou 等人[7]提出了犹豫模糊Hamacher加权平均（HFHWA）算子、犹豫模糊Hamacher有序加权平均（HFHOWA）算子和犹豫模糊Hamacher混合平均（HFHHA）算子等。然而在现实的决策问题中，输入变量之间或多或少会有相互影响。Yager 等人[8]提出了广义Bonferroni Mean（BM）算子，能够很好地反映这种输入变量之间的关系。随后，Zhu 等人[9]又提出了犹豫模糊Bonferroni Mean（HFBM）算子，犹豫模糊几何Bonferroni Mean（HFGBM）算子；针对属性值的重要程度不同，提出了犹豫模糊加权Bonferroni Mean（HFWBM）算子和犹豫模糊加权几何Bonferroni Mean（HFWGBM）算子。朱轮等人[10]提出了广义犹豫模糊Bonferroni 平均算子，并将其应用到多准则群决策中。于倩等人[11]提出了区间犹豫模糊Bonferroni Mean（IVHFBM）算子、区间犹豫模糊几何Bonferroni Mean算子、区间犹豫模糊加权Bonferroni Mean（IVHFGBM）算子、区间犹豫模糊加权几何Bonferroni Mean（IVHFWGBM）算子，并将其在多属性决策中的应用。由于所给出的评价信息和属性权重会存在模糊性和不确定性，2018年于倩等人[12]提出了犹豫梯形模糊加权平均（HTrFWA）算子和犹豫梯形模糊加权几何（HTrFWG）算子，并将其应用到多属性决策中去。

目前，基于Bonferroni Mean（BM）算子的区间犹豫梯形模糊环境下的多属性决策方法的研究还没有。于是基于Chen等人[13]的区间梯形模糊数和犹豫模糊集提出了区间犹豫梯形模糊Bonferroni Mean（IVHTrFBM）算子和区间犹豫梯形模糊几何Bonferroni Mean（IVHTrFGBM）算子。结合犹豫模糊元的运算法则给出了区间犹豫梯形模糊元的运算法则，并够构造了的得分函数进行排序；又根据输入变量的重要程度不同，提出了区间犹豫梯形模糊加权Bonferroni Mean（IVHTrFWBM）算子和区间犹豫梯形模糊加权几何Bonferroni Mean（IVHTrFWBM）算子。最后，又针对评价信息为区间犹豫梯形模糊集的多属性决策问题提出了基于IVHTrFWBM算子和IVHTrFWGBM 算子的多属性决策方法，并用算例证明了该方法的可行性和有效性。

2 预备知识

2.1 区间犹豫梯形模糊集

定义1 设X 是一非空集合，则集合

称为区间犹豫梯形模糊集（IVHTrFSs），其中hA(x)是由[0,1]上所有不同区间梯形模糊数构成的。hA(x)是表示x ∈X 隶属于A 的所有不同隶属度的集合。

其中，0 ≤aL≤bL≤cL≤dL≤1,0 ≤aU≤bU≤cU≤dU≤1以及aL≤aU,bL≤bU,cL≤cU,dL≤dU。特别地，当aL=aU,bL=bU,cL=cU,dL=dU时，hA(x)就退化成犹豫梯形模糊元（HTrFE）。

定义2[3]区间犹豫梯形模糊元的运算法则：

定义3[3]设h 是一个区间犹豫梯形模糊元，h={γ|γ ∈h}，则称为h 的得分函数。其中lh是h 中的区间梯形模糊数的个数，s(h)是区间[0,1]的区间梯形模糊数。对于两个区间犹豫梯形模糊元h1和h2，如果s(h1)＞s(h2) ，则h1＞h2；如果s(h1)=s(h2) ，则h1=h2。对于h1和h2的大小可用上述方法进行比较。

定义4[14]设a=[aL,aU],b=[bL,bU] 为两个区间数，且λ ≥0，则它们满足以下性质：

2.2 BM算子

定义5[15]设p,q ≥0,ai≥0(i=1,2,…,n)为实数集，若存在称函数Bp,q为BM算子。

容易证明BM算子满足以下性质。

性质1（幂等性）设ai为非负实数集，如果有ai=a(i=1,2,…,n)，则有：

性质2（有界性）设ai为非负实数集，如果有a-=min(ai),a+=max(ai)，则有：

性质3（单调性）设ai(i=1,2,…,n),bi(i=1,2,…,n)为非负实数集，如果存在∀i，且ai≤bi，则有：

性质4（置换不变性）设ai,a′i为非负实数集，其中(a′1,a′2,…,a′n)为(a1,a2,…,an)的任意置换，则有：

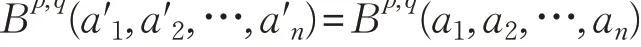
针对参数p、q 的取值不同，进一步探讨BM集成算子的一些特例：

（1）当p=1,q=1时，Bp,q(a1,a2,…,an)=B1,1(a1,a2,…,

（2）当q=0时，Bp,q(a1,a2,…,an)=Bp,0(a1,a2,…,an)=

（3）当p=1,q=0时，Bp,q(a1,a2,…,an)=B1,0(a1,a2,…,

2.3 GBM算子

定义6[9]设p,q ≥0,ai≥0(i=1,2,…,n) 为实数集，若存在：称函数GBp,q为几何Bonferroni Mean（GBM）算子。

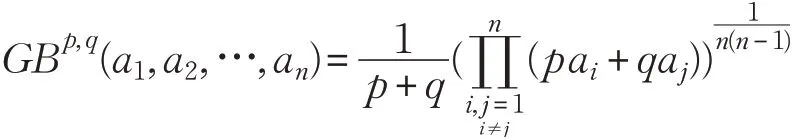
容易证明GBM 算子与BM 算子有类似的性质，篇幅有限在这里不一一赘述。

2.4 IVHTrFBM算子和IVHTrFWBM算子

2.4.1 IVHTrFBM算子

定义7 设hi(i=1,2,…,n)为区间犹豫梯形模糊元，对于p,q ≥0，若存在：称函数IVHTrFBp,q为区间犹豫梯形模糊Bonferroni Mean（IVHTrFBM）算子。

定理2 设hi(i=1,2,…,n)为区间犹豫梯形模糊元，对于p,q ≥0，使用IVHTrFBM 算子集成后的结果仍是区间犹豫梯形模糊元，且：

容易证明，IVHTrFBM 集成算子和BM 算子有类似的性质，如下：

下面是IVHTrFBM集成算子的一些特例。

（1）当q →0 时，有：

（2）当p=2,q →0 时，有：

（3）当p=1,q →0 时，有：

（4）当p=1,q=1 时，有：

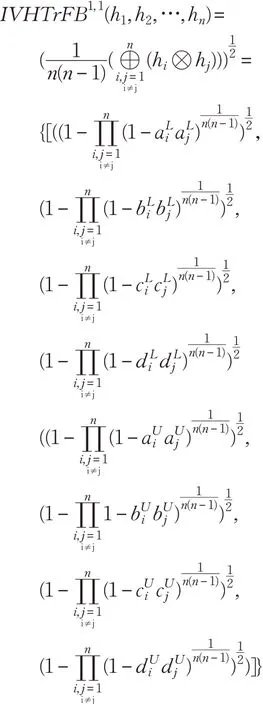
2.4.2 IVHTrFWBM算子

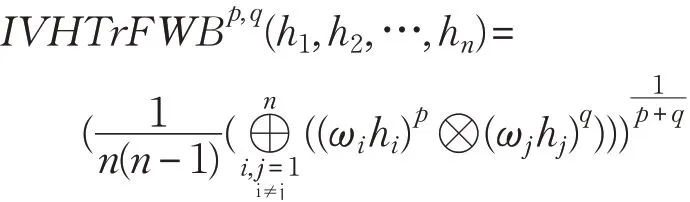
称函数IVHTrFWBp,q为区间犹豫梯形模糊加权Bonferroni Mean(IVHTrFWBM)算子。

2.5 IVHTrFGBM算子和IVHTrFWGBM算子

2.5.1 IVHTrFGBM算子

定义9 设hi(i=1,2,…,n)为区间犹豫梯形模糊元，对于任意的p,q ≥0，若存在：

称函数IVHTrFGBp,q为区间犹豫梯形模糊几何Bonferroni Mean(IVHTrFGBM)算子。

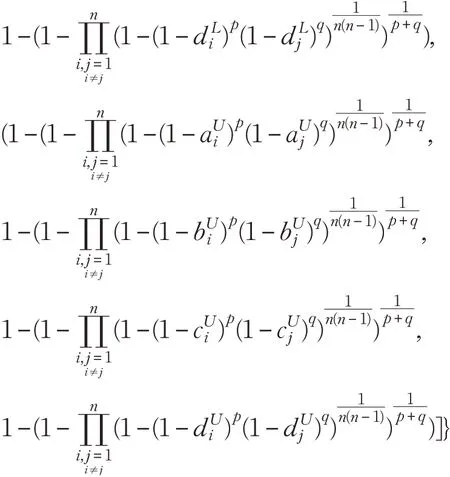
下面是IVHTrFGBM算子的相关性质：

下面是IVHTrFGBM集成算子的一些特例。

（1）当q →0 时，有：

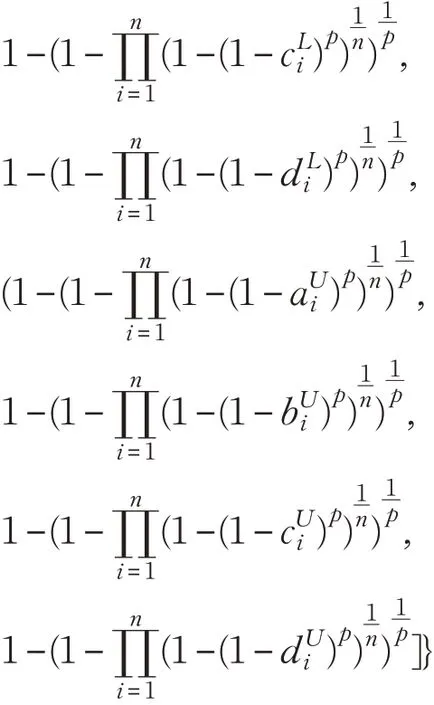
（2）当p=2,q →0 时，有：

（3）当p=1,q →0 时，有，

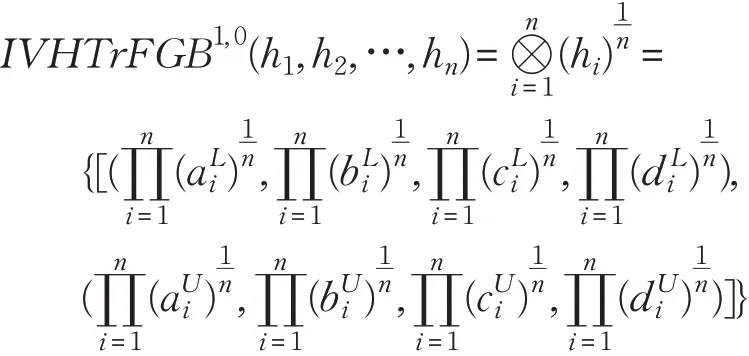
（4）当p=1,q=1 时，有：

称函数IVHTrFWGBp,q为区间犹豫梯形模糊加权几何Bonferroni mean（IVHTrFWGBM）算子。

3 基于IVHTrFWBM 算子和IVHTrFWGBM算子的多属性决策方法

对于某个多属性决策问题，方案集为A={A1,A2,…,An}{i=1,2,…,m}，属性集为C={C1,C2,…,Cn}{j=1,2,…,n},ω=(ω1,ω2,…,ωn)T为专家给出的属性集C 的权重向量，表示属性不同重要程度且。专家经常给出不同的备选方案Ai，相对于属性Cj的区间评价值用区间犹豫梯形模糊变量表示，从而构成区间犹豫梯形模糊矩阵H=(hij)m×n。

3.1 IVHTrFWBM 算 子 和IVHTrFWGBM 算子的算法步骤

步骤1.1 利用给定的区间犹豫梯形模糊矩阵和IVHTrFWBM算子计算Ai的综合区间犹豫梯形模糊评价值hi(i=1,2,…,m)：

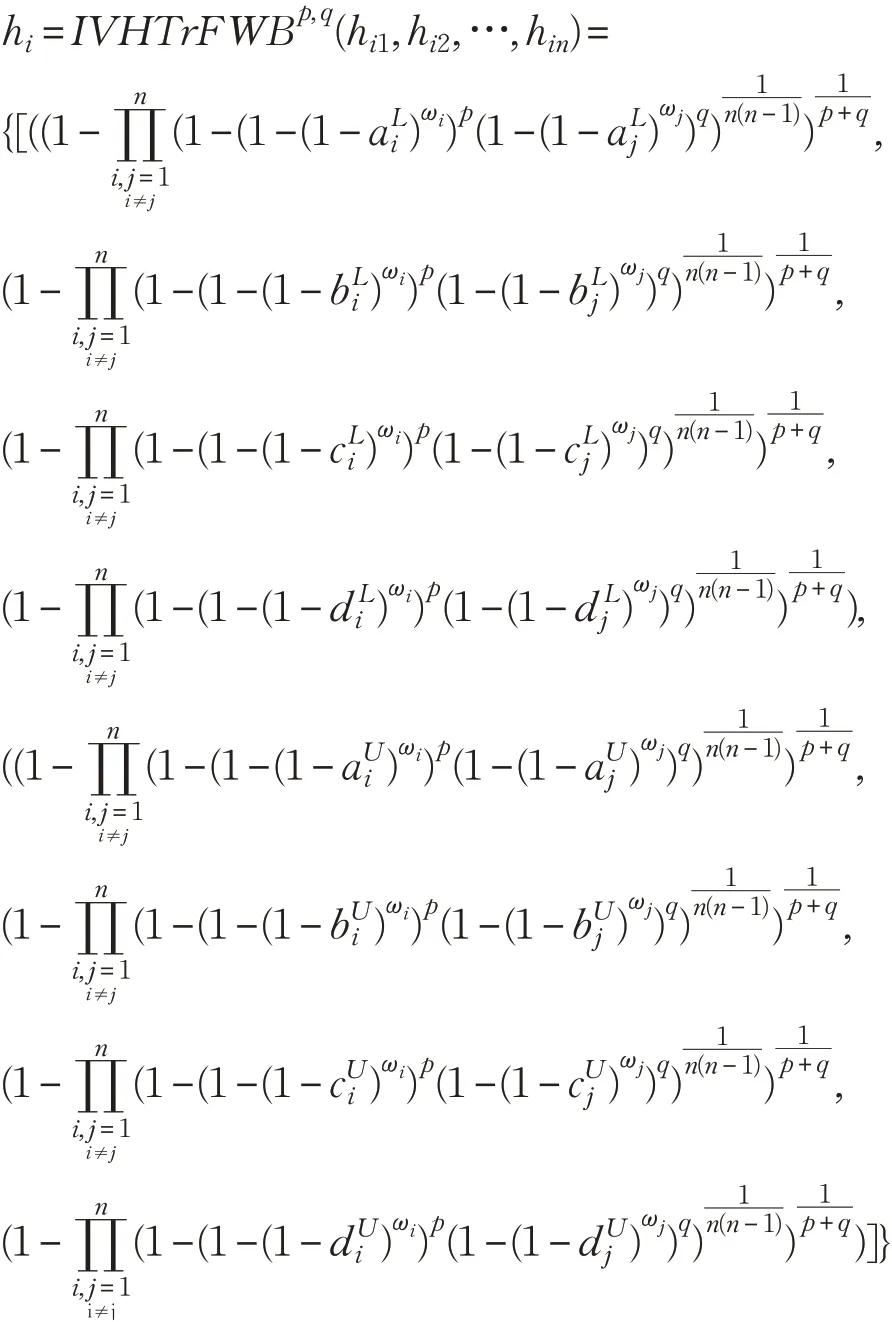
步骤1.2 利用给定的区间犹豫梯形模糊矩阵和IVHTrFWGBM 算子计算Ai的综合区间犹豫梯形模糊评价值hi(i=1,2,…,m)：

步骤2 计算hi的得分函数s(hi)(i=1,2,…,m)。

步骤3 对s(hi)进行排序。

步骤4 根据s(hi) 的排序大小，选择相应的最优方案。

3.2 算例分析

对于一个生产型企业选择绿色供应商问题，假设现有5 个绿色供应商Ai{i=1,2,3,4,5}，分别从如下4 个属性Cj{j=1,2,3,4}去评价：C1产品竞争力；C2合作与发展潜力；C3供应商竞争力；C3绿色绩效。ω=(0.2,0.1,0.3,0.4)T是权重向量。专家给出各个备选绿色供应商在上述4 个属性下的评价值以区间犹豫梯形模糊集的形式表示，各个属性评价构成区间犹豫梯形模糊决策矩阵H=(hij)5×4如表1所示。

为了选择出最优的绿色供应商，下面是具体算法实现步骤：

步骤1.1 为了不失一般性，参数p、q 选择如下3种情形：（1）p=1,q=1；（2）p=1,q=2；（3）p=2,q=2。利用给定的区间犹豫梯形模糊矩阵和IVHTrFWBM 算子，对各方案进行集结。下面是以p=1,q=1 为例计算Ai的综合区间犹豫梯形模糊评价值hi(i=1,2,…,m)。由于篇幅有限，其他不同参数的各方案综合区间犹豫梯形模糊评价值，在这里不一一赘述。

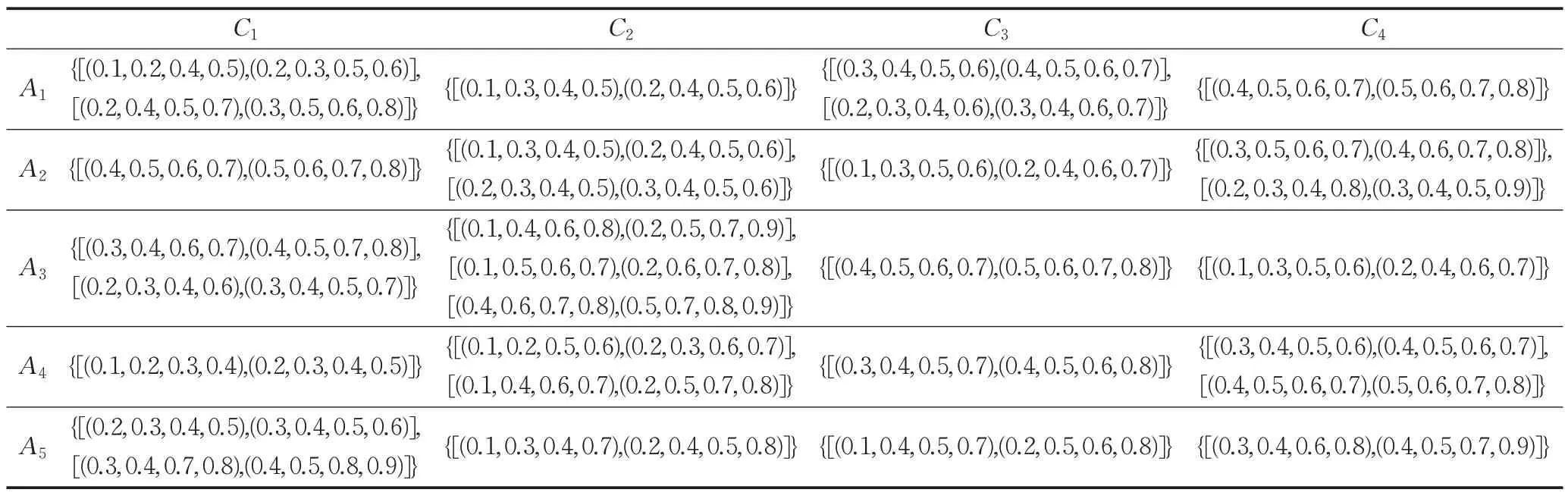
表1 区间犹豫梯形模糊决策矩阵

得到方案Ai的综合区间犹豫梯形模糊评价值hi(i=1,2,3,4,5)：

步骤1.2 为了不失一般性，参数p、q 选择如下3种情形：（1）p=1,q=1；（2）p=1,q=2；（3）p=2,q=2。利用给定的区间犹豫梯形模糊矩阵和IVHTrFWGBM 算子，对各方案进行集结。下面是以p=1,q=1 为例计算Ai的综合区间犹豫梯形模糊评价值hi(i=1,2,…,m)。由于篇幅有限，其他不同参数的各方案综合区间犹豫梯形模糊评价值，在这里不一一赘述。

得到方案Ai的综合区间犹豫梯形模糊评价值hi(i=1,2,3,4,5)：

步骤2 计算不同参数下各方案综合区间犹豫梯形模糊评价值hi的得分函数s(hi)(i=1,2,3,4,5)如表2和表3所示。

步骤3 对得分数值s(hi)进行排序如表4所示。

步骤4 根据s(h1)的排序大小，选择相应的最优案。

分析可知，对参数p、q 赋予不同的数值，两种算子对各供应商的排序结果有略微不同，但最终决策结果相同；且绿色供应链中最优供应商是A5。

4 结束语

基于犹豫梯形模糊集和区间梯形模糊集，首先定义了区间犹豫梯形模糊集以及它的运算法则。又在此基础上探讨了区间犹豫梯形模糊Bonferroni Mean算子和区间犹豫梯形模糊几何Bonferroni Mean 算子；考虑到专家给出评价值的重要程度不同，又进一步讨论了区间犹豫梯形模糊加权Bonferroni Mean算子和区间犹豫梯形模糊加权几何Bonferroni Mean 算子。最后，基于区间犹豫梯形模糊加权Bonferroni Mean算子和区间犹豫梯形模糊加权几何Bonferroni Mean算子的多属性决策方法，并通过算例证明其有效性和可行性。

表2 各方案得分值（IVHTrFWBM）

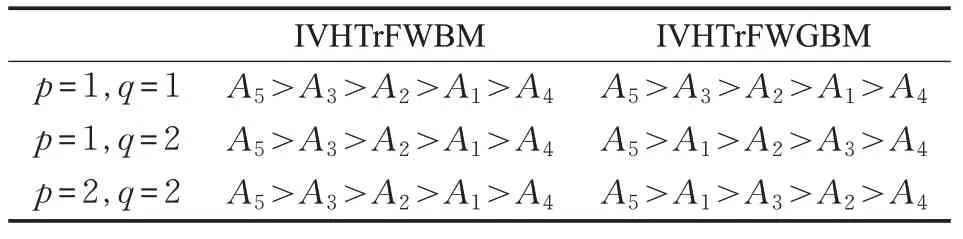
表4 排序结果

今后的工作中，仍需研究解决的问题：文中随着参数p、q 取值不同，得到的最终排序结果不稳定。有多个专家评价的区间犹豫梯形模糊多属性决策问题。