一维Marchenko自聚焦算法的数值解与解析解∗
2019-11-30胥利文张秀梅王秀明
胥利文 陈 浩 张秀梅 王秀明
(1 中国科学院声学研究所 北京 100190)
(2 中国科学院大学 北京 100049)
(3 北京市海洋深部钻探测量工程技术中心 北京 100190)
0 引言
波动方程逆散射问题的研究是声波在固体介质中传播和成像理论的重要研究内容。一维波动方程逆散射问题的经典解之一就是Marchenko 方程[1],它将介质边界上单边记录的波场响应和来自于介质内部声源的散射响应通过积分耦合,可以用来反演介质内部的构造。最近,Broggini 等[2]展示了在不需要知道介质信息的情况下,利用单边记录的反射响应重构介质中虚拟点源的格林函数。Wapenaar 等[3]通过引入波场的因果性条件,将上述方法推广到多维介质中。van der Neut等[4]提出多维互相关理论,解释了如何通过波场迭代求解多维Marchenko方程。Cui 等[5]将方程求解过程中定义的聚焦函数解释为边界源在负时刻的入射波场,分析了基于初始聚焦函数求取单程格林函数过程中幅度对结果的影响。除应用在弹性介质中,Marchenko自聚焦方法还可用于复杂的黏弹性介质成像中[6−7]。
本文主要研究在一维介质中,介质表面到介质内任一点之间的格林场是如何通过耦合Marchenko方程组求解得到的,首先解释了如何利用单程波场的互易原理推导耦合Marchenko 方程组;接着基于波场的因果性,设计时间窗算子迭代求解聚焦函数,并利用聚焦函数求解期望的格林函数;然后在求解过程中引入卷积理论,分别在数值解和解析解模型中计算期望的格林函数;最后基于解析解分析数值解中各个波形序列构造的具体过程。
1 Marchenko方程
本文将声学介质限制在一维状态,模型如图1所示,蓝实线表示声速,红虚线表示密度,位于介质表面的黑色五角星和倒三角形分别表示声源和接收器,在深度z=900 m 处的红色五角星表示介质中的虚拟点源,也是下文所述的聚焦函数的聚焦点。其中图1(a)为状态B,代表实际介质;图1(b)为状态A,表示参考介质。两种介质的不同之处在于参考介质中用红色五角星表示的声源下方是均匀介质,声波入射之后无反射,相当于实际介质的截断版本。在两种状态下,对于两个在时间轴上正向传播的波场,可以通过卷积型互易原理联系[8]:
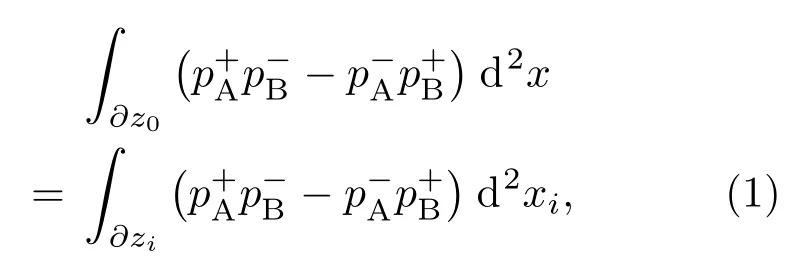
对于时间轴上正向传播的波场和反向传播的波场,通过相关型互易原理联系[8]:
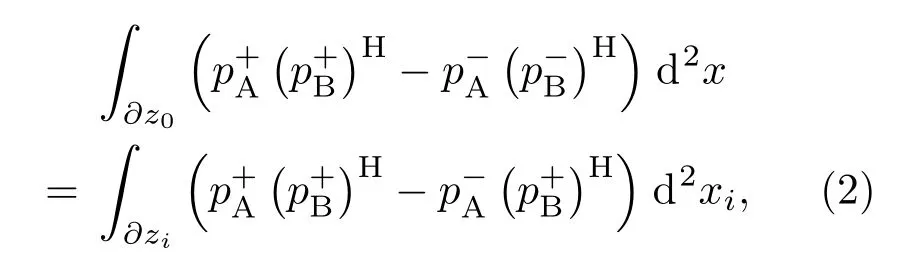
式(1)~(2)中,pA和pB分别是两种介质中记录的波场,“+”表示声波朝深度增加的方向传播,“−”表示声波朝深度减小的方向传播,本文分别用它们表示下行和上行的单程波场,()H为复共轭。等式(1)和等式(2)的左边积分区域是沿着介质表面∂z0(z= 0 m)积分,右边是沿着定义的聚焦平面∂zi(z=900 m)积分。
在状态A 中的介质表面上方,如果布置一个向深度方向发射声波的脉冲点声源,则介质表面记录的下行波场为p+A=δ(x −x0),其中x0是声源的水平坐标位置,在本文所示的一维介质中x0= 0,因此p+A=δ(x)。同时介质表面也会记录来自于介质内部的反射响应,即上行波场p−A=RA(z0,z0,t)。在定义的聚焦点z=900 m处记录的下行波场是参考介质的透射响应p+A=TA(zs,z0,t),同时因为在聚焦点下方是均匀介质,无反射波,因此聚焦点处记录的上行波场为0,即p−A=0。
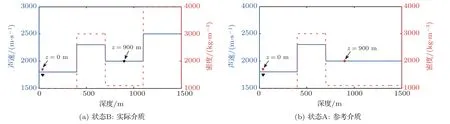
图1 1D 数值解模型Fig.1 1D numerical model
同理,在状态B 中的介质表面上方,也布置一个向深度方向发射声波的点声源,则介质表面记录的下行波场为p+B=δ(x),上行波场是实际介质的反射响应,即p−B=R(z0,z0,t)。在聚焦点处,可以将记录的全波场G(zs,z0,t),分解为上行波场p−B=G−(zs,z0,t)和下行波场p+B=G+(zs,z0,t),即G=G++G−。上述两种状态中的表达式R(z0,z0,t)、T(zs,z0,t)和G(zs,z0,t),括号中的第一项表示接收器,第二项表示声源,都表示声源发射、接收器接收的波场响应。
状态A 中参考介质的透射响应TA(zs,z0,t)和反射响应RA(z0,z0,t)是未知的,在状态A 中定义一种新的函数:聚焦函数f1(z0,zs,t),它的下行分量f1+(z0,zs,t)被定义为透射响应的时反,表示从介质表面z0发射声波,聚焦于点zs处,所以可以将公式中的透射响应TA(zs,z0,t)的时反用下行聚焦函数代替。同理定义聚焦函数的上行分量f−1(z0,zs,t),表示聚焦点在zs处的向外扩散的波场,它是聚焦函数的下行分量通过参考介质表面反射序列得到的响应,所以将推导过程中的中间变量RA(z0,z0,t)f+1(z0,zs,t)用f−1(z0,zs,t)代替。聚焦函数表达式中的第二项zs表示此函数的聚焦点,这两种聚焦函数的定义会方便后续的求解过程。
将上述不同状态、不同位置处记录的波场分量代入等式(1)和等式(2),可以将“状态B” 中深度为0 m 处记录的反射响应R(z0,z0,t)和深度为900 m 处的接收器接收的介质表面声源发射的单程格林函数G±(zs,z0,t),通过定义在“状态A”中的聚焦函数f1±(z0,zs,t)联系起来。因为本文将方程求解过程限制在一维介质,所以得到一维时域耦合Marchenko方程[3−5]:
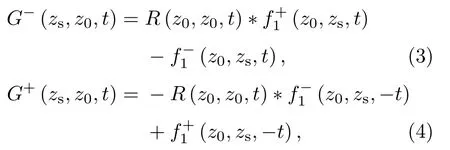
其中,“∗”表示卷积,f1±(z0,zs,t)表示聚焦于深度为zs处的聚焦函数,G±(zs,z0,t)为声源位于z0、 在zs处接收的格林函数。为了书写方便,下文将和R(z0,z0,t)分别简写为G+、G−、f1−、f1+和R。Marchenko 耦合方程组(3)和方程组(4)是欠定的,两个方程,四个未知数:G+、G−、f1−、f1+,接下来将首先展示如何利用实际介质中的反射响应求取两个定义在参考介质中的聚焦函数。
2 聚焦函数重构
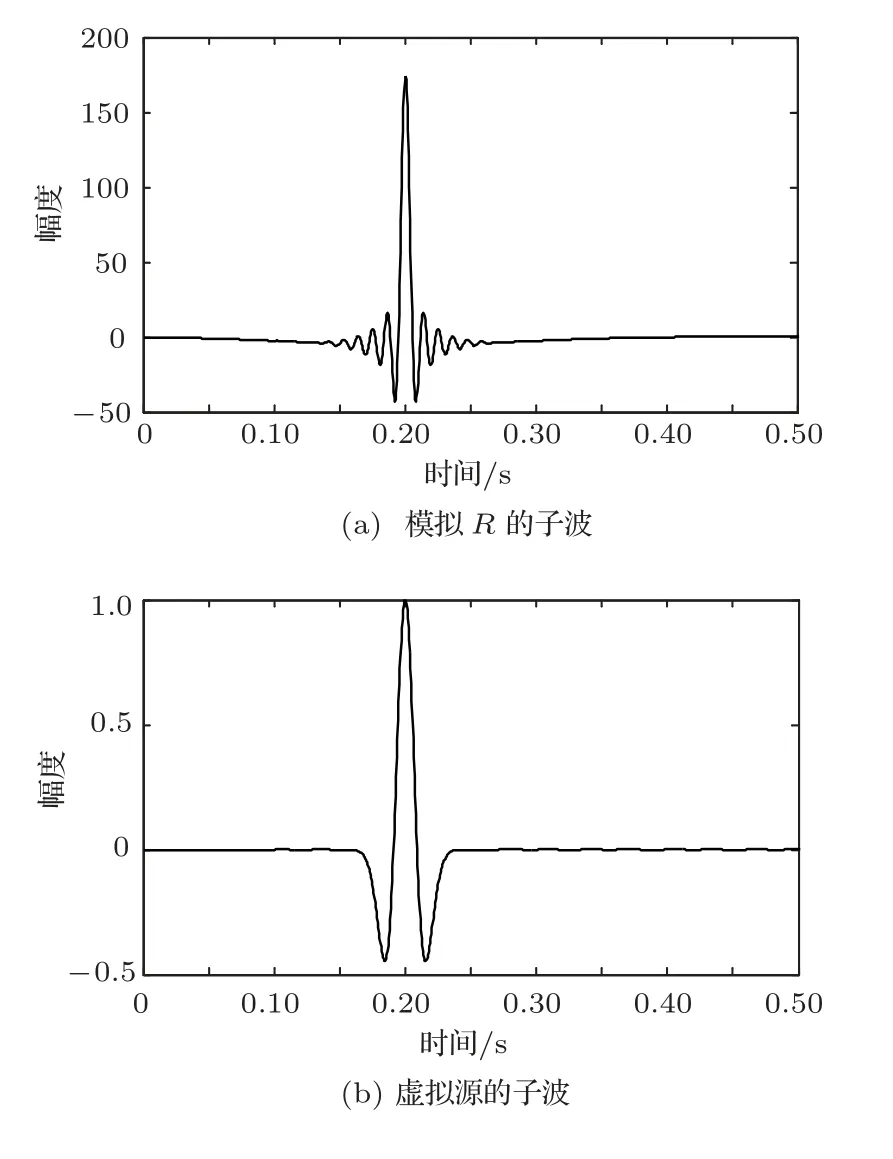
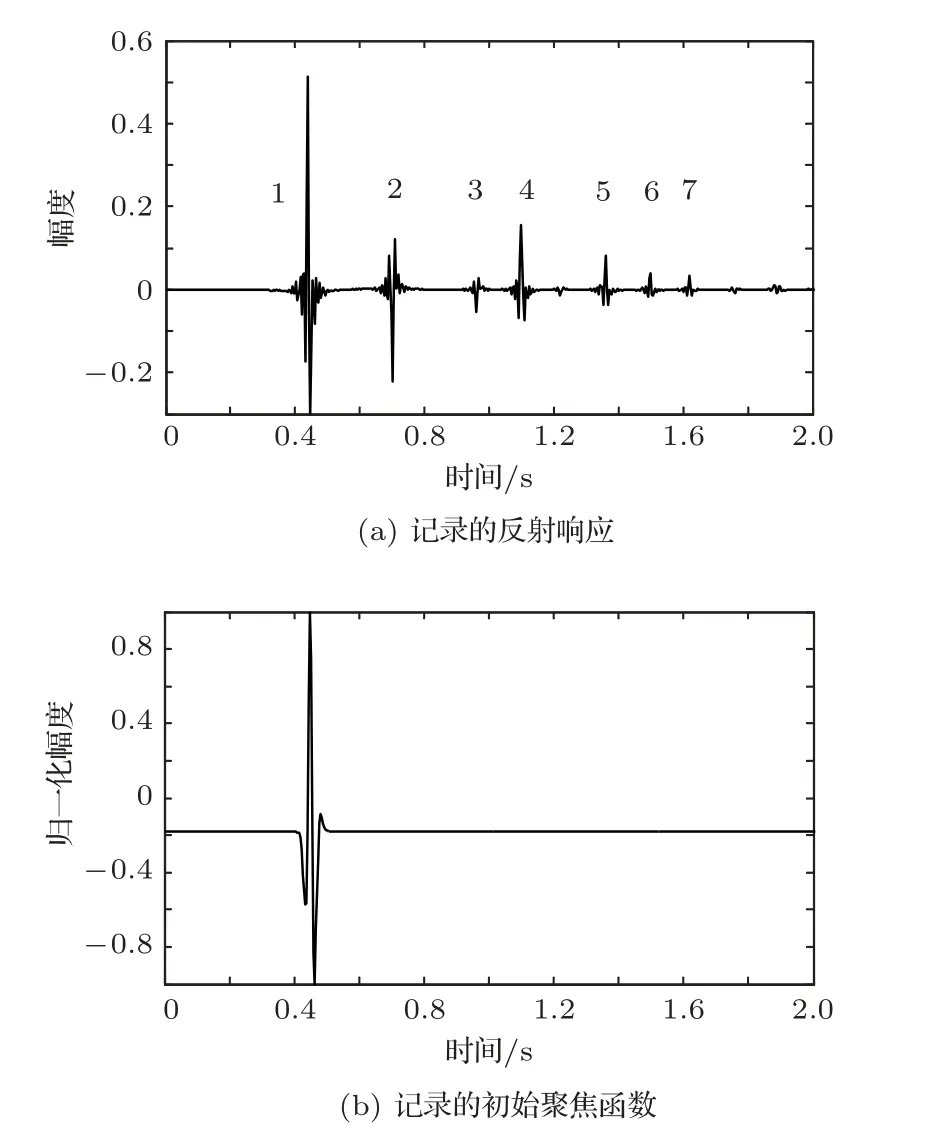
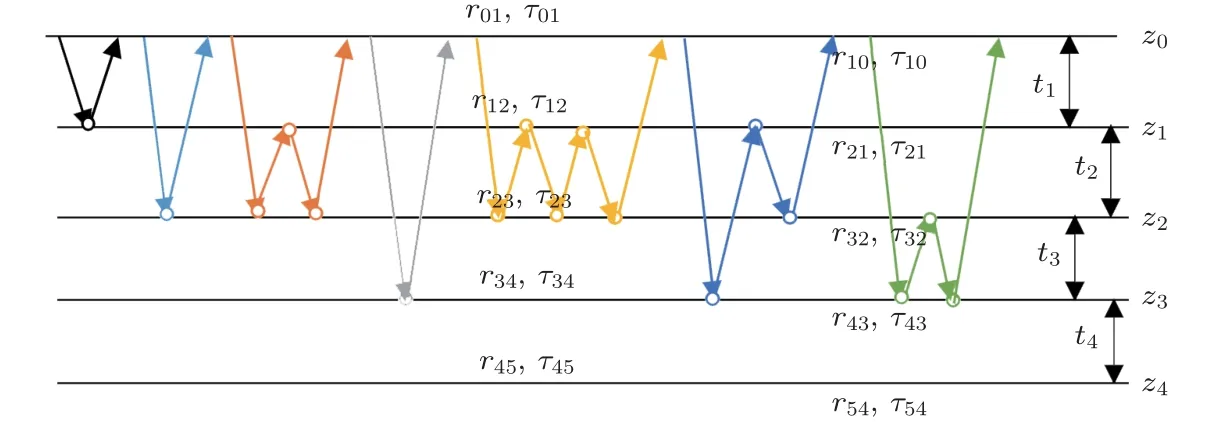
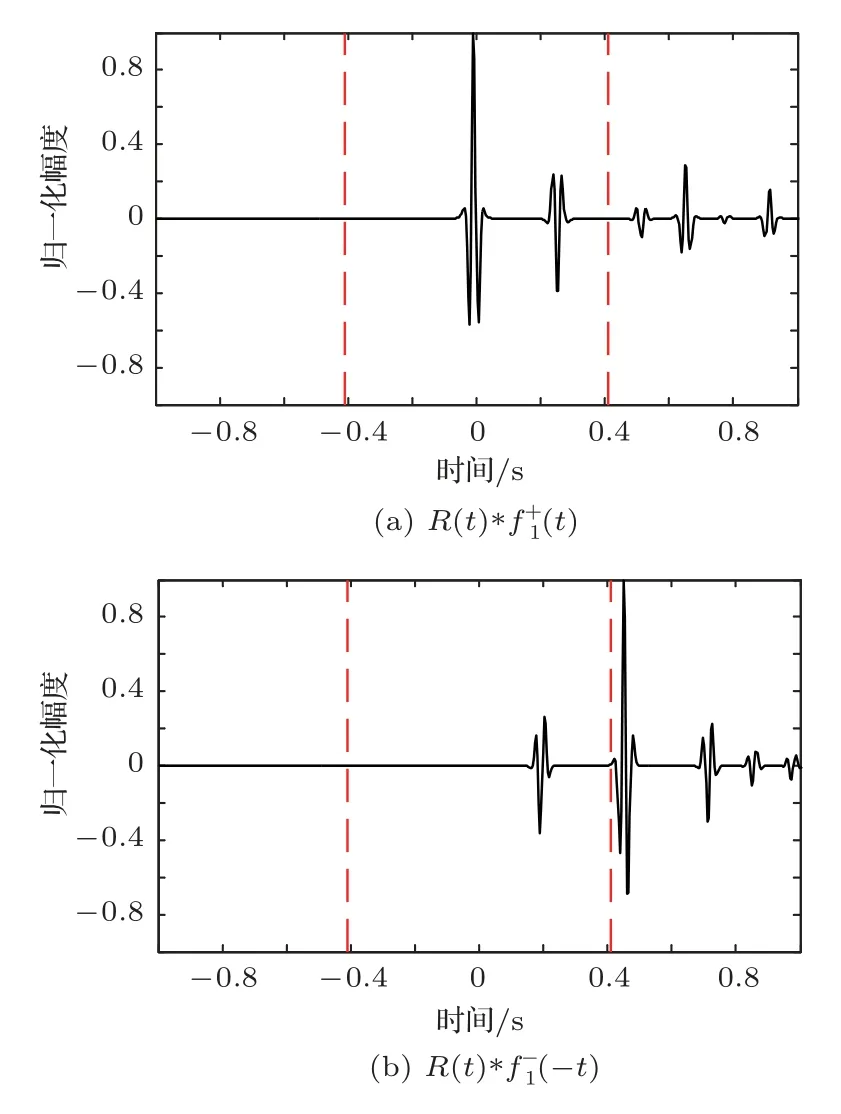
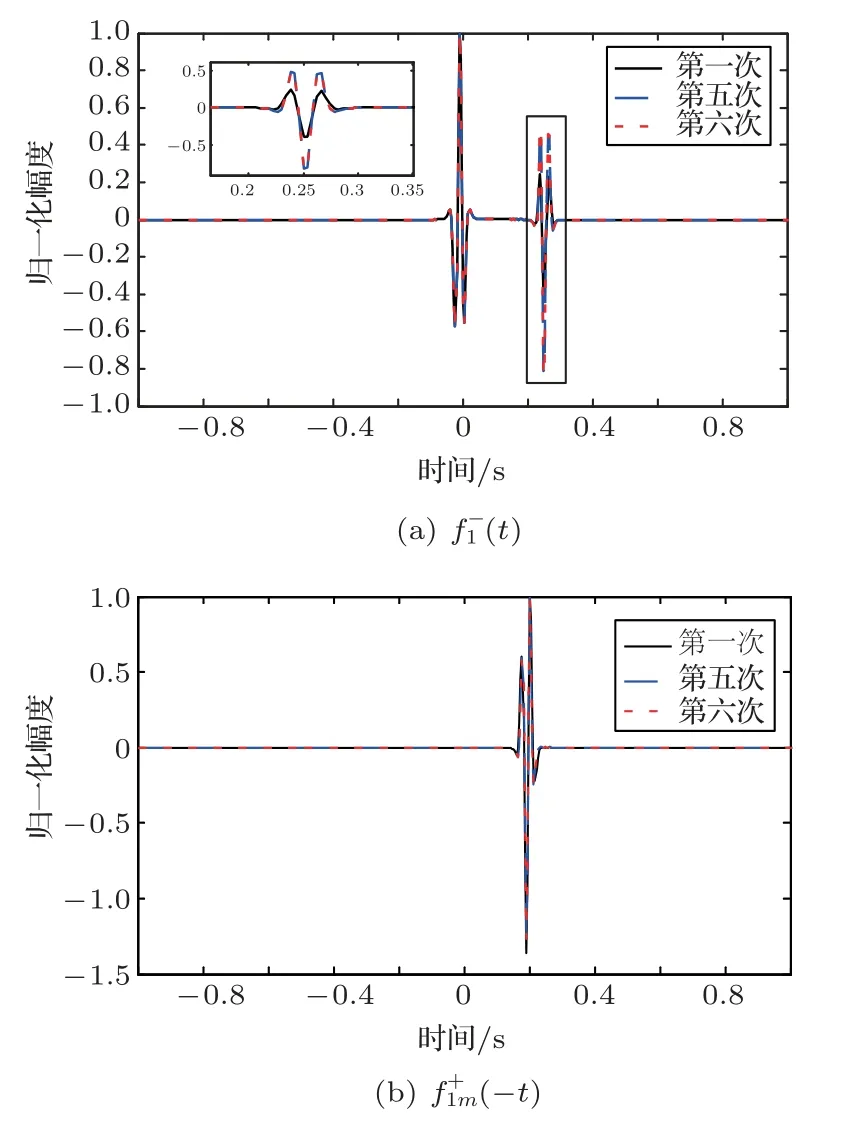
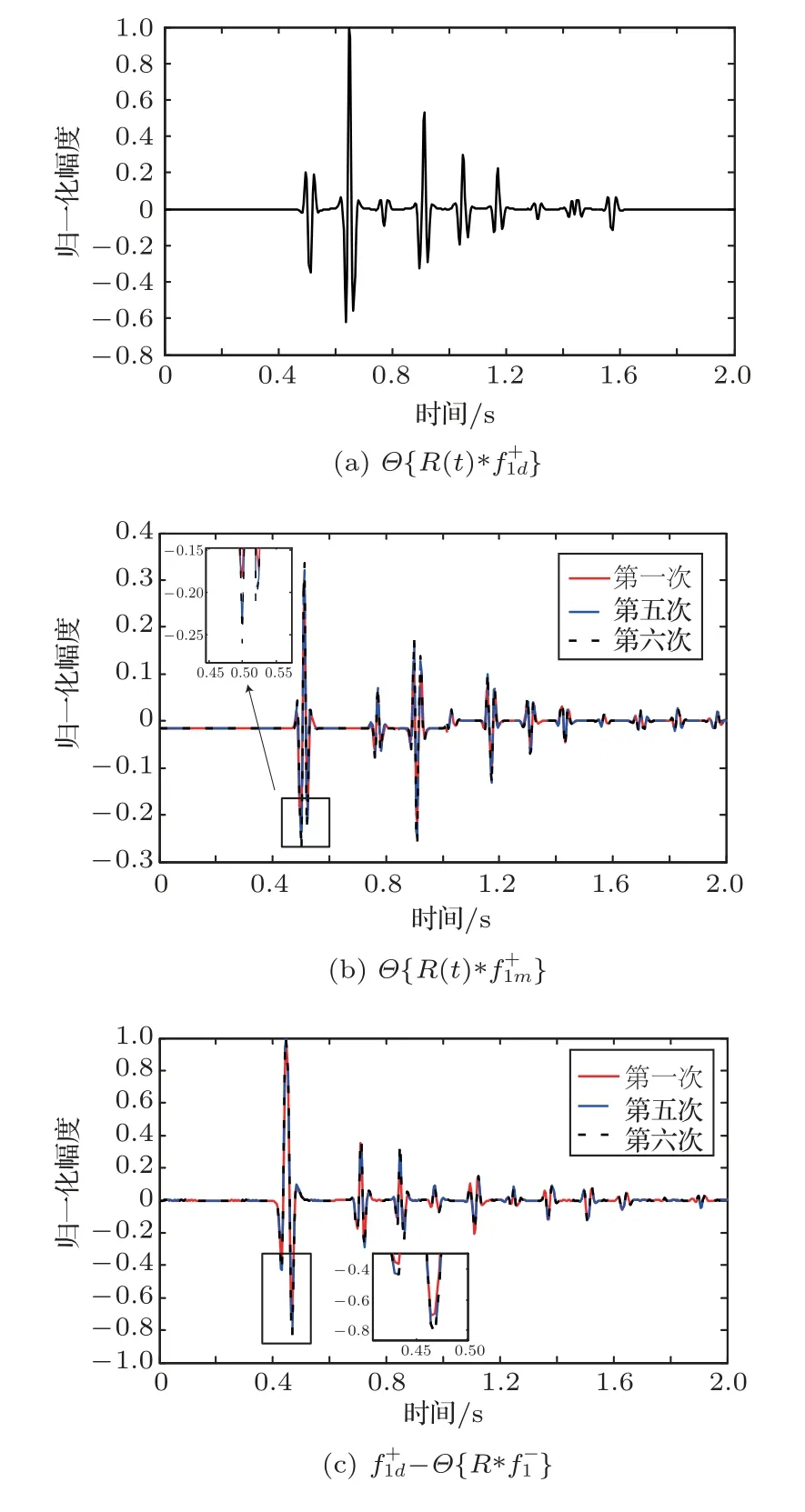
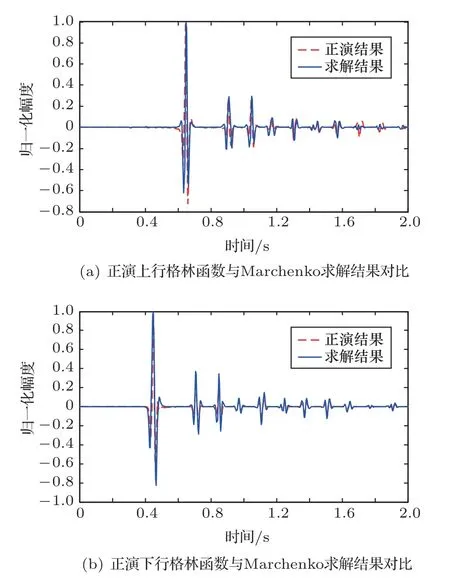
位于zs= 900 m 处的脉冲点源激发的波场直达波将会在t=td(直达波传输时)到达介质表面z0= 0 m 处的接收器,即格林函数中的所有序列将会在t≥td出现在接收记录中。在t 依据上文和van der Neut 等[4]关于聚焦函数的分析,下行聚焦函数是参考介质透射响应的时反波场,它由−td时刻的首波和在−td与td之间的尾波序列构成,将时间窗算子应用于下行聚焦函数可以得到 而上行聚焦函数是在−td与td之间的波场,加窗后为 因此,对于耦合Marchenko方程组(3)和方程组(4),将时间窗算子作用于等式两边最终可以得到 为了求解聚焦函数和,将介质中虚拟点源到介质表面的直达波的时反波场作为初始的下行聚焦函数,同时假定的初始值为0。将接收的反射响应R(t)和初始聚焦函数的估计代入等式(7),可以得到的首次更新,然后将代入等式(8),得到的第一次更新值。接着,将第一次迭代求得的与求和,可以得到的全波场,再代入等式(7)就可以得到的第二次估计,然后再代入等式(8)得到的第二次更新,就这样依次进行迭代求解,直到聚焦函数收敛且达到稳定状态。 假定图1(a)所展示的数值解模型是无损的,且不考虑自由表面多次波的影响,利用时域有限差分算法[9]正演模拟反射响应R(t)和初始聚焦函数。数值求解Marchenko 方程时,反射响应R(z0,z0,t)需要子波反卷积,这里采用宽带零相位子波作为声源[10],避免子波反卷积对反射响应造成的误差影响,而且较宽的频带将不会在时域上产生较长的时宽,子波时域图如图2(a)所示。初始聚焦函数可由宏观速度模型计算[3],这里直接运用图1(a)的参考介质正演。模拟初始聚焦函数的源子波设置为中心频率为25 Hz 的雷克子波,子波时域图如图2(b)所示。 图2 模拟反射响应R 和初始聚焦函数的源子波Fig.2 Source wavelet for simulating the reflection response R and the initial focus function 图3展示了得到的介质表面记录反射响应和直达波,它们将作为迭代求解Marchenko 方程的初始输入数据。通过分析图3(a)中反射响应的记录和一维介质的分层信息,得到图4中的多次波序列解析解模型,图4中从左到右的彩色箭头分别表示图3(a)中的前七个波序列。对于文中的一维模型,zi表示深度,下标i= 0,1,2,···对应1D 模型的深度,其中z0是接收面,t1、t2、t3、t4分别代表声波在各层的单程传输时,r01、r12、r23、r34、r45和τ01、τ12、τ23、τ34、τ45分别是按深度增加方向的各层的反射系数和透射系数,r54、r43、r32、r21、r10和τ54、τ43、τ32、τ21、τ10分别是按深度减小方向的各层的反射系数和透射系数。 图3 迭代求解的初始输入Fig.3 Initial input of iterative solution 图4 1D 解析解模型Fig.4 1D analytical model 图1(a)中的数值解模型中表面记录的反射响应可以展开为图4解析解模型中各个序列的和, 为了更清晰地展示反射响应中各个序列幅度对合成波场的影响,将等式(9)中用反射系数和透射系数表示的各个序列幅度用RAi(i=1,2,3···)表示,即 聚焦点位于深度z2和z3的中心处,聚焦点到表面接收点的直达波可以表示为 依据上文的解释,将直达波的时反序列作为初始聚焦函数,即: 幅度τ21τ32用表示。 第一次迭代,将反射响应和初始聚焦函数代入等式(7)可以求得f1−(t),这个步骤相当于将反射响应沿着时间轴逆向移动直达波的到时,即移动相位,加时间窗算子θ{·}后可得到这两个序列构造的f1−(t): 由等式(11)得到的f1−(t)有两个序列,幅度分别为因为声波透射系数恒为正,依据图1(a)模型中各层的声阻抗的值,可得,可知f1−(t)中两个序列的幅值一正一负。接着,将f1−(t)时反后代入等式(8),相当于反射响应分别与f1−(−t)中的两个序列分别卷积(相移)再求和,加窗后可得 本模型中,通过计算可以发现(−t)的相位是由反射响应中第一个序列与f1−(t)中的第二个序列构造的,即将反射响应中的第一个序列的相位移动,依据反射系数和透射系数的值可以判断的幅值 图5 第一次迭代后的结果Fig.5 The result after the first iteration 图5是基于数值解模型求解的第一次迭代后的结果,图中绘制了两条红虚线表示时间窗算子θ,两条线在时间轴上镜像对称,窗算子θ去除正负窗口外的所有数据,而仅仅保存窗口之间的数据。利用时间窗算子截取窗内部的序列只得到两个序列(图5(a)),这就是首次迭代更新的上行聚焦函数f1−(t)。与图3(b)中的初始聚焦函数相比较,发现第一个序列的幅值是正数相乘的结果,而第二个序列是负数相乘的结果,与对等式(11)两个序列的幅度分析结果一致。接着将这两个序列时反,得到f1−(−t),将它和反射响应卷积可以得到图5(b)的结果。两个序列和反射响应序列的卷积可以分为单个序列卷积的和,也相当于将反射响应序列在时间轴上移动相位后再求和。窗算子作用后只留一个序列,即(−t),时反后就可得到(t),幅值为负数相乘的结果。数值求解的结果与等式(11)和等式(12)的结果相同。本质上来说,来自反射响应的序列随着首波到达时间而移动,以构建序列。由于首波是时反非因果的,因此它会将反射系列中的所有序列向负时间轴移动。其中的一些序列变得太多,以致变为非因果序列。接下来又计算了第二、第三次迭代,得到具有相同相位而幅度不同的f−1(t)和(t)。 第二次迭代, 首先将第一次迭代求得的(−t)时反后与(t)求和可得 由等式(7)可得 接着将等式(14)得到的f−1 (t)代入等式(8)可得 第三次迭代,首先将等式(15)得到的(−t)与(t)求和: 由等式(7)可得 接着将等式(17)得到的f1−(t)代入等式(8)可得 将经历多次迭代后的f−1(t)与(−t)作为最终的聚焦函数,求取期望的格林函数。对比三次迭代结果,等式(11)、等式(14)和等式(17)得到的f−1(t),发现每次迭代得到的下行聚焦函数的序列都只有两列,且相位完全相同,而且第一个序列的幅度也是完全相同的,等式(14)中第二个序列的幅度是等式(11)得到的序列幅度基础上再加一个第三次迭代的结果是第一次结果的基础上对上一次迭代的幅度进行微调,而不影响相位。同理,对于等式(12)、等式(15)和等式(18)得到的(−t),只有一个序列,幅度在每次迭代后进行微调。 数值模拟实验中,总计迭代计算了六次,抽取其中第一、第五和第六次结果,在图6中对比,不同的颜色分别代表不同的迭代结果。对于图6(a)中的f−1(t)只有两个序列,第一个序列幅度和相位完全重合,第二个序列的幅度有轻微的差别,将图中第二个序列放大得到6(a)图中左边插图展示,可以发现幅度差别很小,第六次迭代结果已经收敛于第五次迭代。在图6(b)中,只有一个序列,幅度差异很小,不同的迭代结果在到时和波形上匹配很好,数值解的图形很好匹配了解析解的分析结果。 将在时间轴上与窗算子θ相逆的算子记为Θ,Θ去除了直达波到达前的所有序列,而不包括直达波本身。可用来求解位于算子θ外围的格林函数。将Θ置于Marchenko 方程组(3)和方程组(4)两端,可以得到 图6 不同迭代结果对比Fig.6 Comparison of different iteration results 和 通过等式(7)和等式(8)的三次迭代求解得(t)和f1−(t),结合已知的R(t)和(t),代入等式(19)和等式(20),就可以得到单程格林函数。为了更加清晰地描述迭代过程的特点,只取迭代结果的前三个序列,具体解析解求解过程如下。 首先(t)的初始值为0,第一步可用R(t)和卷积后,加窗算子Θ求取上行格林函数,得到 正如上文所描述的,这个步骤相当于将反射响应沿着时间轴逆向移动直达波的到时,即移动相位,加窗算子Θ作用后求取算子θ外围的的波场序列。依据等式(12)求得的(t),可以求得Θ{R(t)(t)}第一次迭代计算的结果: 对比等式(21)和等式(22),可以发现等式(22)中前三个序列中没有等式(21)中的第二个序列,同时对于等式(21)和等式(22)中的第一个序列,幅值,幅值,对于等式(21)中第三个序列和等式(22)中第二个序列的幅值,接着由等式(15)的结果,得到第二次迭代后的结果: 利用等式(18),得到第三次迭代后的结果: 接着可以将等式(10)和等式(13)两次求得的f1−(t),结合已知的R({t)代入等式(20),}首先可以分别得到三次迭代的ΘR(t)∗f1−(−t),具体结果如下。 第一次迭代: 第二次迭代: 第三次迭代: 对比等式(25)、等式(26)和等式(27),三次结果的前三个序列的相位完全一样,而幅度差异很小。接着可以基于等式(20),利用已知的(−t),减去上文求解的Θ{R(t)∗f1−(−t)},得到下行格林函数。(−t)的相位为与第一个序列的相位完全相同,所以相减操作是为了校正第一个序列的幅度,同时将后续的幅度乘以−1,使子波的幅值归位。 图7 格林函数序列不同迭代结果对比图Fig.7 Comparison of different iteration results of Green’s function sequence 接下来,将上文基于Marchenko 方法迭代求解的上下行格林函数和正演模拟波场分离[8]的结果进行对比,其中红虚线表示正演模拟的结果,蓝实线表示由Marchenko方程求解结果,如图8所示。 从图8中,发现蓝实线表示的基于Marchenko方程求解的上行和下行格林函数迭代求解的结果,和正演模拟的结果在波形和相位上吻合很好,说明了一维Marchenko 方程准确地分解了虚拟源位置接收的波场。如果将上行格林函数和下行格林函数求和,可以得到点源激发的全波场。 图8 Marchenko 方程求解结果与正演结果对比Fig.8 Comparison of the results of the resolved Marchenko equation and the directly model 本文通过一维声学介质的数值解和解析解模型对耦合Marchenko 求解单程格林函数过程进行了详细的讨论和说明。可以得到以下五个结论: (1)在欠定方程组不可求解的情况下,可以基于聚焦函数和格林函数的波场因果性质,通过引入时间窗算子迭代求解耦合方程,时间窗算子内部计算聚焦函数,外部计算格林函数; (2)通过对不同迭代次数的聚焦函数分析,可以发现在第一次迭代后,期望的序列在相位上已经很准确,而后续的迭代过程是对幅度的微小调整,而且聚焦函数内部波形序列的相位差,在后续的步骤中可以去除由层间多次波产生的伪波序列; (3)利用初始聚焦函数计算的上行格林函数估计包含了伪波,这些伪波需要利用R(t)(t)的迭代稳定值去除;对于下行格林函数,可以发现在第一次迭代后,期望的序列在相位上已经很准确,而后续的迭代过程是对幅度的微小调整; (4)从解析解等式中可以发现,基于Marchenko方法迭代求解单程格林波场,反射响应和直达波的幅度构造了聚焦函数和上下行格林函数的幅度,因为Marchenko 方法中反射响应是子波反卷积的结果,所以准确的子波反卷积操作对结果很重要; (5)迭代求解Marchenko 方程本质上是通过初始聚焦函数对记录的单边反射响应进行相位调制,接着利用聚焦函数的作用,使反射响应中的序列逐步移位到介质中虚拟接收器接收的波场响应序列。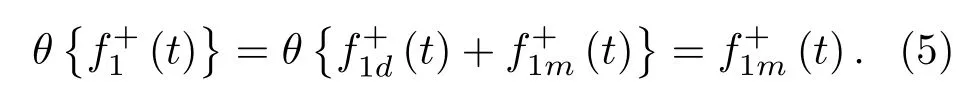
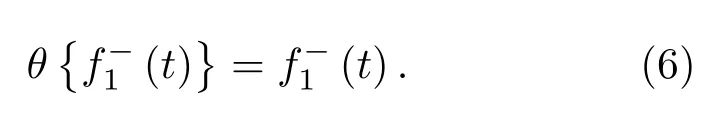
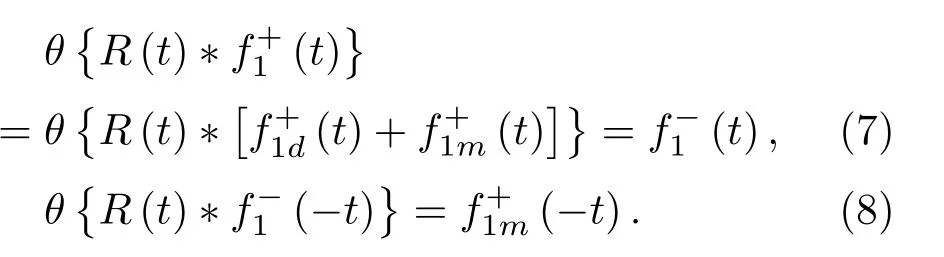

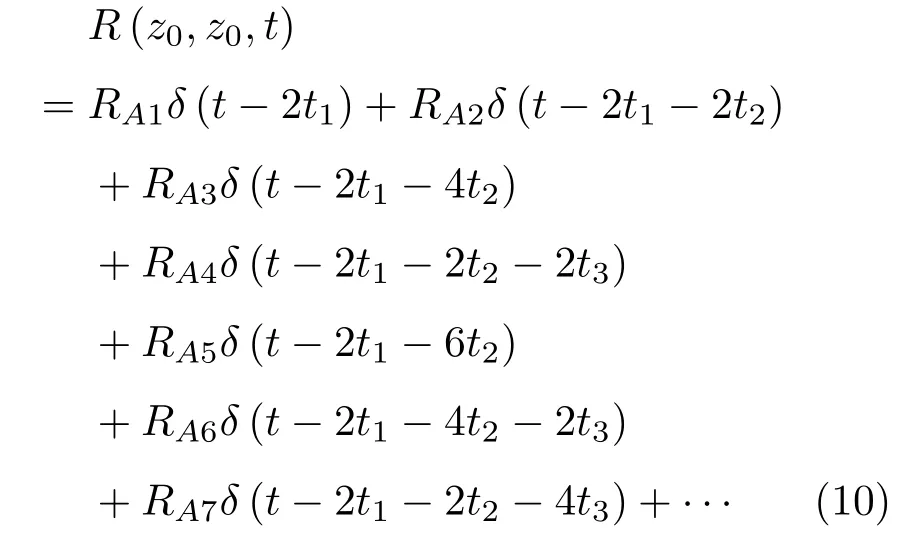
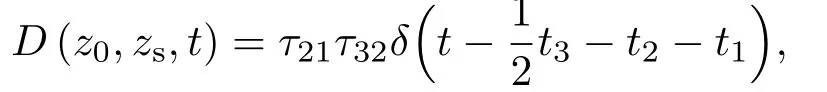
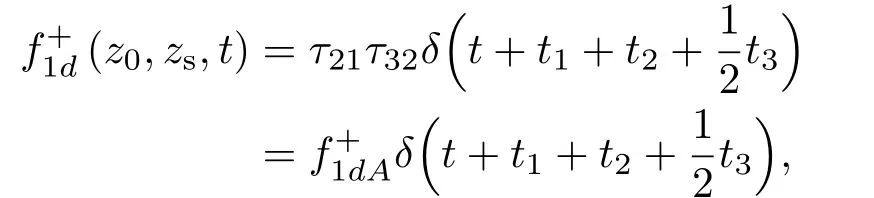
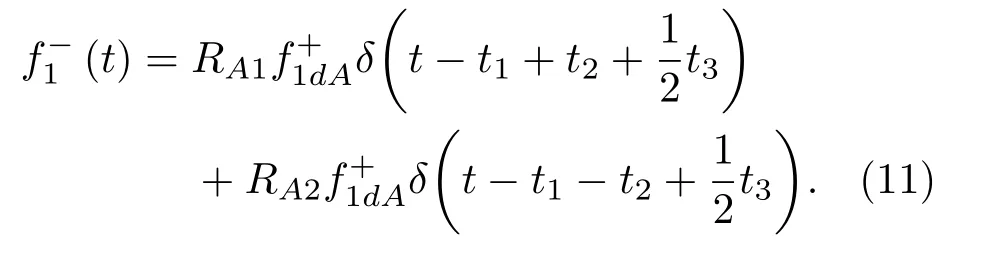
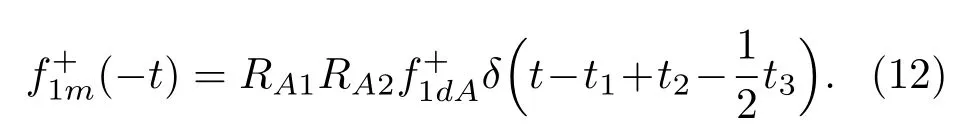
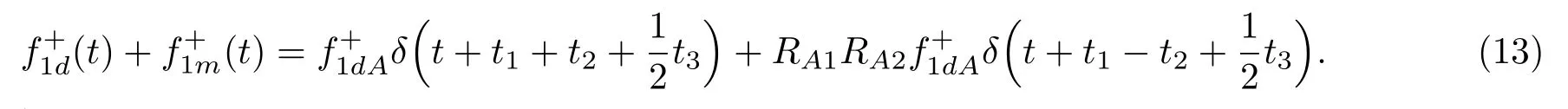
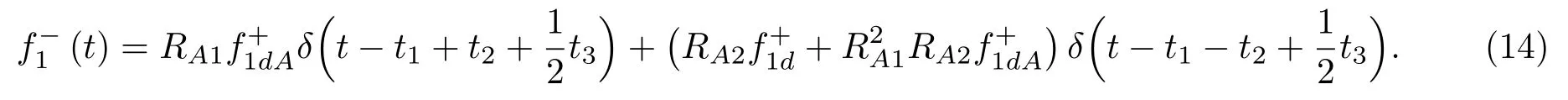
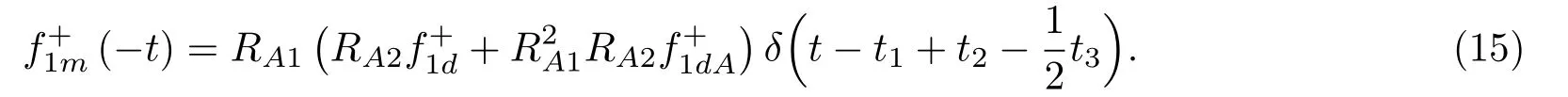
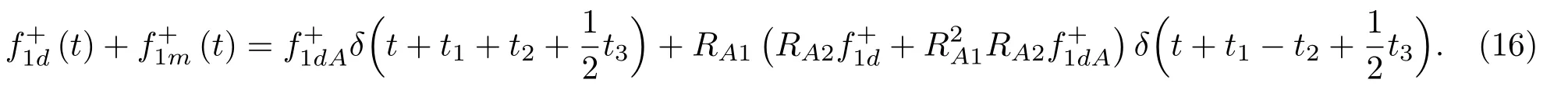
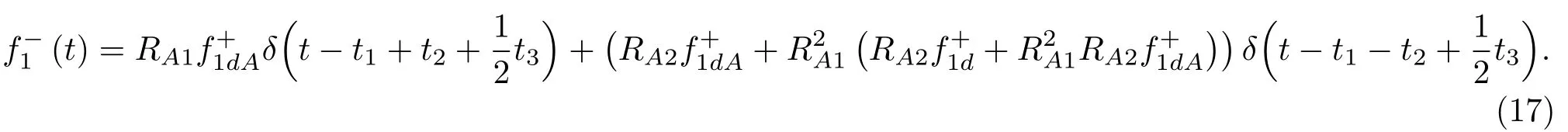
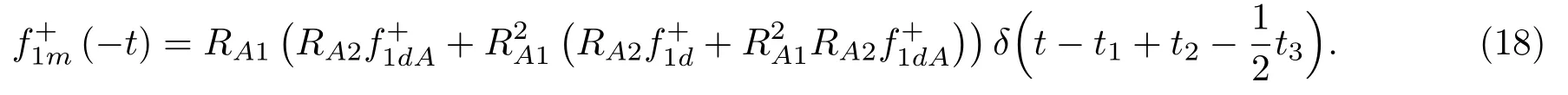
3 单程格林函数重构
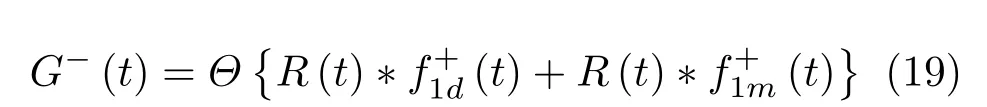
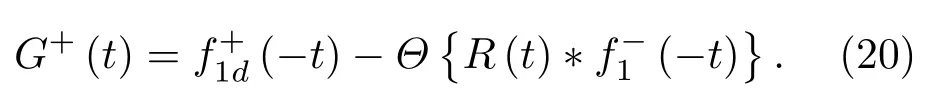
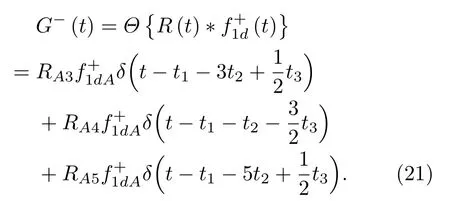
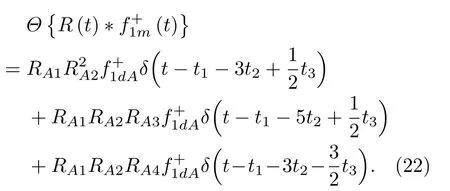
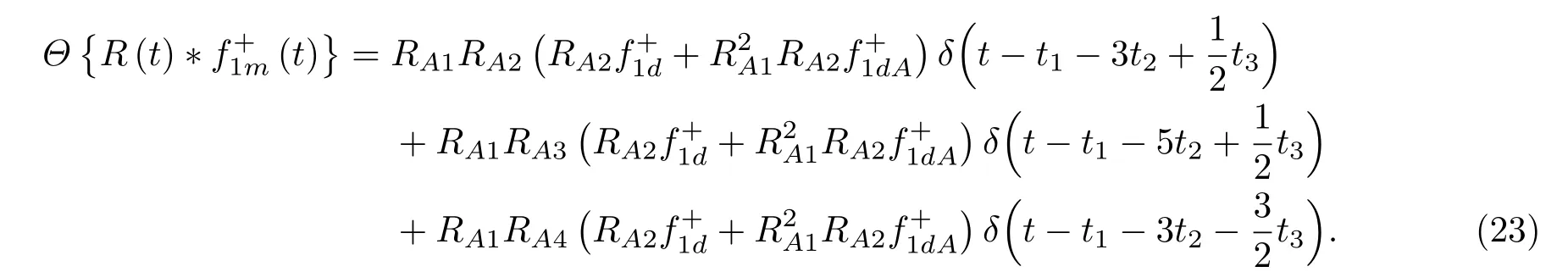
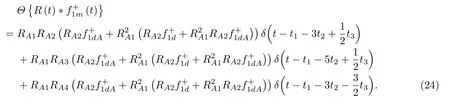
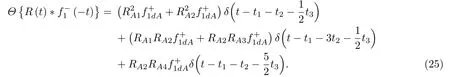
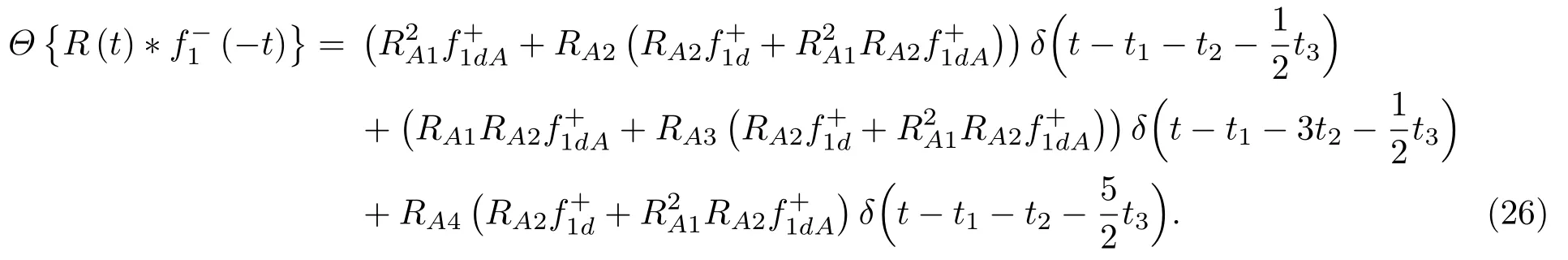
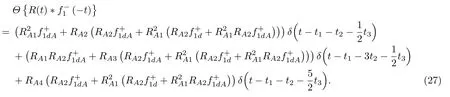
4 结论
