长相依固定设计下部分线性EV 模型的小波估计的渐近性质
2019-11-23刘香胡宏昌余新新
刘香, 胡宏昌, 余新新
(湖北师范大学数学与统计学学院, 湖北黄石435001)
1 引言
部分线性EV 模型如下

这里{yk,k=1,2,···,n} 是观测值,β是一维未知参数,g(t) 是光滑的曲线, {tk} 为区间[0,1]内的序列.{εk,k=1,2,···,n} 表示随机误差, 变量{xk} 不能直接被观测, 只能通过Xk=xk+uk来观测, 其中{uk} 是测量误差, 且假设{uk} 为已知独立同分布的随机变量, 而且对于每个k值, {uk} 与{εk,k=1,2,···,n} 都是相互独立的.假设E(εi)=0, var(εi)=1 (即假定已知).则自协方差函数为

这里0<θ<1 是常数,L(t),t∈(0,∞) 是正的缓慢变化函数, 即
几十年来, 部分线性EV 模型已经被广泛研究, 文献[1–4]用小波估计的方法研究了部分线性回归模型, 在误差序列{εk} 独立同分布时, 得到估计量的大样本性质; 若其误差为鞅差序列, 如参考文献[5], 则使用近邻估计方法来研究了部分线性EV 模型.相依误差的一个重要的特殊情况就是误差为长相依的.这种情况会出现在经济学, 时间序列分析和其他学科领域的运用中, 见文献[6–8].使用小波估计对半参数模型的研究见文献[3, 9].文献[10]是对固定设计下的半参数回归模型使用非参数权函数法和最小二乘法.在一定的正则性条件下, 文献[11]中研究了部分线性模型中参数β和函数g(·) 的估计的弱相合性, 均方相合性和收敛速度, 得到了这些估计的渐近表示和渐近分布; 文献[12]研究了长相依随机设计下的部分线性EV 模型, 得到了参数估计量的渐近表示, 渐近分布和弱收敛速度.本文是在这些文献的基础上, 运用小波估计研究了固定设计下的参数估计量的渐近表示, 渐近分布和弱收敛速度.
2 小波估计
本节中, 我们使用小波方法估计未知参数和非参数.令Ai=[si−1,si]表示区间[0,1]的划分区间, 且由(1.1) 式, 得到

假设Schwartz 空间Sl中存在尺度函数φ(x), 在伴随Hilbert 空间中存在多分辨率分析Vm,它的再生核定义为将(2.3) 式看成一般部分线性回归模型.首先, 假设β已知, 定义g(t) 的估计量为

然后, 通过最小化方法来定义小波估计量
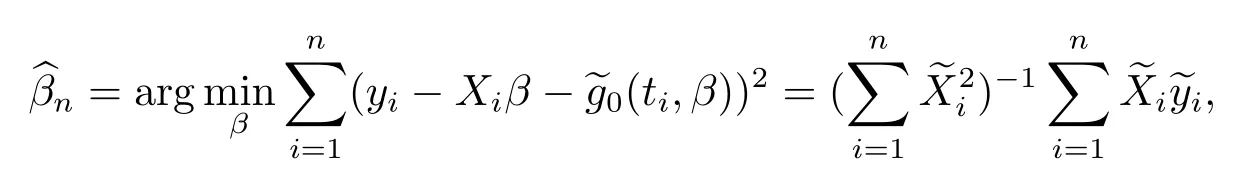
由于在线性回归或在部分线性回归中, 由测量误差所导致的不一致性可由“衰减效应”所克服.因此使用以下修正的最小二乘估计量

最后, 定义g(t) 的小波估计量为

3 主要结果
为了获得主要结果, 作如下假设条件
(1) 令xj=f(tj)+νj,j=1,2,···,n, 这里f(tj) 是区间[0,1]中的函数, 对于实数列{νi}, 有
(2)g(·),f(·)∈Hα(Sobolev 空间),α>1/2;
(3)g(·),f(·) 都是阶数为γ>0 的Lipschitz 函数;
(4) 2m=O(n−1),0<θ 注1条件(2)–(4) 在小波估计中常被用到(见文献[4,10,17,19]).条件(1) 是研究部分线性模型时常用到的条件, 但是本文条件与他们有所不同. (1)文献[9,10,13]均对|νi|p(p≥2) 施加条件, 本文仅对|νi| 施加条件; (2)文献[9,10,13]中对νi施加的条件较多, 本文对νi仅有一个条件; (3)虽然文献[10,13]的条件及文献[9]中的条件A1)i) 均可由本文中νi的条件(条件(1)) 推出(本文中νi的条件比文献[10,13]的条件及文献[9]中的条件1 强), 但本文中νi的条件推不出文献[9]中的条件A1)ii).说明本文νi条件比文献[9]中的条件A1) ii) 弱. 因此文献[9]中条件A1)ii) 不成立. 注2与文献[12]类似, 文献[12]是随机变量, 本文是固定设计. 定理1假设条件(1)–(4) 均成立, 则对任意的α≥3/2, 且有 假设定理1 的条件及结论成立, 则有以下推论, 其中推论1 和推论2 与文献[12]中推论相同. 推论1若{ek,k=1,2,· · ·} 是独立随机变量,G(s)=s, 则对E|uk|4+2δ< ∞,有 推论2在定理1 的条件下, 若uk=0, 则 定理2若定理1 的条件成立, 则对λ/<θ, 且有 为了证明主要结果, 首先介绍一些有用的结论及引理. 首先介绍Hermite 秩的表示和Hermite 级数的一些基本结论.令e表示N(0,1) 上的随机变量, 且G={G:E(G(e))=0,E(G2(e))<∞}, 则G是 构成了L2(R,Φ(s)) 中函数的完整正交系统, 并满足E(Hl(e)Hq(e))=δlqq!. 对任意的G∈G, 令J(q)=EG(e)Hq(e).定义且为G的Hermite 秩.由于J(0)=E(G)=0, 故通常是正数. 令{ek,k=1,2,···,n} 和ρ(k) 如上所述,>0 为固定常数, 则以下结果成立[18]. (F2) 对任意Hermite 秩为<1/θ, 可测函数G∈L2(R,Φ(s)), 特别的, (F3) 对任意缓慢变化函数L(n) 而言, 有 (F4) {Hq(ei)} 是L2(R,Φ(s)) 中的一列随机变量, 且满足 引理1[3]假设条件(3) 成立, 则 引理2假设条件(1) 和(3) 成立, 则xi有界,有界, 且 证由于{νi} 是实数列,f(·) 是阶数为γ> 0 的Lipschitz 函数, 故xj=f(tj)+νj,j=1,2,··· ,n有界.由和引理1(2), 有 引理3令则有 证为了证明此引理, 只需证明注意到 由Cr不等式及引理2, 有 由ui的独立性得 由引理1 及ui的独立性得 引理4[14]假设条件(1)–(4) 成立, 则 引理5[11]假设条件(4) 成立, 则对每个实数a1,a2,···,an, 下列分解成立 这里Tl1,Tl2满足 引理6[13]令表示函数G∈G 的Hermite 秩,ai表示有界的非负实数, 则它的Hermite 秩也是, 且 引理7[15]若G(ei)∈G 的Hermite 秩是, 则 定理1 的证明对由引理2 进行如下分解 由引理6 及(F4) 有 由引理2 及(F4) 有 对Tn3求二阶矩 由引理2 及(F2) 有 由引理6 及(F2) 有 由(5.3)–(5.4) 式可得 对Tn4求二阶矩 由引理2 及(F2) 有 由引理6 及(F2) 有 由(5.6)–(5.7) 式可得 对Tn5求二阶矩 由引理2 有 由引理2 及引理6 有 由(5.9)–(5.10) 式可得 由(F4) 有 对Tn7求二阶矩 由(F2) 有 由(5.12) 式及(F2) 有 由(5.14)–(5.15) 式可得 对Tn8求二阶矩 由(F2) 有 由(5.12) 式及(F2) 有 由(5.17)–(5.18) 式可得 对Tn9求二阶矩 由引理2 有 由(5.12) 式及引理2 有 由(5.20)–(5.21) 式可得 对Tn10求二阶矩 由(5.12) 式, 有 由(5.23)–(5.24) 式可得 由(5.12) 和Chebyshev 不等式可得 定理1 证毕. 推论1 的证明由(3.1) 和(5.28) 式, 有 因此由(5.29)–(5.30) 式得推论1 成立. 推论2 的证明由(3.1) 和(5.28) 式, 有 因为 且 因此由(5.31)–(5.32) 式得推论2 成立. 定理2 的证明 注意到 因为 所以有 从而 由上式和引理2 有 由引理6 和引理7 有 由引理1 有 因此由Markov 不等式和(F3) 可得 由引理1, 可得到 定理2 证毕. 为了对本文的证明结果做进一步的解释和验证, 选取2013 年5 月到2018 年8 月之间的全国居民消费价格指数, 城市居民消费价格指数和农村居民消费价格指数, 使用Mathmatic来做模拟应用(具体数值见东方财富网《中国居民消费价格指数》). 使用下述的式子 其中设全国居民消费价格指数为y, 城市居民消费价格指数和农村居民消费价格指数为矩阵X, 通过X, 由Mathmatic 算得 图1: (t) 的散点图 相对误差H由下式算得 64 个数据中有55 个在0.05%以内,占总数的85.94%;有9 个在0.1%以内,占总数的14.06%,在一定程度上说明估计出的和(t) 是有效的.这个例子也直接说明了本文前面所证明的结论是正确的, 对于数据处理预测也有实际的作用. 具体计算的结果如下表1. 表1: 相对误差表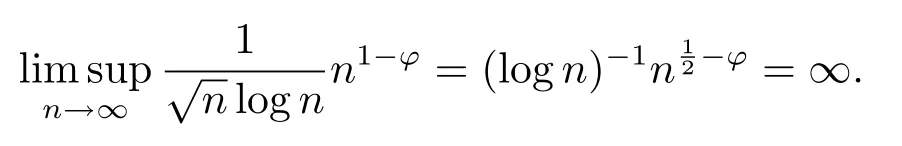

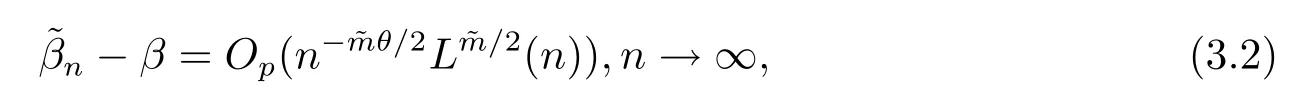
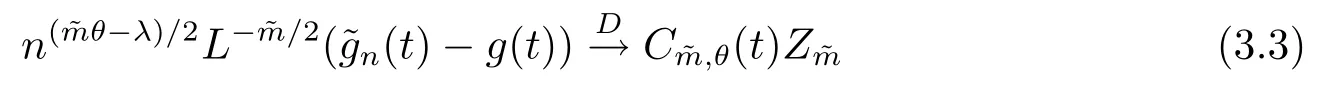

4 主要结果证明所需的引理



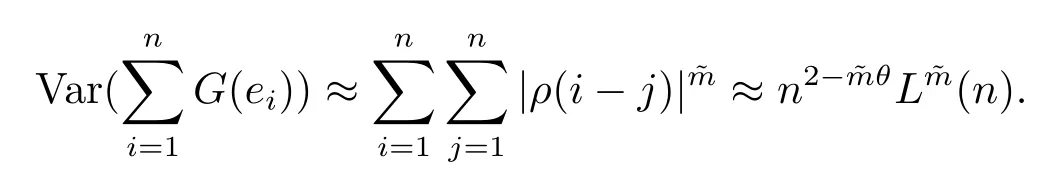




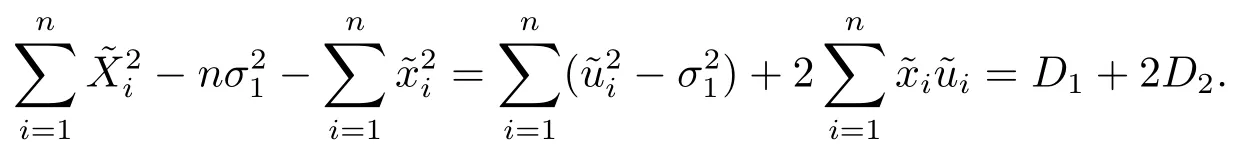
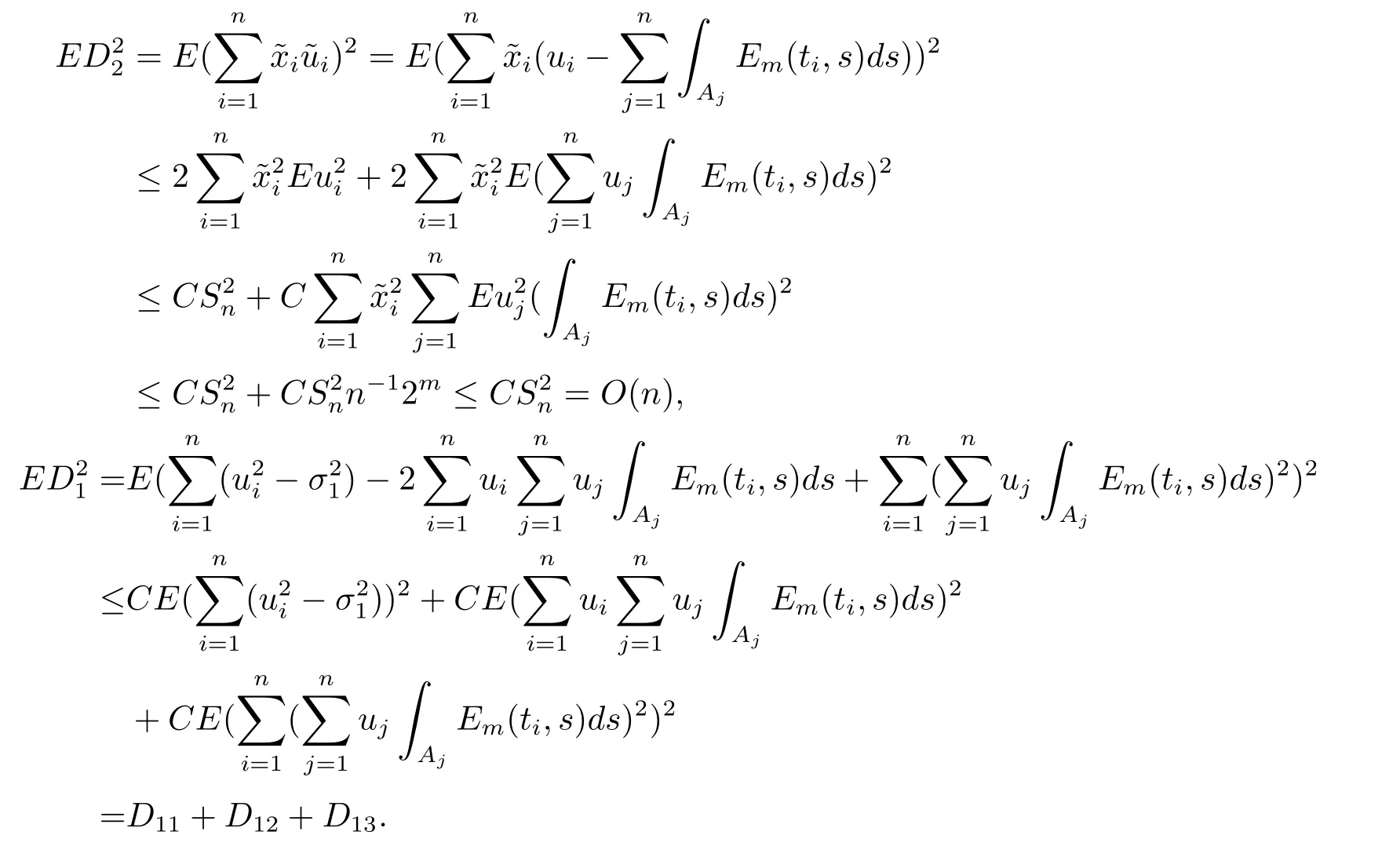




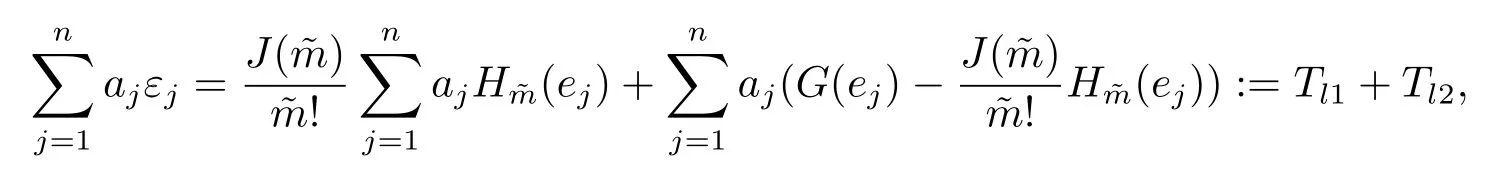
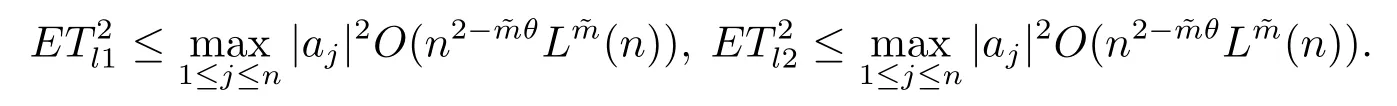


5 主要结果的证明




















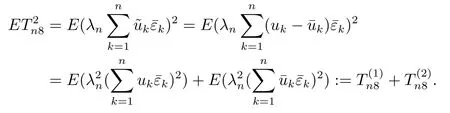

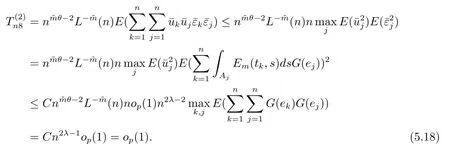






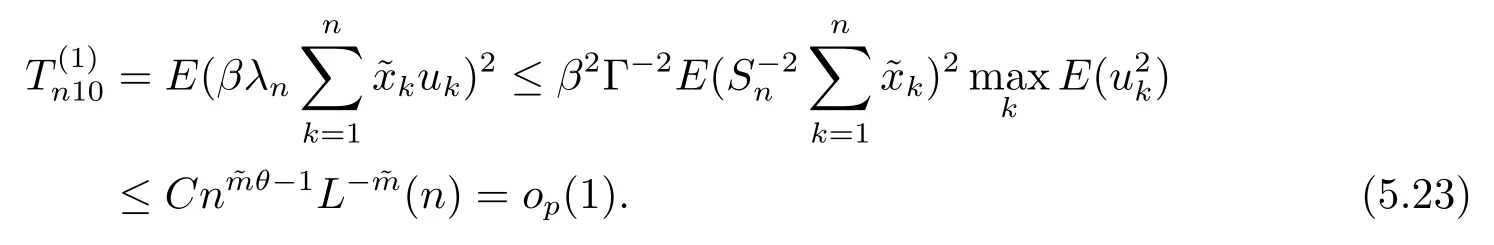
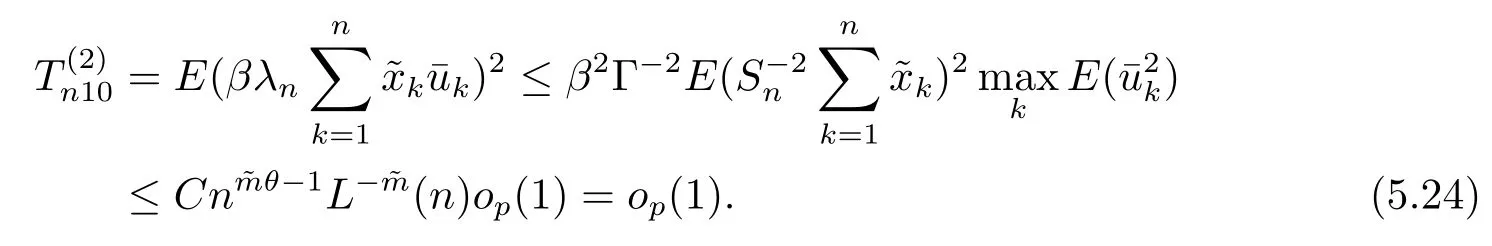






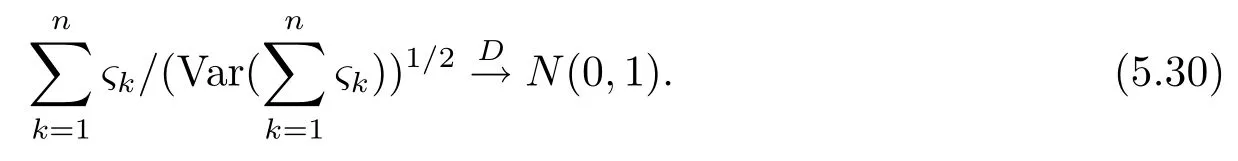








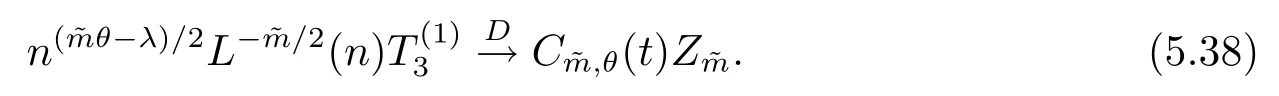


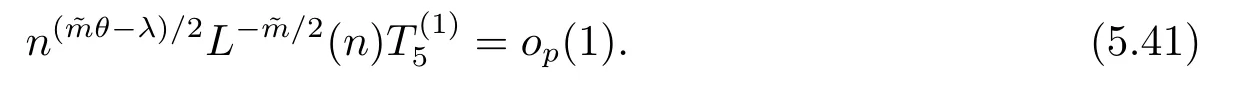
6 模拟例子