李清华 葛君琰

摘  要：“新工科”建设旨在培养多元化、创新型卓越工程人才，线性代数是培养工程人才的数学基础课程。文章介绍了“新工科”背景下线性代数教育教学现状，在分析大学生学习心理以及教学范式改革的基础上，针对培养学生理论联系实际的能力，提出将数学建模思想融入线性代数的现代教育理念和实践路径，并列举了创新性的数学建模思想融入线性代数教学的案例。

关键词：新工科;心理认知;数学建模思想;线性代数

作者简介：李清华，烟台大学数学与信息科学学院副教授，研究方向为模糊拓扑学、模糊凸结构等;葛君琰，烟台大学数学与信息科学学院学生。（山东 烟台 264000）

基金项目：本文系烟台大学2017年度教改项目“在应用型本科院校线性代数教学中融入数学建模思想的研究与探析”（编号：jyxm2017001）和2018年度山东省本科教改重点项目“新工科背景下线性代数教学改革的研究与实践”（编号：Z2018S049）的研究成果。

中图分类号：G642.0     文献标识码：A    文章编号：1671-0568（2019）24-0036-04

一、“新工科”建设及线性代数教学现状分析

“新工科”是基于国家经济发展进入新常态，高等教育迎来新挑战而提出的教育改革新方向，其目標是培养具有创新能力、高素质的适应经济产业发展的卓越工程人才。“新工科”建设要求提高教育教学质量，并提出新的质量标准，即工程人才培养质量要面向未来。新工科必须通过人才培养理念的升华、体制机制的改革以及培养模式的创新应对现代社会的快速变化和未来不确定的变革挑战。[1]

作为“新工科”建设的重要内容，线性代数课程作为普通高校理工、经济和管理等专业的一门基础数学必修课，对数学文化的普及、学生抽象思维的培养等具有不可替代的作用。随着我国经济发展进入新常态，线性代数已经广泛应用到金融、经济、信息等领域。

受传统教学习惯的影响，目前线性代数课程主要围绕知识信息的传授，对理论背后思想及其实际背景意义讲授较少。对于课时少、抽象难懂的线性代数教学而言，如何通过改进教学方法，激发学生学习兴趣，让学生能够轻松接受所学内容，并且能够运用其解决实际问题，为新工科建设发展打下坚实的基础显得尤为重要。

二、基于学习心理需求的教学模式改革

社会越来越关注教育质量，大学生学习行为的投入与学业成就息息相关，大学生学习心理是影响其学习的主要因素之一。大学生学习心理是指大学生在学习过程中受各种内在与外在的、智力与非智力因素影响或刺激而形成的心理反应。探究大学生的学习心理，对提高学生学习能力、改善教学方法具有重要作用。

当前大学生学习方面出现了一些困扰问题，体现出复杂性、矛盾性、变化性、消极性的特点，主要表现在以下方面：①缺乏学习动机，学习目的不明确。学习动机过于功利化，只停留在满足愿望的层面。学习内容多关于社会实惠性、功利性方面，只是为了考试而学习，仍倾向于应试教育。②缺乏学习兴趣，对于学习内容最多只能应付考试，并不能将其应用到现实生活中。③学习内容浮浅，缺乏自学能力。受应试教育的影响，学生一味地等待教师灌输知识，缺乏自己动手探索新知识的精神。[2]

新工科背景下以培养人才为目的的线性代数教学改革，通俗而言是教学范式的根本转型，即从“知识传递型”教学转变为“知识建构型”教学。作为一种行为主义教学观的“知识传递型”教学，知识主要靠练习获得，教师的作用主要是传递知识，学生只是程序性地获得知识，学习动机主要靠外部强化;“知识建构型”教学是一种认知主义教学观，习得知识主要靠自主建构，学生要结合自身已掌握知识形成知识网络框架来获取新知识，教师的作用转变为引导学生建构知识。在科技发达、信息量巨大的当下，教育方式必须转变，才能适应新工科背景下应用型人才培养的新要求。因此，在新工科背景下，结合大学生的学习心理认知，将数学建模新思想融入线性代数中具有很强的实际意义。

三、数学建模思想与线性代数教学融合路径

理论联系实际，知识紧扣应用。数学建模不仅使学生掌握抽象的代数知识，还可以培养学生的运算能力和综合运用所学知识去分析、解决问题的能力，两者的融合可从以下三个路径开展：

1.结合实际问题，激发学生的学习兴趣。线性代数本质是实际问题抽象出来的数学语言，要想增强对这门课的理解就需要适当地回归到实际问题中，厘清每个概念定理的背景，自然而然地引入每个知识点。引入最新科技前沿的案例，引导学生挖掘线性代数的丰富内涵，让学生体会到线性代数的广泛应用，激发学生的学习兴趣，培养他们的实践应用能力。如在讲解矩阵的乘法时，可以结合图像的变换。随着电子科技的不断发展，图形的几何变换应用在动画片制作、仿真模拟设计、电子游戏开发等诸多领域，图形的平移、旋转、缩放等都能由矩阵实现，这能够让学生很好地理解矩阵乘法概念及其在实际生活中的用处;再如讲授矩阵的逆时，教师可以结合密码的编译，说明矩阵的破译过程就是求逆的过程，让学生深刻掌握这一概念。

2.通过模型建立，引入理论知识。在线性代数教学中融入数学建模思想，促进理论知识与实际问题的结合，利用讲解一道数学建模问题引出所学知识点，更加深了学生对知识点的印象与理解。例如，可以通过网络流模型引出线性方程组求解问题的讲解。在交通、电力、运输、通讯、城市规划、任务分配以及计算机辅助设计等诸多领域，网络流模型得到广泛应用，给工程问题的解决带来诸多便利，一个网络由一个点集以及连接部分或全部点的直线或弧线构成，大多数网络流模型中的方程组包含数百个线性方程，要确定每一分支的流量就是解线性方程组，利用矩阵的一些特性，自然而然地引入线性方程组的相关知识点。

3.加强建模训练，培养动手能力。仅仅通过教师的讲解，学生可能只是一时豁然开朗，并不能自己去解决实际问题，还需多加训练。因此，课后作业可以不再只布置一些与考试有关的内容，而应增加学生自主学习的机会，布置一些贴近生活实际的问题，让学生自主动手动脑研究思考，课上交流心得收获，并鼓励学生充分利用现代科技软件进行数学建模分析研究，最终达到学生思维活跃敏捷、动手能力强的效果。

四、“新工科”背景下线性代数教学案例

数学建模思想融入教学是利用数学建模思想来解决数学问题，即将问题简化，根据简化后的问题寻找基本规律，在对客观规律进行分析后，通过表象发现本质，提高学生运用知识的能力。以应用实例来说明。

1.数学建模思想在矩阵计算方面的应用。计算机网络技术快速发展，信息化以及网络数据化已经是大势所趋。上网者主要靠搜索引擎获取信息，获得满意结果的背后主要是PageRank算法在起作用，PageRank算法的搜索结果主要按照网页的重要性来排序，可以通过网页的投票数这一概念来界定网页的重要性，网页投票数可以理解为网页的链接数。PageRank的核心思想是：①若某一网页的投票数即链接网页多就说明这个网页相对重要，即PageRank值较高;②网页的pagerank值会随着链接到其他网页的pagerank值大小变化而变化。简而言之，通过PageRank可以大体计算上网者在各个网页上的概率，上网者先随机打开一个网页，然后在网页上的跳转满足随机性。现假定网页链接是一个有向图，网页是结点，网页间的链接用箭头表示，如图1所示：

求上网者最终在网页1，2，3，4上的概率。

（1）模型假设。

①假设可访问网页总数为[n]，网页[W]能链接到[m]个网页，网络链接矩阵定义为[P=pij∈Rn×n]，其中

[Pij=1m，若网页j有一链接跳转到网页i0，否则（i，j=1，2，3，4）]

②假设网页W的投票数越多，则网页W越重要;

③假设指向网页W的质量越高，则W越重要。

（2）模型建立：

本例中含有4个网页，假设上网者目前在浏览网页1，则此上网者分别有[13]的概率链接到网页2，3，4，其中[13]中的分母3表示网页1可链接到其他3个网页，即若一个网页能连接到m个网页，则随机转到其他任一网页的概率为[1m]，其他网页的跳转概率也可由此方法得到，由此可得上图对应的转移矩阵为：

[P=0  12  1  013  0  0  1213  0  0  1213 12  0  0]

（3）模型求解。

初始时上网者在每一网页的概率假设相等即为[1n]，所以最开始的概率分布为所有值都为[1n]的n维列向量，此例中列向量[Q0=14141414]，则可通过公式[Q1=PQ0]得到跳转一次后的概率分布向量[Q1]：

[Q1=PQ0=][0  12  1  013  0  0  1213  0  0  1213 12  0  0][14141414]=[924524524524]

可见[Pij≠0]表示有一链接从网页j指向网页i，则[q11]表示所有网页到网页1的概率为[924];以此类推，可以求出跳转任意次的概率分布向量，当跳转无穷次时[Q]会收敛，即[Qn=PQn-1]，通过不停地迭代，最终可以得到

[Q=][39292929]

即最终上网者停留在网页1的概率为[39]，在网页2，3，4的概率为[29]。

此例讲解的是最简单的PageRank模型，让学生初步了解了搜索引擎背后的原理，在今后的学习中能够知道所学习的矩阵的用处，灵活运用理论知识。PageRank算法还可运用在城市交通轨道站点选址、基础网络设计等问题中，可提高选址的准确性与有效性。

2.数学建模思想在逆矩阵方面的应用。在科技发达、信息技术不断发展的今天，信息安全问题时有发生，保密通信工作提上日程，保密通信模型是实现信息安全的一种有效方法。矩阵是线性代数课程中的重要内容，是工科中常用的有效工具，其在保密通信模型中有着突出贡献。下面主要介绍融入数学建模思想的可逆矩阵加密技术。[3]

（1）保密通信数学模型。保密通信模型的两个重要组成部分是发送方的明文串和接收方的密文串，加密信息传输过程主要包括发送方将需要传输的信息通过某种自定义算法转换成密文发送给接收方，经过相应的算法，接收方再将接收到的密文转换为明文信息。简要的通信技术模型如图2：

显然要使信息传输有效，密文串必须能被翻译成明文串。假设明文串数据接收方未知为X，密文矩阵为A，有方程[A=BX]，可见[B]为发送方向接收方传送信息的加密矩阵，若[B]可逆方程组有唯一解，[B-1]为接收方的解密矩阵，这样接收方就可通过[X=B-1A]获得明文信息。又由矩阵的乘法可知，要想求出结果，左边矩阵的列数必须等于右边矩阵的行数，所以在设计加密矩阵[B]时应注意此规则。

（2）保密通信数学模型的应用案例。在某次机密谈判中，假设甲方需将明文good加密发出，可将26个英文字母分别与数字1-26一一对应，并且双方假定加密矩阵为：[B=1  21  1]。

甲方要发出去的明文转换为代码分别为7，15，15，4，根据矩阵乘法原则及加密矩阵的阶数，确定明文矩阵为[X= 7  1515   4]，再根据矩阵方程[A=BX]，得密文矩阵[A]：

[A=BX=1  21  2 7  1515   4=37  2322  19]，

也就是最终明文信息以数字代码37，22，25，19发出。

当乙方收到密文矩阵时，可以利用双方协定好的加密矩阵[B-1=-1   2 1  -1]获取有用信息明文矩阵[X]：

[X=B-1A=-1   2 1  -137  2322  19=7  1515  4]

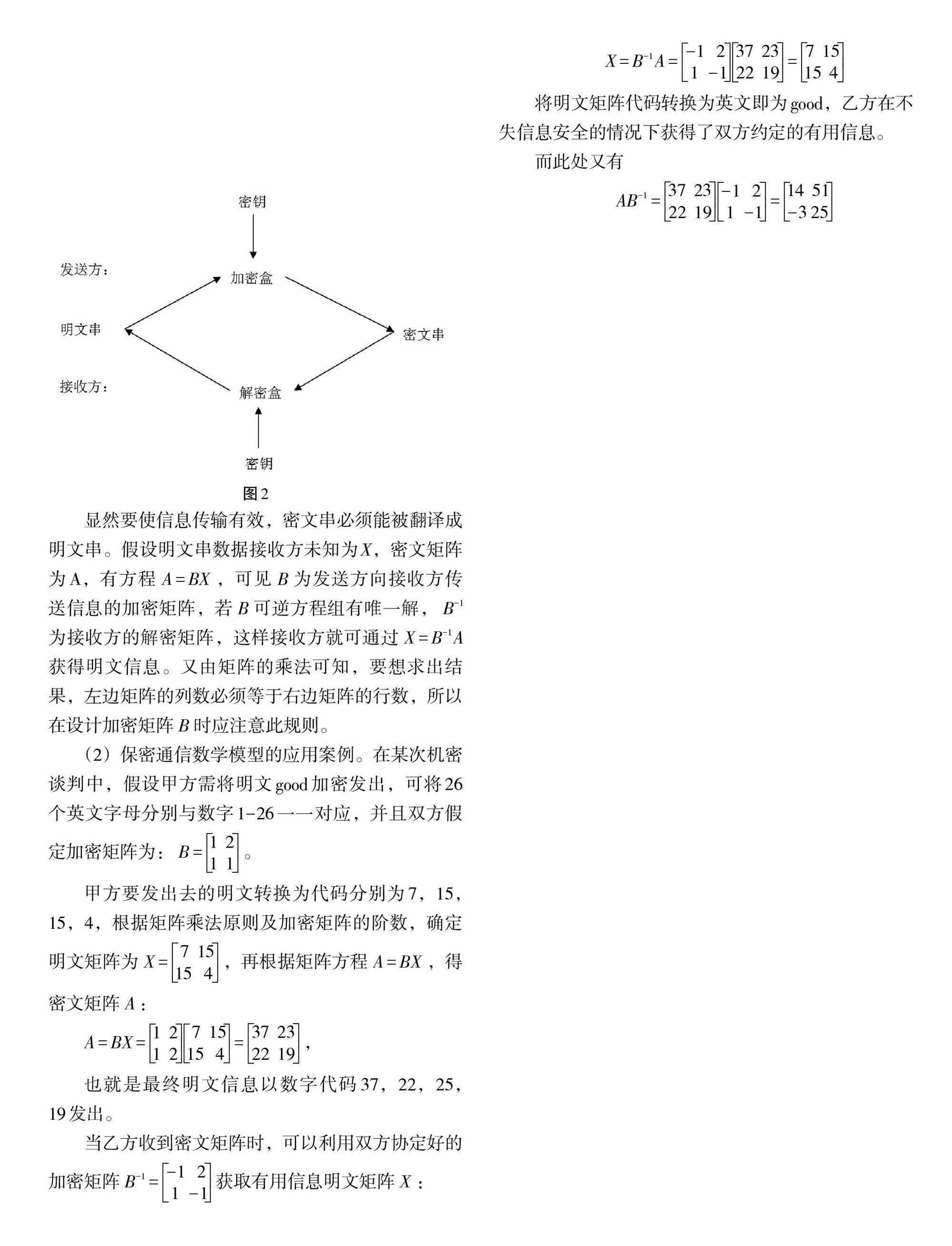
将明文矩阵代码转换为英文即为good，乙方在不失信息安全的情况下获得了双方约定的有用信息。

而此处又有

[AB-1=37  2322  19-1   2 1  -1=14  51-3 25]

此密文串无法转换成原来的明文串good，也就说明[B-1A]与[AB-1]的表达意义并不一样。

通过以上保密通信数学模型的讲解，让学生进一步巩固了矩阵乘法的运用，又学到了有关矩阵的逆的相关概念;同时有[AB-1≠AB-1]，可以让学生清晰地掌握求解矩阵方程组时要注意是左乘还是右乘，以及矩阵的乘法不满足交换律。在满足学生学习兴趣的同时，结合现代社会需求，让学生通过一个模型掌握了线性代数中多个重要的知识点。

基于培养学生知识应用能力，将数学建模思想融入线性代数教学的改革，順应“新工科”建设培养创新型、应用型高素质人才的诉求。本研究结合大学生学习心理的研究，给出了符合时代发展要求的创新型案例，旨在培养学生对数学的学习兴趣，锻炼学生理论联系实际的能力，让学生能够真正运用所学知识分析、解决现实问题，养成良好的分析问题、解决问题的习惯，使工科学生能够得心应手地运用数学知识解决自己学科领域的问题。本文中给出的案例也只是基础性的，在线性代数课程中融入数学建模思想的教学改革仍处在探索阶段，还需要更加深入的实践研究。

参考文献：

[1] 钟登华.新工科建设的内涵与行动[J].高等工程教育研究，2017，（3）：1-6.

[2] 杜允.大学生学习心理研究述评[J].南阳师范学院学报，2012，11（11）：101-103+107.

[3] 张新文，王佳.基于可逆矩阵加密技术的保密通信数学模型[J].西南师范大学学报（自然科学版），2017，42（2）：166-170.

责任编辑  陈  佩