安徽省合肥市教育局教科院 (邮编：230031)

1 深度学习的提出

深度学习的概念源于对人工神经网络的研究，是指一种主动的、批判性的、建构的和面向问题解决的学习方式，也是实现有意义学习的有效方式.深度学习在教育上的意义是指在教师的引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程.判断深度学习是否发生的五个标准为：第一，联想与结构：经验与知识的相互转化；第二，活动与体验：学生的学习机制；第三，本质与变式：对学习对象进行深度加工；第四，迁移与应用：在教学活动中模拟社会实践；第五，价值与评价：“人”的成长的隐形因素.深度学习发生的条件为：第一,学生思考和操作的学习对象，必是经过教师精心设计，具有教学意图的结构化的教学材料；第二，教学过程必须有预先设计的方案，要在有限的时空下，有计划、有序地实现丰富而复杂的教学目的；第三，要有平等、宽松、合作、安全的互动氛围[1].

2 深度学习的实践

何谓深度，从工作、认识的角度认为是触及事物本质的程度[2].

深度学习体现在深度二字上.数学教学若能引导学生用内心创造和体验的方法来学习数学;鼓励学生寻求解法，而不是记住步骤；探索模式，而不是模仿题型；形成猜想，而不是仅仅做练习题；帮助和鼓励学生按自己的想法和语言重建所学的东西；鼓励学生用学到的知识去修正和改造原有的观念和想法[3].首先我们在教学实践中采用任务具体化、推理分步化、应用具体化，使得学生的学习积极参与，获得成功的体验[4].其次又围绕数学教学促进初中生深度学习进行实践研究.

2.1 概念深剖

数学中的概念是数学的基石.数学大厦是由数学中的概念、定义、定理、公理建立的.数学中的概念是前人日积月累形成的，是前人智慧的结晶.数学概念具有抽象性、严谨性，学生在理解上有一定困难.深度学习是有意义学习，应在概念同化的基础上，达到概念的顺应.

案例1 如在上海科技出版社出版的新时代数学编写组编著的教育部审定(2012)义务教育教科书数学七年级下册第88-89页的分式及其基本性质第1课时的教学过程中是这样设计的：

问题1 (1)一块长方形木板的面积为10m2,宽为3m，则长为______m；

(2)一块长方形木板的面积为10m2,宽为am，则长为______m；

(3)一个长方形的面积为Sm2，如果它的长为am，那么它的宽为______m.

问题2 (1)有两块稻田，第一块是4公顷，每公顷收水稻10500kg；第二块是3公顷，每公顷收水稻9000kg，这两块稻田平均每公顷收水稻______kg.

(2)如果第一块是m公顷，每公顷收水稻akg；第二块那是n公顷 ，每公顷收水稻bkg，则这两块稻田平均每公顷收水稻______kg.

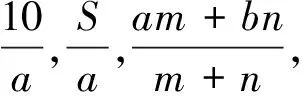
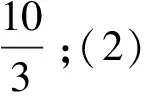
类比分数的除法算式，引出分式的概念.

下列式子中，哪些是分式？哪些是整式？

在下列所给的整式中选两个，你能组合出几个不同的分式？请都写出来.

x-2，4，2x-3，x+4.

此环节学生共写出：

2.2 探索领悟

探索的释义是多方寻求答案，解决疑问[5].

2011年版义务教育数学课程标准的课程理念要求：课程内容的选择要有利于学生体验与理解、思考与探索；学生学习除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式.教师教学要引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能、数学思想和方法，获得基本的数学活动经验.要有效地改进教与学的方式，使学生乐意并有可能投入到现实的、探索性的数学活动中去.这说明数学中的探索活动对学生的数学理解、领悟有举足轻重的价值.如

案例2 定理n边形的内角和等于(n-2)·180°(n为不小于3的整数).

探索1 由三角形出发，到四边形时从一个顶点出发可以分割成(n-2)个三角形，利用三角形内角和为已知，把未知转化为已知.如图1.

图1

探索2 由四边形的内部任取一点出发与各顶点连接可以得到四个三角形，内角和为4×180°，减去一个360°，所以四边形的内角和为(4-2)·180°，类推，过n边形的内部一点与各顶点连接所得到的n个三角形的内角和为(n-2)·180°.

探索3 由四边形的某一边上任取一点出发与不相邻的顶点连接可以得到三个三角形，内角和为3×180°，减去一个180°，所以四边形的内角和为2·180°=(4-2)·180°，类推，过n边形的内部一点与不相邻顶点连接所得到的n-2个三角形的内角和为(n-2)·180°.

探索4 由四边形的外部任取一点出发与各顶点连接可以得到三个三角形，内角和为3×180°，减去一个由该点和所对边组成的三角形的内角和为180°，所以四边形的内角和为2×360°，所以四边形的内角和为(4-2)·180°，类推，过n边形的外部一点与各顶点连接所得到的n个三角形的内角和为(n-2)·180°.

从而让学生在探索中领悟解决疑问的思想是未知转化为已知.

2.3 思维递进

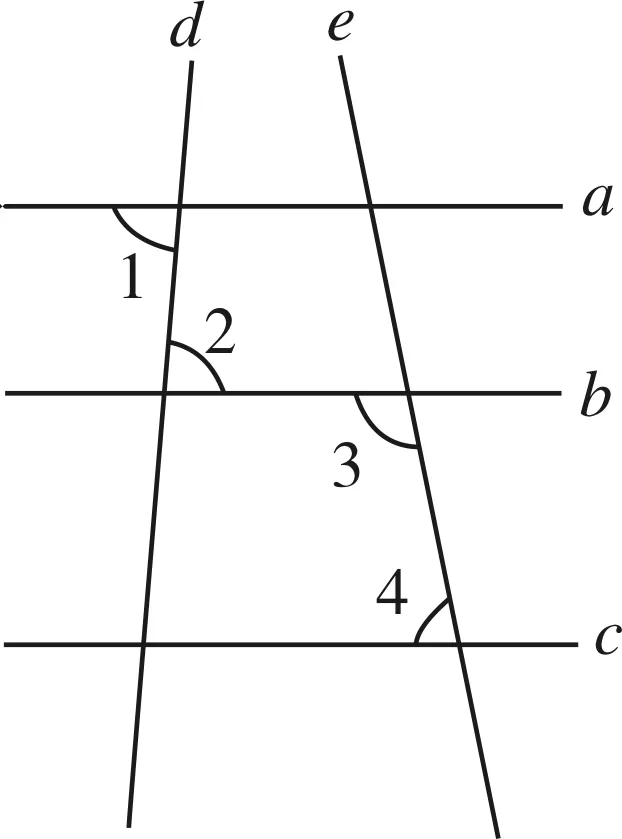
图2

深度学习是阶梯式的学习，教师根据学生的认知水平，设计由浅入深、由表及里的解题过程，能让学生的数学学习与思维不断深入.如在平行线判定方法的应用教学时，教师设计如下系列问题：

问题1 如图2所示,已知直线a、b、c、d、e，且∠1=∠2，∠3+∠4=180°，则a与c平行吗?为什么?

利用平行线判定方法可得.

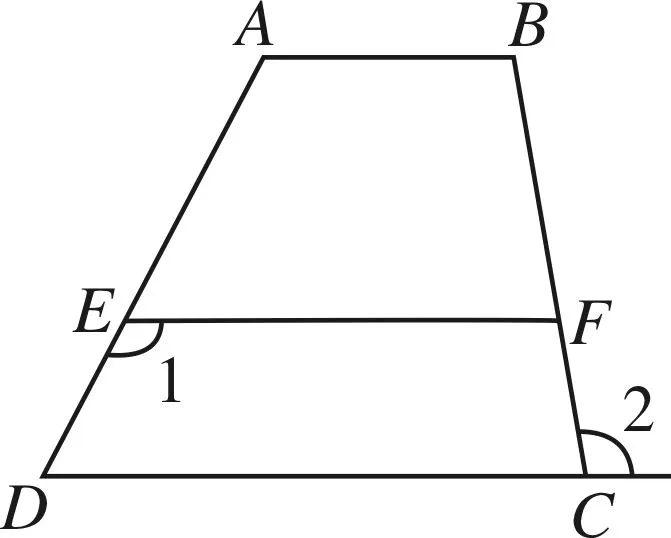
图3

问题2 如图3，如果∠1=∠A，∠2=∠B，那么直线EF∥DC吗？为什么？

利用平行线判定方法和平行的传递性可得.

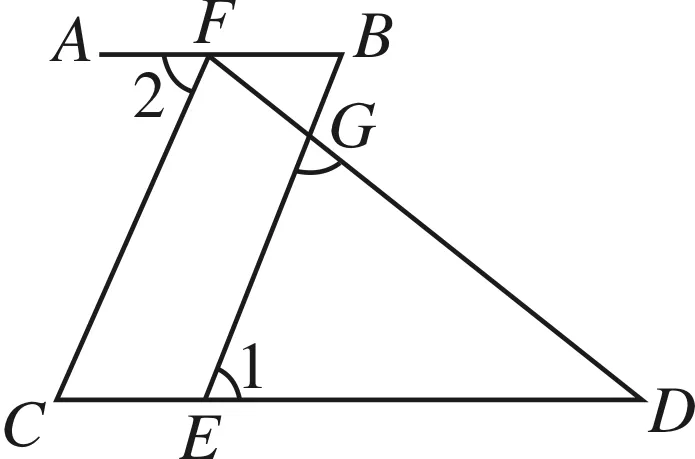
图4

问题3 如图4，∠C=∠1，∠2与∠D互余，BE⊥DF，垂足为G．求证：AB∥CD．

利用平行线判定方法、余角性质、三角形内角和定理可得.

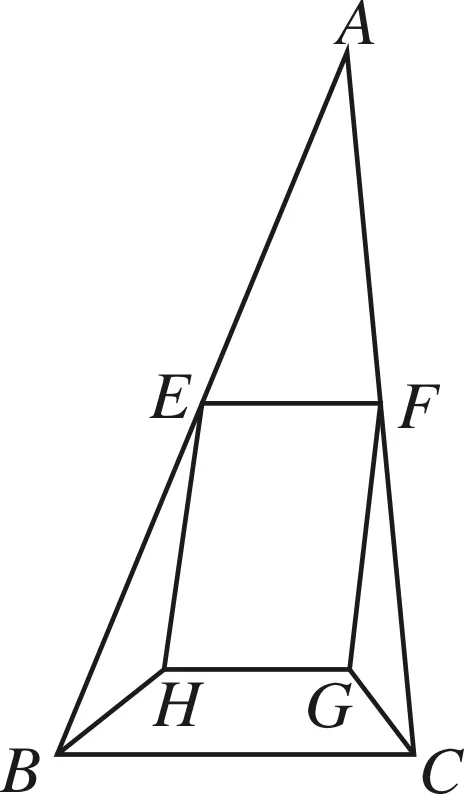
图5

问题4 如图5，已知∠BEH+∠AEF=90°，EH⊥HG，∠ABH+∠HBC=∠AEF，求证：HG∥BC.

利用平行线判定方法和垂直定义可得.

该系列问题由浅入深、由表及里，思维不断深入.

2.4 运算熟练

深度学习是主动式的学习，教师要不失时机地给学生提供主动学习的机会.而设计不同形式的运算，能激发学生主动学习的心向.如在沪科版初中数学九年级上册第119页的任意一个锐角的正(余)弦值，等于它的余角的余(正)弦值的教学中，教者采用头脑风暴的形式完成如下填空：

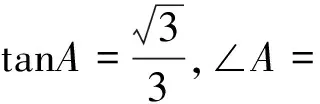
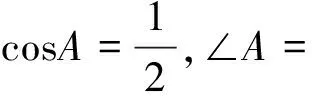
sin45°=.

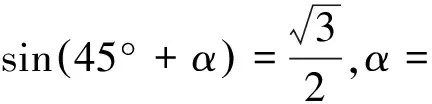
sin30°-cos60°=.

sin45°-cos45°=.

这几个式子的运算，不仅有对30°,45°,60°特殊三角函数值的回忆，也有逆向思维的训练.

接着思考：30°,45°,60°这三个角的正(余)弦值和它们余角的余(正)弦值有什么关系？从特殊到一般 归纳出“任意一个锐角的正(余)弦值，等于它的余角的余(正)弦值.”即是sinA=cosB=cos(90°-∠A)，cosA=sinB=sin(90°-∠A).

给出结论的直接应用：已知sin22°=0.3746,cos22°=0.9272，求68°的正弦、余弦的值.

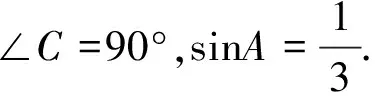
(1)求cosB的值；

(2)求sinB、tanB的值.

思考sinα、cosα、tinα之间有何关系？sinα、cosα之间有何关系？

教者在结论基本巩固的基础上，安排如下当堂练习：

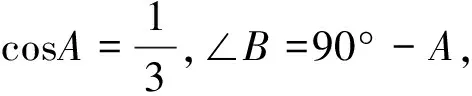
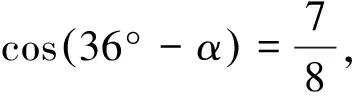
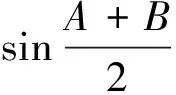
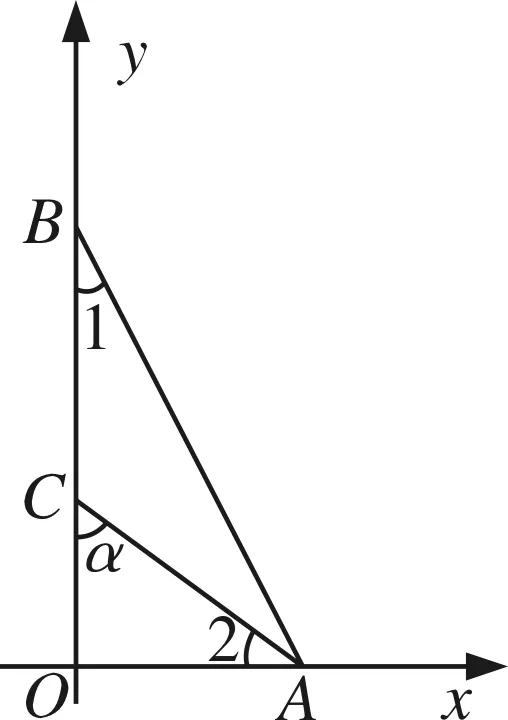
图6

5.如图6，已知两点A(2,0),B(0,4)，且∠1=∠2，则sinα=.

练习1是直接利用结论解决；练习2运用整体思想和结论解决；练习3利用三角形内角和定理和结论解决；练习4利用结论解决.

练习5的解法二因为A(2,0),B(0,4)，

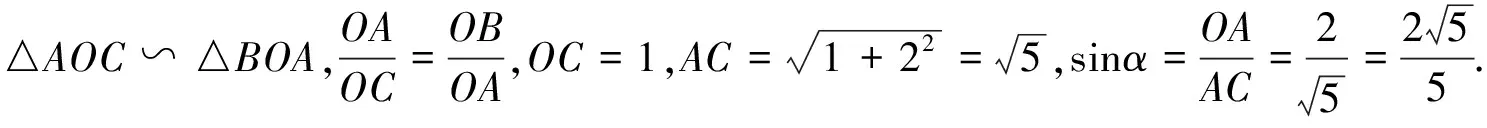
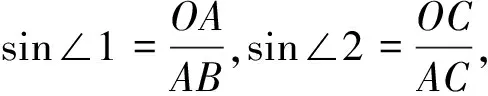
又△AOC为直角三角形，OC2+OA2=AC2，两式联立解得

本部分虽然以运算为主，但渗透方程、整体、特殊到一般的思想和发散性思维的培养.

2.5 问题变式

图7

深度学习是理解性学习，教师要对问题进行深层次加工，引导学生通过深切的体验与深入的思考，达成对问题的理解.对问题的变式就是深层次的加工，对问题变式的求解过程可以加深对问题的理解.如三角形的复习课安排如下问题：

案例3 已知：如图7，△ABC中，AB=AC,∠A=90°,BD平分∠ABC,CE⊥BD，垂足为E，求证：BD=2CE.

略证延长CE,BA相交于F，可证△CAF≅△BAD，

BD=CF，∠BCF=∠BFC=67.5°，△BCF是等腰三角形，BE⊥CE，E为CF的中点，所以BD=2CE.

变式一已知：如图7，△ABC中，AB=AC,∠A=90°,D是AC上一点，CE⊥BD，垂足为E，BD=2CE，求证：BD平分∠ABC.

略证延长CE,BA相交于F，∠BDA=∠CDE，∠DCE+∠CDE=90°,∠DCE+∠CFA=90°，可证△CAF≅△BAD，BD=CF，

CF=2CE，E是CF的中点，BE⊥CE，BD平分∠ABC.

变式二 已知：如图7，△ABC中，∠A=90°,D是AC上一点，CE⊥BD，垂足为EBD=2CE，BD平分∠ABC,求证：AB=AC.

略证延长EF=CE与BA相交于F，因为BD平分∠ABC，所以BC=BF，

∠BCF=∠BFC，∠BFC+∠FBE=90°，又∠ADB+∠FBE=90°，∠BFC=∠ADB，∠CDE+∠ECD=90°，∠CDE=∠ADB，∠ECD=∠ABE，可证△CAF≅△BAD，可得AB=AC.

变式三已知：如图7，△ABC中，AB=AC，D是AC上一点，CE⊥BD，垂足为E，BD=2CE，BD平分∠ABC,求证：∠A=90°.

略证延长EF=CE与BA相交于F，因为BD平分∠ABC，所以BC=BF，

∠BCF=∠BFC，∠BFC+∠FBE=90°，∠ACB+∠ECD+∠EBC=90°，

∠EDC=∠ACD+∠EBC，又∠EDC+∠ECD=90°，∠ECD=∠EBC，AB=AC，可证△CAF≅△BAD，可得∠FAC=∠BAC,可得∠A=90°.

图8

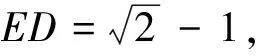
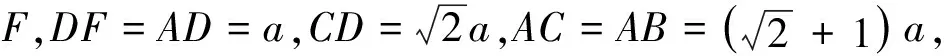
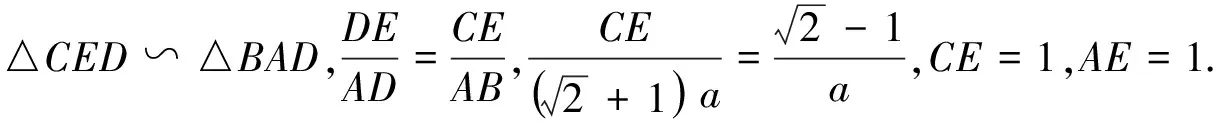
变式五已知：如图8，△ABC中，AB=AC，BD平分∠ABC交AC于D，CE⊥BD，垂足为E， 且BD=2CE，连接AE，猜想BE,CE,AE之间的关系并证明.

略解延长CE,BA相交于F，由已知可证∠A=90°，设AE=x,CE=y,BD=2y，

将一题演变成多题，而题目实质不变，让学生解答这样的题目，能随时根据变化的情况思考，从中找出它们之间的区别与联系，以及特殊与一般的关系，达到对问题的加深理解.

3 几点建议

3.1 处理好深度学习与行为主义，认知主义，人本主义，建构主义[6]的关系

深度学习源于人工神经网络的研究，按其释义和在教育上的释义，似乎涵盖了上述四种学习的理论，是否可以说深度学习是上述四种学习的上位学习？实质上，行为主义的数学教学强调教师是知识的传授者，学生是知识的接受者；教学内容要化整为零；教学目标细化.认知主义的数学教学强调教师与学生是教学的双主体；根据学生信息加工过程来考察教学活动；强调在教学中发展和培养学生的认知和元认知能力；提倡“问题解决”.人本主义的数学教学注重情感教育；构建真实的问题情境，提倡从做中学，鼓励学生自由探索；提倡课堂的创造活动；合作学习.建构主义的数学教学要求学生通过高级思维活动来学习，学习者要不断思考和对各种信息进行加工转换，基于新经验与旧经验进行综合概括去建构知识.总的来说是教师为主导的教向学生为主体的学的转变.深度学习的数学教学就是要求教师给学生提供主动的、批判性的、建构的和面向问题解决的学习素材，实现有意义学习.

3.2 处理好深度学习与面向全体的关系

初中教育属于义务教育，小学是就近、划片、免试升入初中.学生存在数学学习的差距是必然的.在这样的班级上，课堂教学中如何使学生进行深度学习呢？笔者认为，在创设情境时尽量联系生活实际，在探索问题时尽量设置台阶，在安排运算时尽量由浅入深，在进行问题变式时尽量面向全体，在进行思维训练时尽量在最近发展区内.

3.3 处理好深度学习与教师理解的关系

深度学习并不能自然发生，它需要促发条件.其中，先决条件是教师的自觉引导.深度学习中学生思考和操作的学习对象，必是经过教师精心设计、具有教学意图的结构化的教学材料；教学过程必须有预先设计的方案，要在有限的时空下，有计划、有序地实现丰富而复杂的教学目的.因此，教学中教师必须理解深度学习发生的标准和条件，深刻理解教材中实施深度学习的素材，设计好进行深度学习的方案，有条不紊地组织学生探索新知识的活动.

总之，教师对教学内容的深度理解、学生认知情况的深度分析是进行深度学习的出发点，恰当且有深度的学习目标是导航，好的引导问题、有吸引力的学习活动是深度学习的核心和关键，精准、及时的评估是深度学习的保障.

本文特别致谢合肥市第六十八中学数学组孙自海、韩芬芬、钱雪、杨菊、王春苗老师提供的教学实例.