电导率线性变化直流电测深三维有限单元法正演模拟
2019-10-25欧东新闫凯暄
欧东新,王 超,闫凯暄,冯 欢
(1.桂林理工大学 a.广西隐伏金属矿产勘查重点实验室;b.地球科学学院,广西 桂林 541006;2.中国有色桂林矿产地质研究院有限公司,广西 桂林 541004)
0 引 言
三维直流电测深的正演是进行复杂地电模型勘探资料反演的基础,主要采用有限单元法、边界单元法、积分方程法、有限差分法等方法。Xu等[1]利用边界单元法进行了起伏地形三维电阻率法的正演模拟。Zhang等[2]利用共轭梯度法进行了三维电阻率法的有限差分正演模拟和反演。底青云等[3]利用积分方程法进行了三维电阻率成像的研究。 Li等[4]利用不完全共轭梯度法进行了有限单元法三维直流电阻率法的正演模拟,并与有限差分法对比,得出当模型电阻率差异较大时,有限单元法计算精度优于有限差分法的结论。黄俊革[5]用有限单元法对电导率、极化率分块均匀的地下介质进行了正反演研究。吴小平等[6]采用对称超松弛预条件共轭梯度(SSOR-PCG)迭代算法求解三维电阻率有限元法形成的大型线性方程组。 Rücker等[7]进行了三维电阻率有限单元法正演,采用异常电位法计算,着重于网格剖分、正常电位的计算以及直接法与迭代法解方程的对比;在计算起伏地形正常电位时,在电源点附近局部加密网格,采用二次形函数对电位插值。吕玉增[8]采用有限单元法进行了地-井、井-地激发极化法三维快速正反演研究,利用改进的稀疏矩阵MSR(modified sparse row)存储方法存储系数矩阵, 采用SSOR-PCG迭代算法求解大型线性方程组。 任政勇等[9]利用非结构化网格进行了三维直流电阻率有限单元法正演模拟。 李长伟[10]采用Krylov子空间预条件共轭梯度法(PCG)解三维电阻率有限元法形成的大型线性方程组。
以上直流电测深三维正演都是电导率分块均匀的,而野外的地电分布一般是连续变化的,尤其是地下水的电导率与矿化度成正比,因此有必要研究电性参数连续变化的正演模拟方法。阮百尧等进行了电导率线性变化的二维地电断面电阻率法有限单元法正演模拟[11], 并进行了水平大地电导率线性变化电阻率法三维有限单元法正演[12],采用了非齐次边界条件、异常电位法进行模拟,但是没有提到用何种方法进行线性方程组的求解,根据文中计算时间较长推测,应该是采用直接解法。刘海飞等[13]进行了起伏地形电导率连续变化的三维激电数据有限元数值模拟,采用非齐次边界条件,四面体单元剖分,单元内电导率线性变化,由于采用总电位法,在电源点附近误差较大。刘海飞等[14]利用异常电位法进行了电导率线性变化的五极纵轴激电测深三维有限元正演模拟,仍然采用非齐次边界条件。
本文采用与文献[12]类似的方法进行电导率线性变化的直流电测深三维正演模拟,也利用六面体单元剖分模拟水平大地三维地电结构;电导率和电位在单元内线性变化;采用异常电位法进行正演,推导出齐次边界条件下有限单元法系数矩阵,令总电位为正常电位和异常电位之和。有限元法计算的是异常电位,与点源水平均匀大地的正常电位相加即可获得总电位。
与文献[12]不同之处在于,本文采用齐次边界条件,这样有限单元法的系数矩阵不会随着电源点位置的改变而不同,在多个电极的情况下特别有利。如果采用直接法(如乔累斯基分解法)求解包含多个不同右端项的线性方程组,一次分解多次回代,可以节省大量的时间;如果采用迭代法求解,也有方法能快速求解这种线性方程组[10]。此外,还采用林绍忠[15]改进的SSOR PCG迭代算法求解线性方程组,当网格节点较多时,迭代法比直接法计算速度要快[7]。有限单元法计算结果与一维水平层状电导率线性变化模型滤波算法对比,相对均方差小于0.38%。对二维垂直不连续分界面模型、均匀大地中的三维低阻体模型也进行了电阻率测深正演计算,验证了本文方法的有效性。
1 三维模型网格剖分
如图1所示, 计算区域为大的六面体, 建立直角坐标系,x、y、z在3个方向进行剖分就可以形成结构化六面体单元,与非结构化单元相比, 网格生成简单, 由于单元排列有规律, 在计算网格节点编号、 有限元存储矩阵参数等方面非常省时。

图1 六面体单元网格剖分示意图Fig.1 Skech map of hexahedron mesh
2 变分问题
由文献[16]得到三维点源电场的异常电位法变分公式
(1)
其中:u为异常电位;σ为电导率;σ′=σ-σ0为异常电导率;σ0为背景电导率;u0为正常电位(即大地电导率全部为σ0的电位);Ω为有限单元法计算区域。 本文采用齐次边界条件, 即在无穷远处异常电位为零, 因此式(1)省略了无穷远边界的积分。
3 有限单元法系数矩阵
对式(1)积分采用六面体单元离散化, 六面体母单元、 子单元如图2所示, 插值形函数如式(2)所示[17]。
Ni=(-1)1+ξi+ηi+ζi(ξ+ξi-1)(η+ηi-1)(ζ+ζi-1),i=1,2,…,8。
(2)
单元内电导率、 电位利用线性变化形函数插值
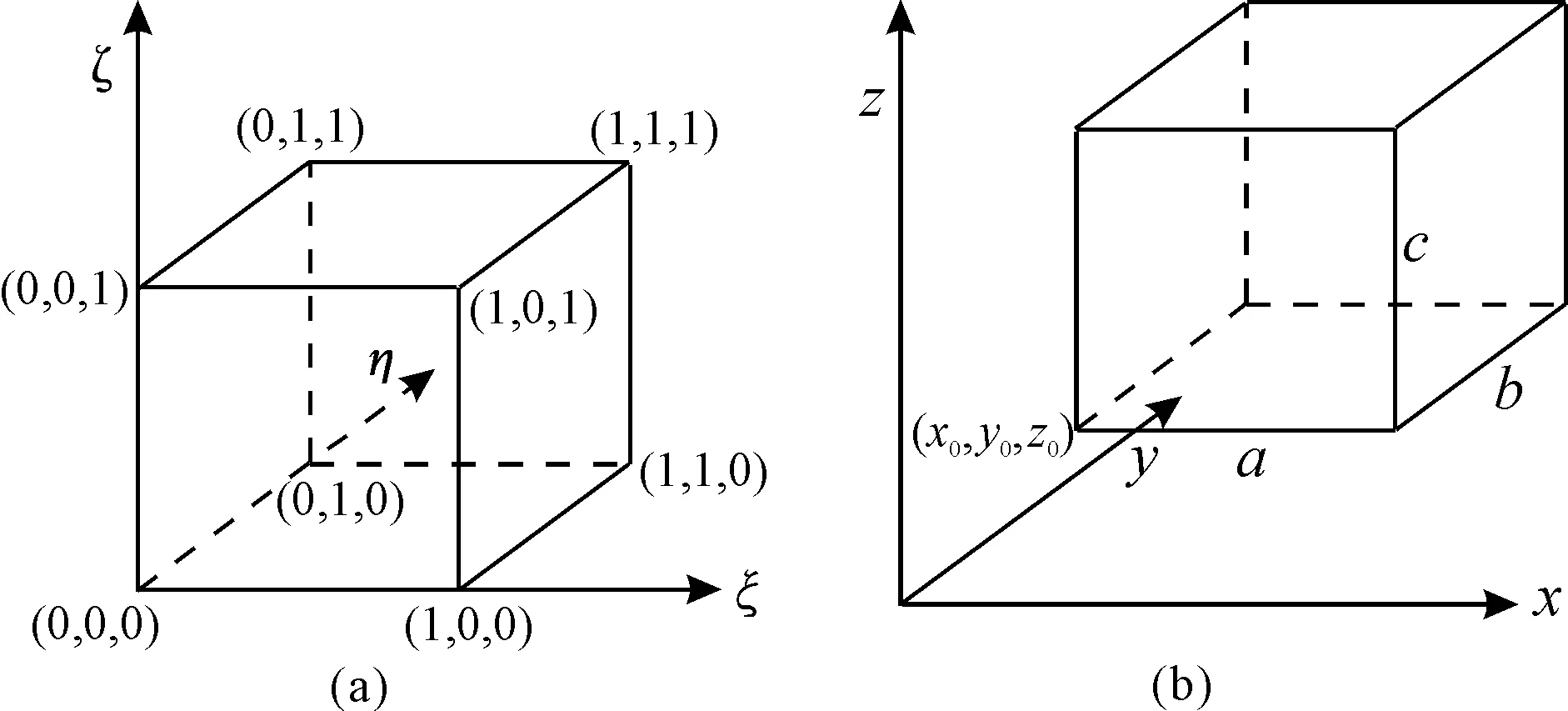
图2 六面体母单元(a)和子单元(b)Fig.2 Parent element(a) and subelements(b) of hexahedron
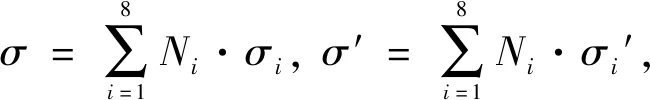
(3)
子单元的坐标也线性变化
(4)
将式(1)积分离散为各个六面体单元积分之和
(5)
利用式(3)对单元积分进行插值,得
(6)
其中:ke与ke′为8×8单元系数矩阵;ue为8个元素的单元异常电位列向量;u0e为8个元素的单元正常电位列向量。
由于本文母子单元都是长方体,所以有
x=x0+aξ,y=y0+bη,z=z0+cζ,
(7)
其中:a、b、c为子单元在x、y、z三个方向的边长。由式(7)可得
dv=dxdydz=abcdξdηdζ。
(8)
由文献[16]可得
(9)
其中:J为雅可比变换矩阵。J中的元素可以由式(4)分别对ξ、η、ζ求导获得。

(10)
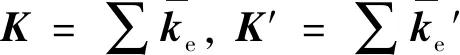
令式(10)变分为零获得如下线性方程组
(11)
求解式(11)获得异常电位后与正常电位相加即可获得总电位,从而求得视电阻率。本文推导了六面体剖分,单元内电导率线性变化的单元系数矩阵ke和ke′:
(12)
其中,kij为8×8单元矩阵ke或ke′的元素;Aij为8×3矩阵;当S为单元8个节点的电导率向量时, 式(12)计算的是ke的元素;当S为异常电导率向量时, 式(12)计算的是ke′的元素;α=ab/c;β=ac/b;γ=bc/a;a、b、c为子单元在x、y、z三个方向的长度。 限于篇幅, 36个Aij的具体形式未在此列出。
5 线性方程组求解及程序实现
式(11)方程组的系数矩阵为大规模稀疏矩阵,特别适合用迭代法求解,Rücker等[7]对直接法和迭代法进行了对比,发现在节点数较少时采用直接法计算速度较快,节点数较多时采用迭代法计算速度更快,而三维模拟节点数一般都在几万以上,所以采用迭代法较好。本文采用林绍忠[15]改进的SSOR PCG公式编写了线性方程组的迭代求解程序。将此程序应用于笔者以前的正演模拟中[18-19],在满足一定精度的条件下,与直接解法相比,计算速度极大提高。
林绍忠改进的SSOR PCG法如下,设有线性方程组
Ax=b,
(13)
其中:A为对称正定矩阵, SSOR法的分裂预处理矩阵为
M=(2-ω)-1(D/ω+L)(D/ω)-1(D/ω+L)T,
(14)
其中:D为A的对角阵;L为A的下三角阵; 0<ω<2为松弛因子。
令
(15)
则
(16)
有改进的SSOR PCG迭代格式:
(17)
其中:W是方阵;W-T为W的转置矩阵的逆阵;V为对角阵;g,h,y,d,z,x,b为列向量。
迭代式(17)中需要计算W-1(zk-Vdk)和W-Tzk+1,在实际计算中不需计算逆阵,而是利用SSOR理论迭代一次就可获得,以下推导具体的计算公式。
由式(14)和式(15)可得
M=WV-1WT,
(18)
M-1=W-TVW-1。
(19)
对式(19)两边左乘(W-TV)-1可得
W-1=V-1WTM-1,
(20)
因此,W-1与任意列向量b的乘积为
W-1b=V-1WTM-1b。
(21)
根据SSOR理论[20],对于线性方程组(13)有
M-1b=xk+1-Bxk,
(22)
其中:B=(D/ω+U)-1[(1/ω-1)D-L](D/ω+L)-1[(1/ω-1)D-U];U为L的转置矩阵,即上三角阵。 只要令xk=0, 按照SSOR公式迭代一次算出xk+1即M-1b。 因此只需令b=(zk-Vdk), 先用SSOR迭代一次算出M-1(zk-Vdk), 然后利用式(21)即可获得W-1(zk-Vdk)。
下面推导W-Tzk+1的计算公式,式(19)两边右乘(VW-1)-1可得:
W-T=M-1WV-1,
(23)
W-Tzk+1=M-1WV-1zk+1。
(24)
同样进行一次SSOR迭代就能求出式(24)。
为了减少存储占用, 对系数矩阵进行CSR(行压缩的稀疏存储)存储,只存非零元素。 由于采用结构化六面体网格,网格编号有规律, CSR的压缩矩阵指示参数的计算非常快速, 47 068个节点用时10-2s以下, 而用非结构化网格方法计算压缩矩阵指示参数用时30 s。 根据Rücker等[7]的研究, 只要迭代法的残差小于10-6, 求解精度就可以满足勘探的要求, 本文也采用这个精度标准。 由于相邻电极供电时的电位分布特征接近, 第1个电极供电的初始解设为0, 此后所有电极的初始解采用上一个电极供电所计算出来的电位平移到当前电极供电时的相应节点位置上作为初始解, 这样求解的迭代次数能减小很多。 例如对模型2进行21个电极的高密度α装置的视电阻率测深数据正演, 192 892个节点, 第1个电极供电时, 电位初始值设为0,迭代次数为130次, 而其他电极采用上一个电极供电所计算出来的电位平移到当前电极供电时的相应节点位置上作为初始解, 迭代次数最多为84次, 最少为23次, 平均为34次。
由于每个电极供电都可独立计算,所以可以采用并行方法。本文采用PGI Fortran 编程,利用OpenMP 编译指令对程序进行并行化,在双核2.7 GHz笔记本上进行计算,采用并行指令的计算速度基本为串行的2倍。
5 算 例
5.1 一维水平层状电导率线性变化模型(模型1)
首先利用一维水平层状电导率线性变化模型(模型1, 图3),对称四极测深数据来检验本文方法的准确性。模型1为3层模型,第1层厚度5 m,电阻率为10 Ωm(电导率为0.1 S/m); 第2层厚度5 m, 电导率从0.1 S/m线性变化到0.01 S/m(电阻率为100 Ωm)。本文用文献[21]水平层状大地的计算方法来模拟电导率线性变化的模型,将第2层过渡层用多个均匀薄层来近似,用120个系数[22]的滤波算法进行计算。编制程序对过渡层不断细分,直到前后两次细分模型的视电阻率相对均方差小于0.001%时终止分层,所得结果作为电导率线性变化模型的理论值。
对模型1的有限单元法网格剖分如表1所示。
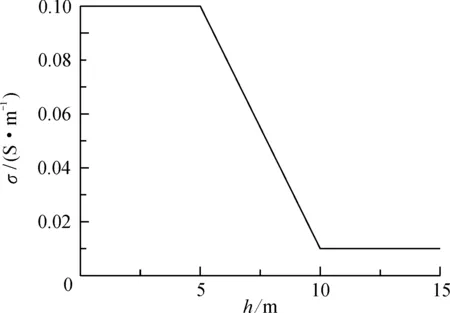
图3 一维水平层状电导率线性变化模型(模型1)Fig.3 1D layered model with linear variable conductivity (Model 1)

坐标节点值/mx-10230,-5110,-2550,-1270,-630,-310,-150,-70,-30,-10,0,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200,210,230,270,350,510,830,1470,2750,5310,10430y-10230,-5110,-2550,-1270,-630,-310,-150,-70,-30,-10,0,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200,210,230,270,350,510,830,1470,2750,5310,10430z0,0.5,1,2,3,4,5,10,15,20,25,30,35,40,45,50,60,75,100,150,200,300,450,750,1300,2500,4500,8500
节点个数为41×41×28=47 068。 线性方程组系数矩阵的上三角部分CSR方式存储元素为623 815个。 在x方向布置测线, 共21个电极, 电极距10 m,计算了α装置的视电阻率测深数据。21个电极的高密度测深有限元计算用时为12.5 s。阮百尧等[12]的方法计算一条测深曲线用时1 825 s,如果只是为了计算一条测深曲线,就可以利用互换定理,将电源点放在M、N电极,而测量点放在A、B电极,这样利用乔累斯基分解就只需对方程组系数矩阵进行一次分解,而回代的时间很少,因此1 825 s基本上是解一次线性方程组的时间。为了对比直接法和迭代法在三维电测深正演模拟中的效率,采用表1中的网格参数和21个电极分别用直接法(乔累斯基分解法)和本文迭代法对模型1进行了α装置高密度正演计算。本文迭代法所用时间12.5 s, 而直接法用时110.6 s。对于更多节点的模型也进行了计算,随着节点数的增加,直接法用时急剧增加,而迭代法用时增加相对要慢一些。因此可以看出,对于三维模型,在节点数巨大的情况,迭代法比直接法快得多,这与文献[7]的结论相同。此外还要注意到本文采用的是齐次边界条件,有限单元法的系数矩阵不会随着电源点位置不同而不同,因此直接法只用一次分解,其他电源点的计算只需回代即可。而阮百尧等[12]采用的是非齐次边界条件,这样每个电源点形成的线性方程组都要重新分解,用时将会是巨大的。
理论及有限元视电阻率数据如表2所示。 理论值1个极距只计算1个值, 而本文有限元采用高密度方式采集数据, 每个极距有多个数据, 表2中给出了最小值和最大值, 以及它们与理论值的相对均方差。 在不同极距下,本文有限元计算值与理论值的相对均方差均小于0.38%。
正如滤波算法一样,如果用电导率分块均匀的有限单元法程序来模拟模型1中电导率线性变化的地电模型,需要剖分得更密才行,而从表1中z方向节点坐标可知,本文方法只用2个节点就能模拟电导率线性变化地层。
模型1理论及有限元视电阻率测深曲线如图4所示,“+”为本文有限元计算值(FEM)(表2中最小值),可见计算值与理论值拟合较好。

表2 模型1的理论及有限单元法视电阻率

图4 模型1理论及有限单元法视电阻率测深曲线Fig.4 Apparent resistivity sounding curves of theory and FEM of Model 1
5.2 垂直不连续分界面模型(模型2)
本文方法也可以模拟电导率分块均匀的地电模型,只要令单元8个节点的电导率相同即可。利用2D垂直不连续分界面模型(模型2,图5)测试本文程序对横向电性突变的计算精度。分界面左边为100 Ωm,右边为200 Ωm。垂直于分界面布置一条100 m长的测线,21个电极,电极距5 m,界面位于50 m处。利用镜像法计算高密度α装置视电阻率解析解。本文异常电位有限单元法模型的背景电阻率取分界面两侧的平均值150 Ωm,网格x、y方向节点数为83,z方向节点数为28,总节点数为192 892,电极间插入2个节点,计算用时49.56 s。有限单元法视电阻率与解析解的相对均方差为0.058%,最大相对误差为1.996%,出现在垂直分界面附近。
图6为有限元计算的对称四极剖面与理论值对比,AO为7.5 m,MN为5 m。理论对称四极视电阻率剖面曲线(实线)在从高阻体进入低阻体前会先有个小的下降再上升,然后再下降;从高阻体进入低阻体后,视电阻率有小的上升, 然后又较快地减少到低阻体的电阻率值。这些视电阻率的曲线特征与程志平[21]的垂直分界面的对称四极剖面曲线特征基本类似,但也有所不同。不同之处在于本文的测量电极MN为5 m,而文献[21]的MN为0。因此,文献[21]的曲线在垂直界面处突变,而本文理论曲线在界面处不是突变的。
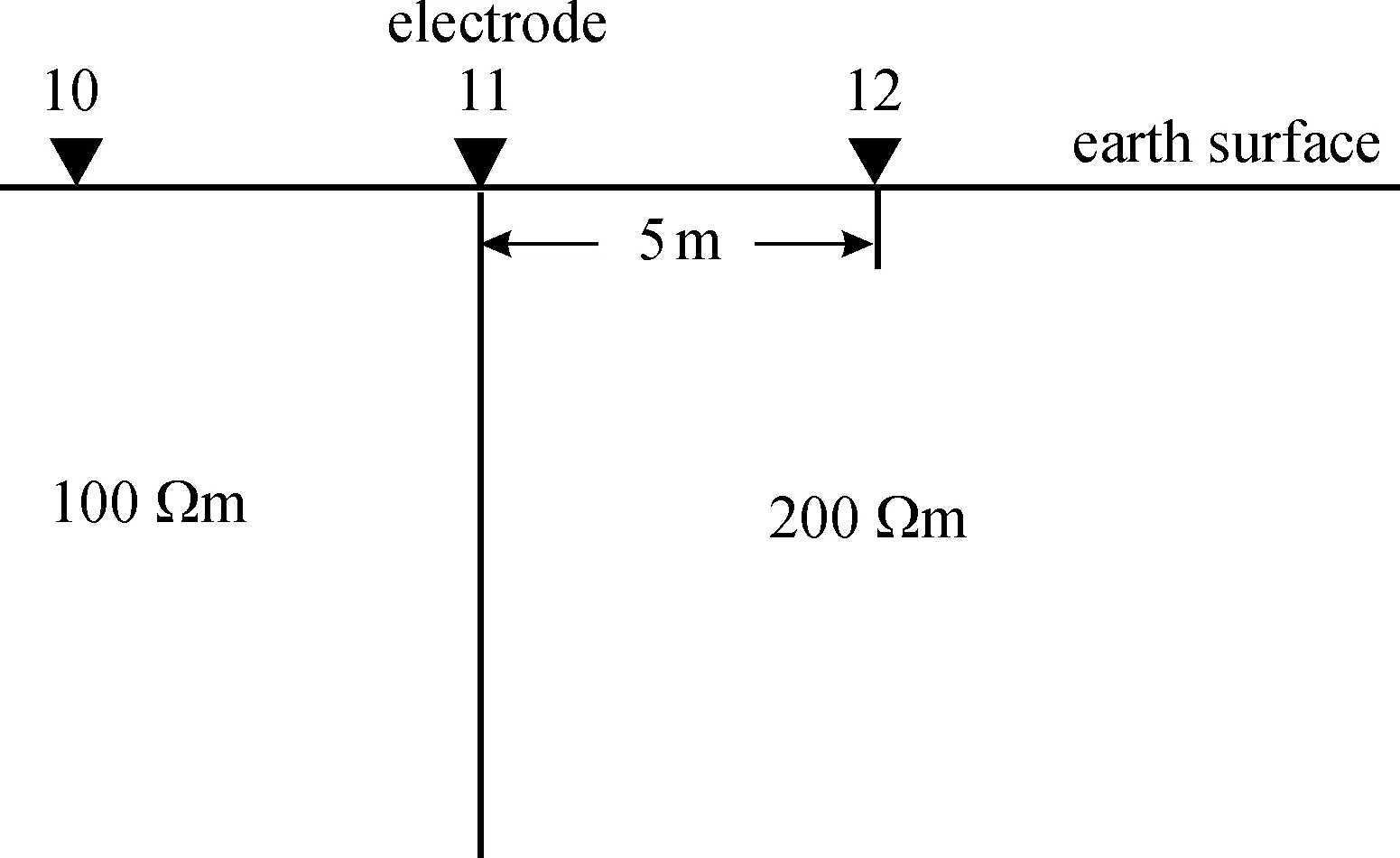
图5 2D垂直不连续分界面模型(模型2)Fig.5 2D vertical uncontinue interface model (Model 2)

图6 模型2有限元计算的对称四极剖面与理论值对比(AO=7.5 m, MN=5 m)Fig.6 Apparent resistivity curves of schlumberger array of theory and FEM of Model 2
从图6中可见,有限元计算的对称四极剖面视电阻率与理论曲线拟合较好,只在分界面附近(50 m处)有两个点误差较大(最大相对误差为1.996%)。分析误差大的原因是,在分界面附近线性变化的插值函数难以拟合电位的剧烈变化。图7、图8分别为模型2理论及本文有限单元法α装置视电阻率断面图,它们都很好地反映垂直分界面的形态,等值线图的形态也非常接近。
5.3 均匀大地中三维异常体模型(模型3)
模型3为在均匀大地中有一个10 m×10 m的低阻立方体,电阻率为10 Ωm, 顶面埋深为20 m, 围岩电阻率为200 Ωm, 在低阻体外有5 m厚的过渡区, 电导率从0.1 S/m线性变化到0.005 S/m。 布置10条测线, 线距10 m, 每条测线21个电极, 电极距10 m。 图9为模型3的侧视图, 图10为测线布置图。 有限单元法网格节点为97 468个, 电极间插入一个节点。 210个电极计算用时74.33 s, 平均每个电极解方程用时0.35 s, 迭代10次左右, 这也反映了对于均匀大地中异常体简单模型的正演计算速度较快, 因为相邻电极的电位较为接近。

图7 模型2理论α装置视电阻率断面图Fig.7 Theory apparent resistivities section of α array of Model 2

图8 模型2有限单元法α装置视电阻率断面图Fig.8 FEM apparent resistivity section of α array of Model 2

图9 模型3侧视图Fig.9 Side view of Model 3

图10 模型3俯视及测线示意图Fig.10 Vertical view of Model 3 and survey lines
有限单元法计算的各条测线视电阻率断面图如图11所示,不同极距AO的视电阻率平面等值线图如图12所示,本文有限单元法所计算的视电阻率断面图和平面等值线图能较好地反映三维低阻体的位置及形态特征。
6 结 论
(1)通过一维、二维及三维模型的正演计算,验证了本文齐次边界条件下,电导率线性变化直流电测深三维有限单元法正演模拟方法的准确性及有效性。
(2)采用改进SSOR PCG迭代算法解线性方程组与直接解法相比,能极大提高计算速度。
(3)用OpenMP 进行并行计算,并且采用相邻电极供电所计算出来的电位作为当前电极供电时的初始解,能极大减小求解的迭代次数,提高计算速度。
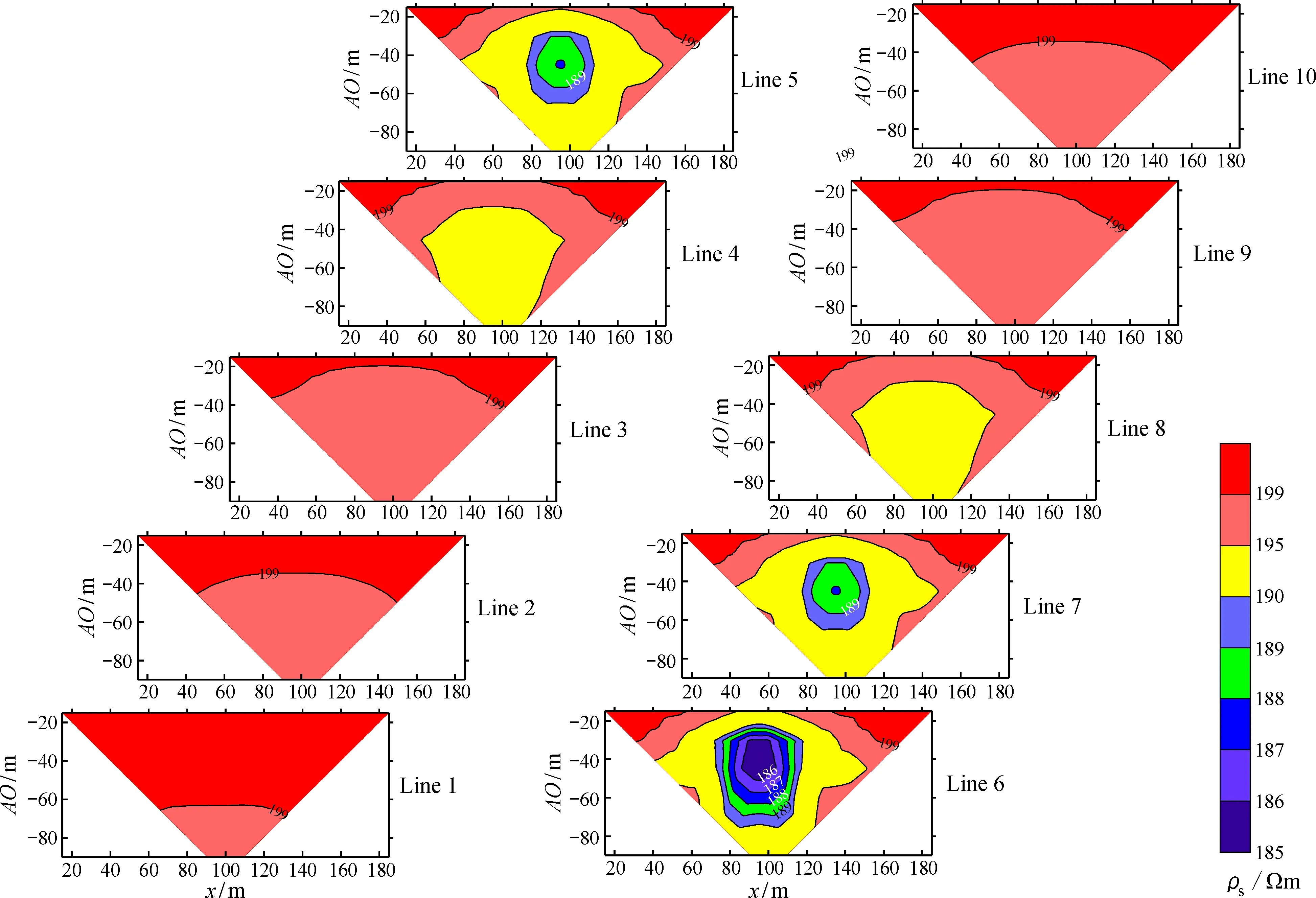
图11 模型3有限单元法α装置视电阻率断面图Fig.11 FEM apparent resistivity sections of Model 3

图12 模型3有限单元法α装置视电阻率平面等值线图Fig.12 FEM apparent resistivity plane equivalence maps of Model 3
