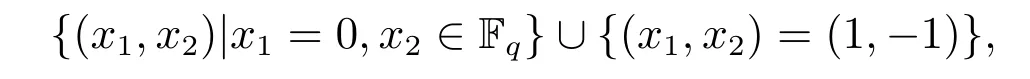由两个多项式确定的代数簇上的有理点
2019-10-24高伟黄华曹炜
高伟,黄华,曹炜
(宁波大学数学与统计学院,浙江 宁波 315211)
1 引言
本文用 N和 N0分别表示正整数集与非负整数集.设 Fq是q元有限域,其中q=pr,p为素数,r∈N.用表示由 Fq中非零元构成的乘法群.设n,t∈N,fi(X)(i=1,···,t)为 Fq上的n元多项式,V表示由多项式组f1(X),···,ft(X)所确定的代数簇.令

即Nq(V)表示代数簇V中Fq-有理点的个数;特别地,如果V由单个多项式f(X)所确定(即t=1),则记Nq(f):=Nq(V).计算Nq(V)是有限域研究 (参见文献[1-8])中的重要课题,但通常也是困难的.
文献[3]考虑了由如下单个多项式所确定的代数簇

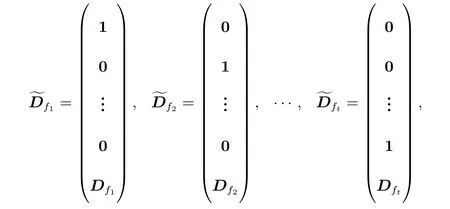
其中 0 定理 1.1[3]设f为形如 (1)的多项式.若Df是列满秩的且其最大不变因子与q−1互素,则有 本文将研究由两个多项式所确定的代数簇.下面将总是用W表示由下面两个Fq上的多项式所确定的代数簇 当W的增广次数矩阵的最大不变因子与q−1互素时,将给出代数簇W上Fq-有理点个数的具体表达式. 定义 2.2设M∈Zn×n是整数阵.若M的行列式为±1,则称M是幺模的.整数环Z上所有n阶幺模阵关于矩阵乘法构成群,用GLn(Z)表示. 设矩阵A∈Zn×m的秩为s,则存在U∈GLn(Z)和V∈GLm(Z)使得 记对角元λi:=λii,则有:(1)λi>0,λi|λi+1,其中i=1,···,s−1,λs>0;(2)λ1···λi等于A的所有i×i阶子行列式的最大公因子,其中i=1,···,s.矩阵 (λij)n×m称作A的Smith标准形,其中对角元λi(1≤i≤s)称作A的第i个不变因子. 如上节所述,设代数簇V由 Fq上的n元多项式组f1(X),···,ft(X)所确定,并记 其中 1:=(1,···,1),0:=(0,···,0),即fi的前t行除了第i行的元素全为 1,其它行均为零行向量.定义V的增广次数矩阵为V=(f1,···,Dft),并设V∈Z(n+t)×m. 用σ(k)和s(k)分别表示 (k1,···,km)和 (l1,···,ln+t)中的非零元的个数.即 文献[1]利用高斯和证明了以下引理. 引理 2.1[1]设V∈Z(n+t)×m,其中m≤n+t.设V的 Smith标准形的对角元为λ1,···,λm,其中λi|λi+1,i=1,···,m−1,λm>0.若 gcd(λm,q−1)=1,则有R={0,q−1}且 设代数簇W由多项式组(2)所确定,则W的增广次数矩阵为.假设W的最大不变因子λ满足(λ,q−1)=1.令n=max{n2,n4}及R={0,q−1}.由引理2.1知, 下面分(a)-(d)四种情形进行讨论: (a)k=0,l=0.此时显然有Nq(k=0,l=0)=qn. (b)k0,l=0.设mj−1 为方便计,定义m1−1=0,m2−1=m1.因而有 (c)k=00.若mj−1 (d)k0,l0.对固定的k′≥1 和l′≥1,σ(v) 的取值可从 2 到k′+l′.注意到n1 (i)当 0 沿用上面讨论中的定义与记号,本文的主要定理可叙述如下: 定理 3.1设代数簇W由多项式组(2)所确定.设W的最大不变因子与q−1互素.若n1,n2,n3,n4按大小顺序排列属dj(1≤j≤3)情形,则W上Fq-有理点的个数为 最后举例说明如何应用定理3.1. 设代数簇W由Fq上的两个多项式 由定理3.1知,Nq(W)=q+1.另一方面,由因式分解易知方程组g1(X)=g2(X)=0的解集为 亦可得Nq(W)=q+1.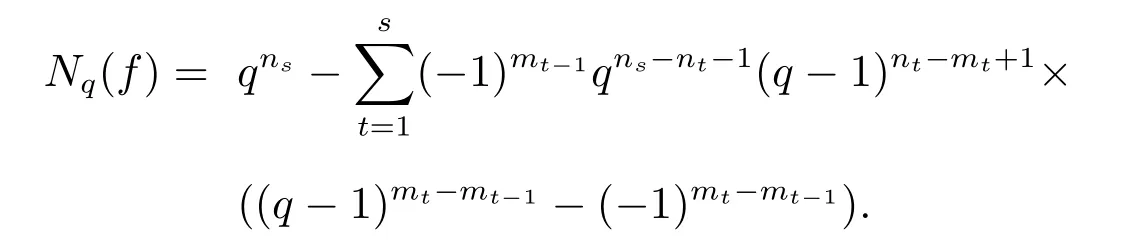
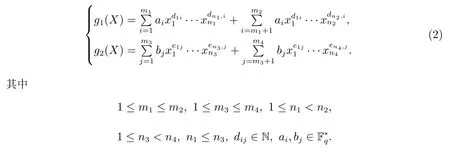
2 次数矩阵及其不变因子
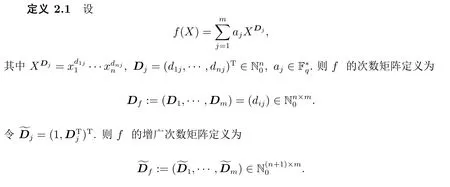

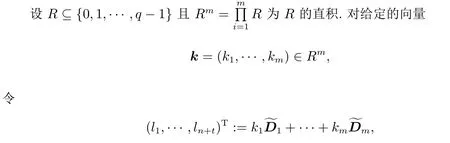
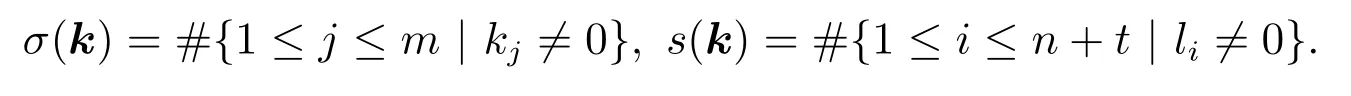

3 主要结论