New Optical Soliton Solutions of Nolinear Evolution Equation Describing Nonlinear Dispersion
2019-10-16SaudOwyedAbdouAbdelHaleemAbdelAtyandSahaRayDepartmentofMathematicsCollegeofSciencesUniversityofBishaBisha69BoxSaudiArabia
Saud Owyed,M.A.Abdou,Abdel-Haleem Abdel-Aty,and S.Saha RayDepartment of Mathematics,College of Sciences,University of Bisha,Bisha 69,P.O.Box ,Saudi Arabia
2Department of Physics,College of Sciences,University of Bisha,Bisha 61922,P.O.Box 344,Saudi Arabia
3Physics Department,Faculty of Sciences,Al-Azhar University,71524 Assiut,Egypt
4Department of Mathematics,National Institute of Technology,Rourkela,769008,Odisha,India
(Received March 17,2019;revised manuscript received June 7,2019)
AbstractIn this work,we examine two algorithm schemes,namely,Kudryashov expansion and Auxiliary equation method for obtaining new optical soliton solutions of the discrete electrical lattice models in nonlinear scheme(Salerno equation).Our solutions obtained here are include the hyperbolic,rational,and trigonometric functions.Our two used methods are proved to be effective and powerful methods in obtaining the exact solutions of nonlinear evolution equations(NLEEs).
Key words:discrete electrical lattice,generalized Kudryashov expansion method,auxiliary equation method,exact solutions
1 Introduction
Very recently,the Non-Linear Evolution Equations(NLEEs)are used to model and mathematically describe various problems in many of the research areas such as,solid state and plasma physics,optical fibers,chemical kinematics.Nonlinear electrical transmission lines which represents one of the important examples in field of physics and communications[1−12]is the one which draws our attention.
The methods used in this paper to find the solution of the NLEE’s equation are generalized Kudryashov expansion method(GKEM)and extended auxiliary equation method(EAEM).Kudryashov method is introduced in 1988 by Kudryashov to find the exact solutions of nonlinear differential equations.[13−15]Also,Kudryashov introduced a modified version of his method in 2012 with more effective performance.[16]Several authors presented new versions of Kudryashov method,where the generalized Kudryashov method introduced in many papers.[17−19]Moreover,extensions and modified versions of this method are presented in other papers.[20−25]The second method used in this paper in finding the solution of our differential equation is Auxiliary equation method. The method was invented previously as an extension of an old method as method for solving the partial differential equations.[26−29]Recently,several improvements and modifications are added to AEM,for example,a new version of an auxiliary equation method is prposed by introducing a new first-order nonlinear ordinary differential equation with six-degree nonlinear term and its solutions to construct exact traveling wave solutions of NLPDEs in a unified way.[30−31]
Since long times ago the NLEEs have great importance in the description of the physical systems.Many examples of these equations are derived like sine-Gordon equation,sinh-Gordon,the Benney-Newell equation,the Kortewegde Vries equation,the modified Korteweg-de Vries equation,Burgers and Bossingues equations.[32]NLEEs are frequently used to describe many problems of protein chemistry,chemically reactive materials,in ecology most population models,in physics the heat flow and the wave propagation phenomena,quantum mechanics,fluid mechanics,plasma physics,propagation of shallow water waves,optical fibers,biology,solid state physics,chemical kinematics,geochemistry,meteorology,electricity,and so forth.
Several methods were introduced for obtaining exact solutions of NLEEs.[33−54]Especially,the solutions of the electrical lattice equations is studied by several groups,where Eilbeck introduced some numerical solutions,[55]generalized discrete Lange-Newell criterion,[56]roguewave solutions,[57]Kudryashov method and the G′/G-expansion methods.[58]Moreover,some solutions of electrical lattice with nonlinear dispersion are presented as in Ref.[59],combination of rotating wave approximation and the Gardner-Morikawa transformation.[60]From the previous studies we can see that there small numbers of solutions were presented in the case of the electrical lattice with nonlinear dispersion,which motivated us to find efficient optical soliton solutions of this equation.
The remaining sections of this article are arranged as follows:Section 2 present the equation of the suggested model and it is mathematical analysis.The algorithms of the analytical methods,namley,Extended Auxiliary equation method and extended Kudryashov expansion method are used for solving the lower and upper forbidden and gab of the nonlinear Salerno equation,and we discuss the used method for obtaining the new optical solitons solutions in Sec.3.Finally,we conclude our findings in Sec.4.
2 Governing Model and Mathematical Analysis
This section introduces the model,which contains nonlinear logarithmic capacitance,as in the following equation,[12]
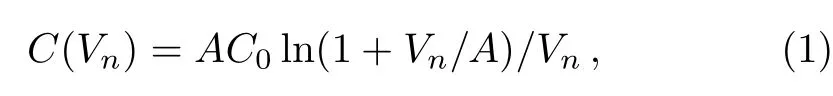
where A and C0are constants.By using the Kirchhoff law,we have
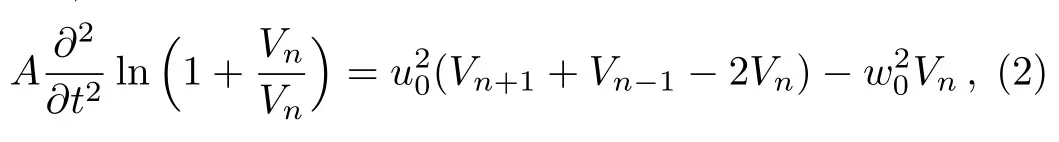
In order to solve Eq.(2),we assume
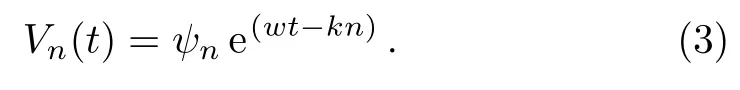
With the help of the previous equations,the Salerno equation in nonlinear case can be written as
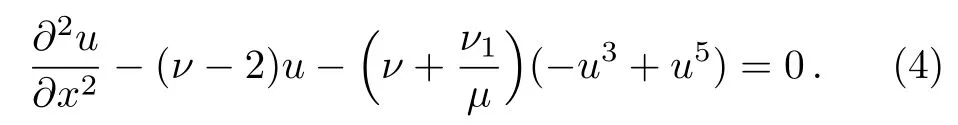
To obtain the optical solitons solutions of Eq.(4),the traveling wave solution is used as:
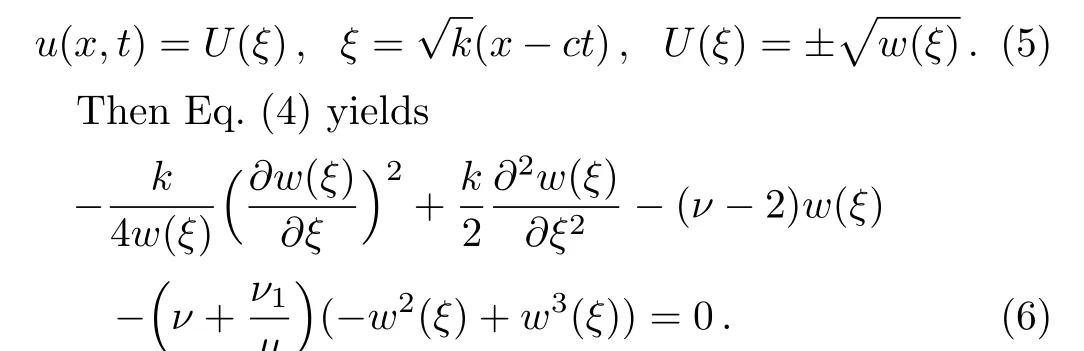
3 Solution Techniques of NLEE
For a given the general nonlinear PDE of the type
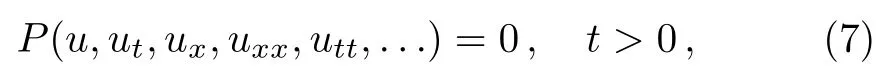
the function u(x,t)is an undefined function,P is a polynomial in u,t is the time variable,and x is the spatial variable.
Making use the traveling wave variable ξ=kx± ct,then Eq.(7)reads

the prime represents the differentiation with respect to ξ.In the next two subsections:
3.1 GKEM for Solving NLEE
The solution of Eq.(8)based on the above discussed method can be written as
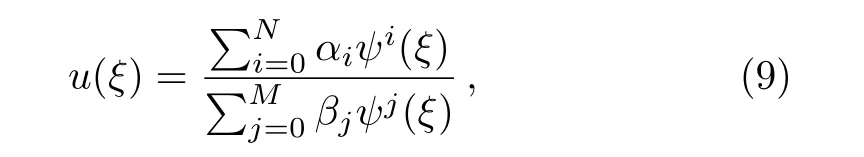
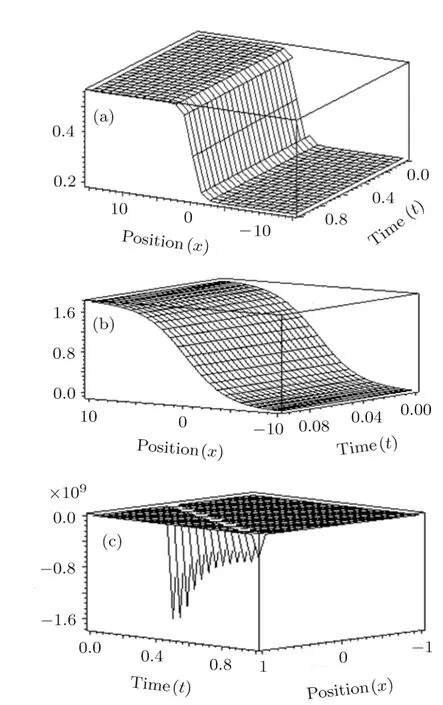
where αi, βj,(0 where A,α,β,and σ are constants.The integers N and M in Eq.(9)are obtained via the following relation where p,q,and s are integers. By substituting Eq.(9)and Eq.(10)into Eq.(8),then by equating all terms of same power to zero in ψi(ξ),(i=0,1,2,...).The next step is to find the solution of the group of algebraic equations for obtaining the values αi, βj,c,and δ.The obtained values are substituted in Eq.(9)considering the general solutions of Eq.(10)to find the exact solutions of Eq.(7),where the general solutions of Eq.(10)can be found in Ref.[34]. The exact solution of Eq.(6)can be found by generalized Kudryashov method as in the next steps.The highest order derivative w′′(ξ)and nonlinear term w3(ξ),are balancing,we obtain the equation N=M+1.By substitute M=1,resulting N=2,and Eq.(9)can be written as follows: Inserting Eq.(12)with the aid of Eq.(10)into Eq.(6)and collecting all power of ψi(ξ),resulting is a system of algebraic equations.The solution of the algebraic group of equations can be written as: In view of Eq.(13)with Eq.(12),we gain the bright,dark and sinulgar solitons,a combination of such solitons,and complexition solutions are revealed as follows: where ψi(ξ)is given as follows: Family 1In case of∆ = β2− 4ασ <0,σ≠0,ψi(ξ)reads Family 2In case of∆ = β2−4ασ >0,σ≠0,ψi(ξ)are Family 3In the limiting cas if ασ >0,β =0,then Family 4When β =0,σ = −α,then Family 5When β=k,σ=mk,β= α =0,β=k,α=mk,σ=0,then Once we obtained the solution of the differential equations,one we can plot the results as in Fig.1,where the solutions of Eqs.(18),(26),and(29)are present in Figs.1(a),1(b)and 1(c).respectively. Fig.1 The solitary wave solutions of Eq.(18)at Fig.1(a),Eq.(26)at Fig.1(b)and Eq.(29)at Fig.1(c)with a fixed values of k=1,c=0.1,a2=1;α=1,β=1,σ=1,A=0.1,and p=q=1. According to this method,the solution of Eq.(6)is expressed as where ψ(ξ)satisfies the Auxiliary equation below. where Ci(i=1,2,3,4)are determined later.To solve Eq.(6)via the used method.By balancing the highest order derivative w′′(ξ)and nonlinear term w3(ξ),we get N=1.Then Eq.(32)reads The same as in the previous section,making use of Eq.(34)with Eq.(33)into Eq.(6),collecting the same power of ψ(ξ)i,equating to zero,we have a set of algebraic equations.By solving it,it leads to Using Eq.(37)into Eq.(34),we gain the bright and dark solitons solutions and other solutions to Eq.(6)as follows Case1For C2> 0 and C4< 0, ψ(ξ)= Case 2For C2<0 and C4>0,ψ(ξ)= Case 3For Case 4For Figure 2 is the same as in Fig.1,where the solutions of Eqs.(36),(37),(38),and(39)are presented in Figs.2(a),2(b),2(c),and 2(d)respectively. Fig.2 The solitary wave solutions of Eq.(36)at Fig.2(a),Eq.(37)at Fig.2(b),Eq.(38)at Fig.2(c),and Eq.(39)at Fig.2(d)with a fixed values of parameters such as k=5,c=1,C2=1;C3=C4=0.5,α0= α1= α−1=1. We can see from the obtained results that are in good agreement with the existing ones in previous work,and in some cases go back to the obtained solutions and it is shown that the techniques used here are robust,accurate and easy to apply. In this article,two novel methods for constructing the optical solitons solutions for the nonlinear evolution equation have been considered.The GKEM and EAEM have been successfully implemented to devise new types of closed form traveling wave solutions in terms of hyperbolic function,rational function and trigonometric function.These obtaining solutions give a full description of the nonlinear dispersion information transfer through the electrical transmission lattice.The proposed methods establish that they are effective and powerful methods in obtaining the exact solutions of nonlinear evolution equations(NLEEs).This work can be extended using other interesting method as in Refs.[22–32],which can give more and new solutions in case of space-time fractional order,leading to our new task in future.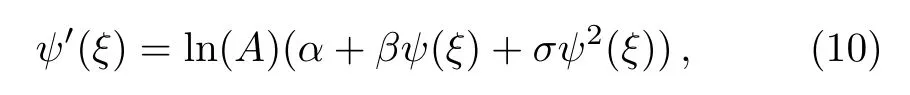
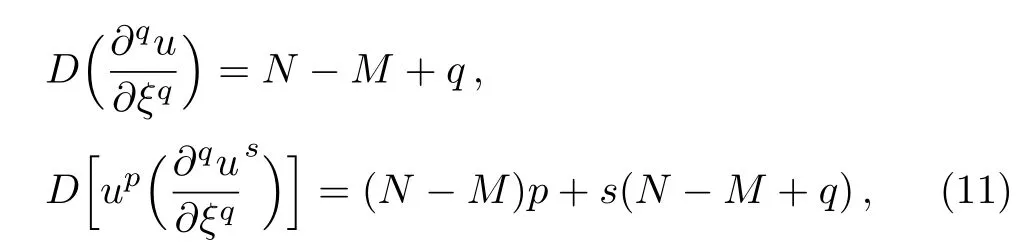
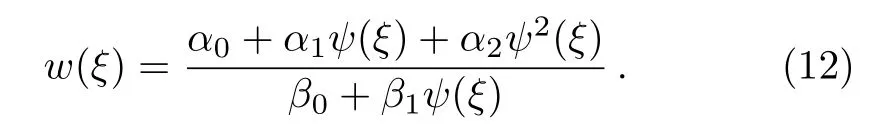
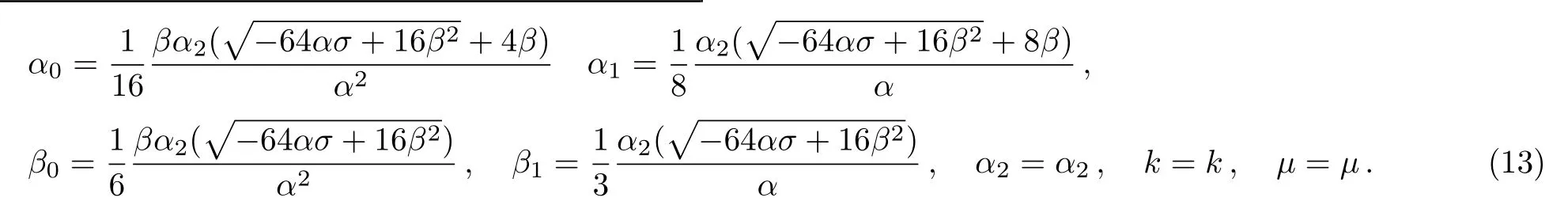



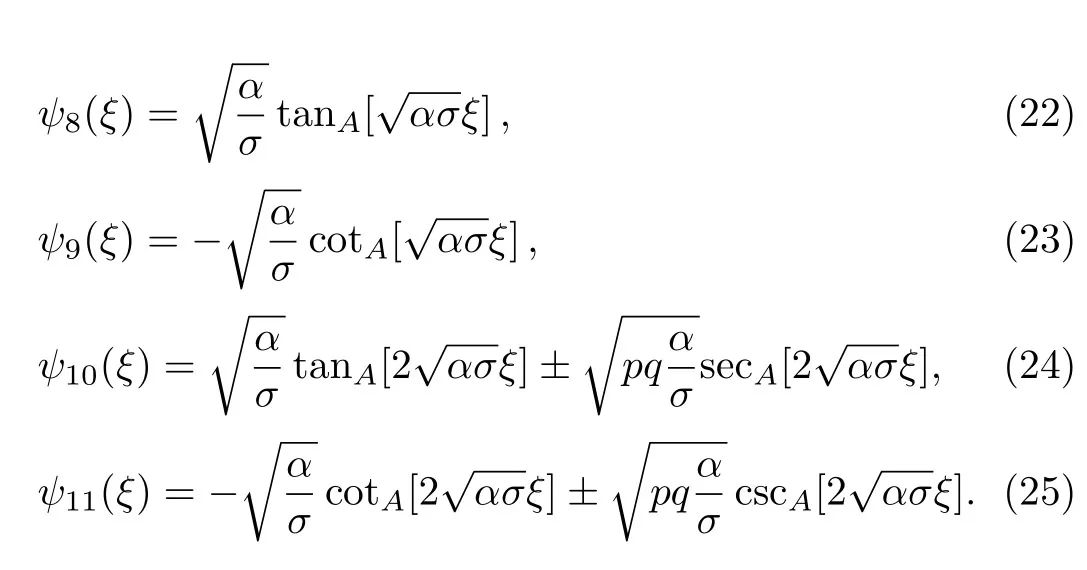
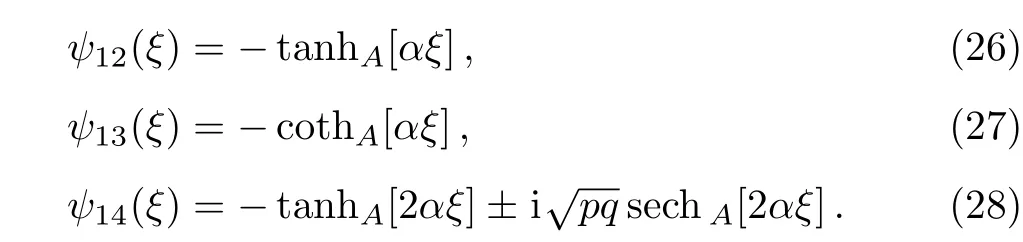

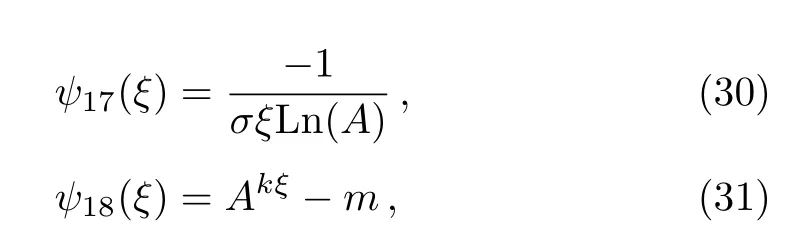
3.2 EAEM for Solving NLEE
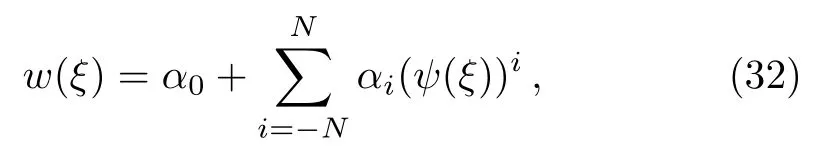
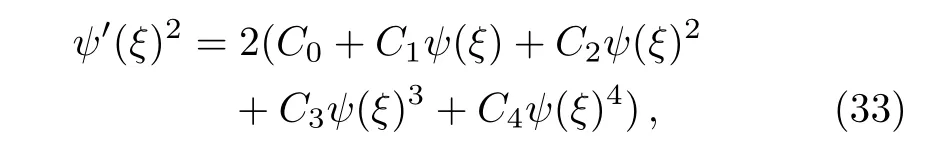
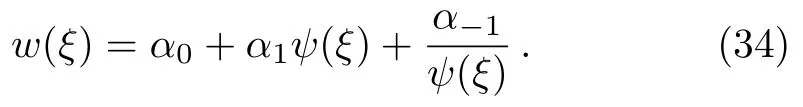
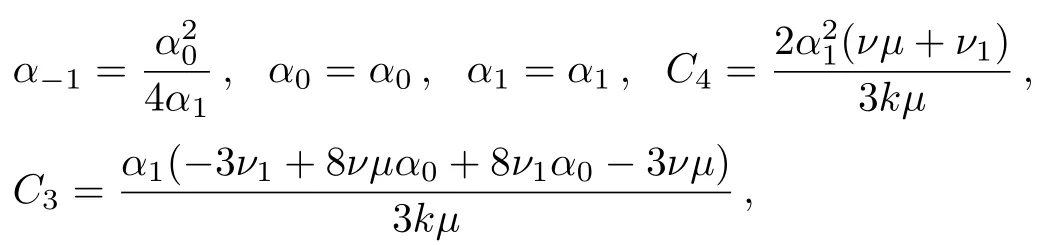
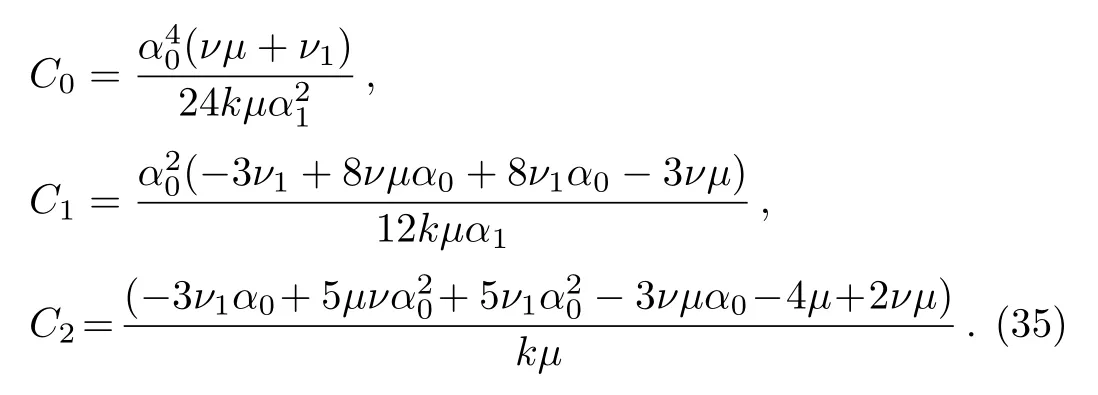
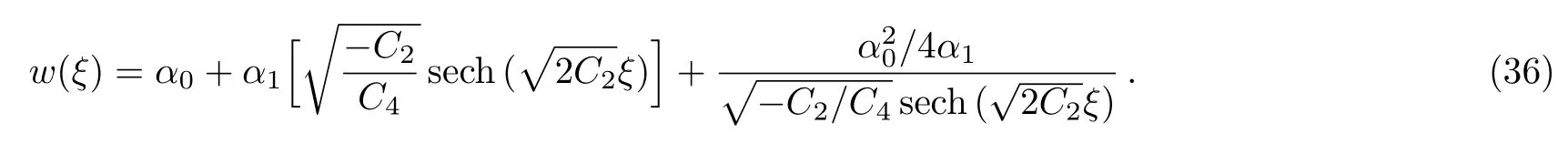
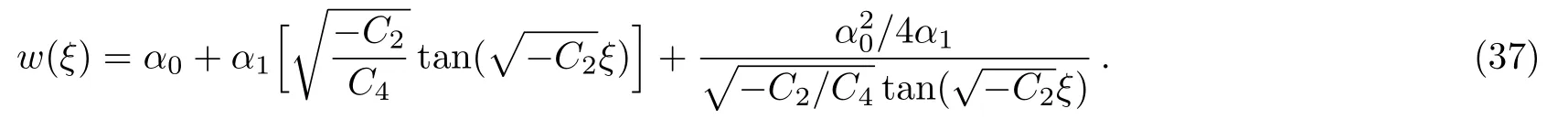

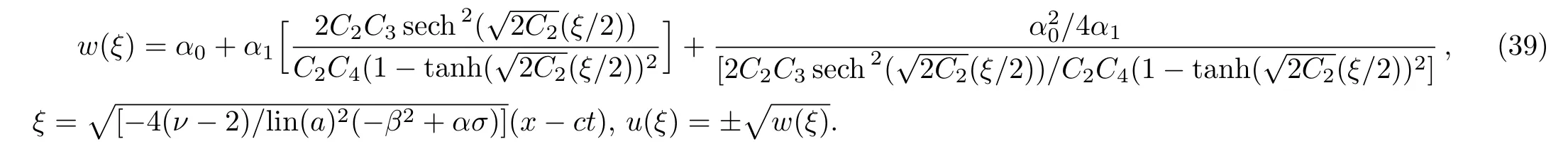
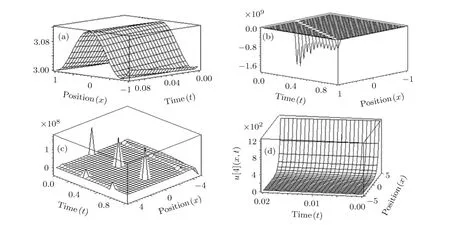
4 Conclusion
杂志排行
Communications in Theoretical Physics的其它文章
- Thermodynamics Properties of Confined Particles on Noncommutative Plane
- Numerical Analysis of Magnetohydrodynamic Navier’s Slip Visco Nano fl uid Flow Induced by Rotating Disk with Heat Source/Sink
- Coherence of Superposition States∗
- Exact Solution for Non-Markovian Master Equation Using Hyper-operator Approach
- Study of the FCNH Coupling with Boosted Higgs at LHC∗
- Comparison Between χ2and Bayesian Statistics with Considering the Redshift Dependence of Stretch and Color from JLA Data
