微生物动力学优化算法*
2019-09-14陆秋琴黄光球
陆秋琴,黄光球
西安建筑科技大学 管理学院,西安 710055
1 引言
在工程中存在很多具有大量局部最优解的优化问题,而且在很多情况下这些优化问题的目标函数和约束条件的数学表达式没有限制条件,传统的优化算法无法求解此类优化问题。目前,求解此类优化问题的方法是群智能优化算法[1]。与传统优化算法不同,群智能优化算法求解一个优化问题时,采用若干试探解同时进行演化计算,这种“群起而攻之”的方法可求解一些非常困难的优化问题[2]。然而,不存在一种群智能优化算法可求解所有类型的优化问题[3]。在群智能优化算法中,每个试探解被比喻成具有生物特征的个体,一些特殊生物进化场景被转换成群智能算法的逻辑结构,活跃在该场景中的生物个体之间的相互作用关系被用来构造生物个体的演化算子[4]。
种群动力学[5]是一门反映生物种群相互作用关系的数学理论,种群动力学包含有很多分支,每个分支均有改造成一种群智能算法的潜能。文献[6]基于Lotka-Volterra 模型构造出了一种特殊种群动力学优化算法,该算法利用3个种群间的相互作用关系即互惠共存关系、竞争关系、捕食-被食关系构建出进化算子,所有算子的演化特性可以确保算法具有全局收敛性。文献[7]采用种群动力学理论构造出了种群动力学优化(population dynamics-based optimization,PDO)算法。该算法将任意两种群间的捕食-被食、互利、融合、竞争、突变和选择等行为用于构造种群的进化策略。文献[8]基于种群动力学理论提出了一种改进的PDO算法。该算法被用来快速确定井下多点集中涌出矿尘就地消除最佳引导路径。文献[9]采用种群动力学中的捕食-被食理论提出了另一种改进的PDO算法,该算法可快速确定井下矿尘收集站、井下风机以及通风构筑物的最佳安装位置。
微生物培养是利用培养室培养一种或多种微生物种群,微生物培养动力学是研究培养室中在人类控制下微生物种群相互作用、不断演化的数学理论。微生物培养动力学是种群动力学分支之一[5]。为了利用微生物培养动力学的一些特殊性质来构造出高性能群智能优化算法,本文采用了一种带时滞影响的混杂食物链微生物脉冲培养动力学模型来构造微生物动力学优化算法(microbial dynamics optimization,MDO)。在该算法中,本文采用了与现有种群动力学优化算法不同的设计思路,提出了将微生物培养动力学模型转化为能求解某些优化问题的一般方法;构造出的算子可以充分反映培养系统中的有毒物质和培养液对微生物种群的影响以及微生物种群之间的相互作用关系,从而体现微生物培养动力学理论的基本思想。MDO 算法能够全局收敛,对求解维数较高的优化问题具有一定优势。
2 算法基本原理
2.1 MDO算法的场景设计
假设在微生物培养系统E中生活有N个微生物种群,即P1,P2,…,Pi,…,PN;每个种群不但以E中的培养液为食,而且还以E中的其他K个种群为食。在微生物培养过程中,周期性地向E中注入已调制好的新鲜培养液;与此同时,从E中不断移除无用的培养液;微生物种群吸收的培养液不会立即就转化成新的微生物种群,或者说,在从培养液向微生物种群转化这一过程存在一个时间段;随着培养液的注入,有害物质也随之注入。为了调控有害物质对种群的破坏性影响,必须不断评估种群受到有害物质的危害程度。培养系统的运行可通过对两个因素进行不同控制来实现:一是培养液中营养物质的浓度S;二是培养液的流量Q。浓度S的变化会引起微生物种群的生长产生变化。
微生物种群Pi的特征可用Pi={fi,1,fi,2,…,fi,n}表示,其中fi,j是Pi的特征j,n是每个种群的特征总数,i=1~N,j=1~n;E中培养液的营养物质浓度对种群Pi的影响体现在对种群Pi的特征的随机影响上。
假设所要求解的优化模型为:

式中,H为搜索空间;f(X)为目标函数;X为n维解向量,X=(x1,x2,…,xi,…,xn),xi为解分量。在H中任意选择N个初始解,即H={X1,X2,…,XN},其中Xi=(xi,1,xi,2,…,xi,n),i=1~N;培养系统E与搜索空间H相对应,优化模型的N个初始解与E中的N个微生物种群一一对应,即Xi与Pi一一对应;更精确地说,Xi的变量xi,j与Pi的特征fi,j一一对应。
综上,初始解与微生物种群是等价概念,以后不再区分。Pi摄入营养后,它的生长状态会产生变化,将该变化投射到H,等价于初始解Xi从空间位置a转移到b。一个空间位置称作一个状态,用它的下标描述。
假设Pi当前状态为c,此等价于在H中的位置为Xc。若Pi摄入营养后,从状态c演变到状态d,此等价于在H中从位置Xc跳转到位置Xd。按式(1)计算,若f(Xc)>f(Xd),表明位置Xc比位置Xd要优,则认为Pi强壮。反之,若f(Xc)≤f(Xd),表明位置Xd比位置Xc差,或没有区别(因f(Xc)=f(Xd)),则认为Pi虚弱。强壮的种群能以较高的几率不断生长,而虚弱的种群则有可能不再生长。
Pi的强弱可用微生物生长指数(microbial growth index,MGI)来表示。质量好的解对应具有较高MGI指数的种群,即强壮的种群,质量差的解对应具有较低MGI指数的种群,即虚弱的种群。对于式(1),Pi的MGI指数按下式计算:
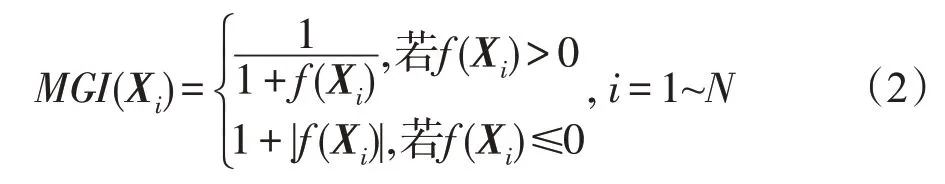
在E中,微生物培养的生物智能特征体现在如下几个方面:
(1)各种群因争夺培养液而存在相互影响,此类影响会在种群的某些特征间的随机相互作用上体现出来,此为“竞争的智能特征”。
(2)一个种群以另外一些种群为食,那些被食的种群的某些特征就会融入到该种群的某些特征中,此为“吃的智能特征”。
(3)任一种群的进化是通过不断向其他强势种群学习而取得的,此为“学习的智能特征”。
微生物培养的生物智能特征最终以生物演化算子的形式体现出来。所有微生物种群间的相互影响投射到式(1)的H中,就是解向量间存在相互作用。
MDO 算法就是采用此类策略来实现对式(1)全局最优解的求解。
2.2 微生物培养动力学模型
假设在培养系统E中共有N种微生物种群,每个种群既以培养液为食,又以E中L个其他种群为食。此外,有毒物质会毒害所有种群。时期t,种群Pi的浓度为yi(t),yi(t)≥0,i=1~N;培养液以流量Q流入到E中,其中营养物质的浓度为S0。该培养系统具有时滞影响的混杂食物链微生物脉冲培养动力学模型[5]如下:
式中,S(t)表示时期t培养液的营养物质浓度;μ0表示种群的相对增长系数;C0表示种群对培养液的消耗率;MS(t)表示时期t种群Pi捕获到的K个种群的编号的集合;K0、α0、γ0、W0表示与种群生长相关的常数;yi(t)表示时期t种群Pi的浓度;c(t)表示有害物质浓度,c(t)≥0;q0表示每个培养液投放时期输入的有害物质的数量;r表示种群因有害物质而毒害死亡的减少率,r>0;T表示培养液的投放周期;τ表示培养液向微生物种群转化的滞后时间;t+为培养液投放时间点;k表示正整数,k≥1。
在时期t,种群Pi的占比ri(t)按下式计算:

种群Pi的占比ri(t)越大,被其他种群捕食的几率也会越大。记时期t参数C0、Q、K0、S0、α0、μ0、r、γ0、W0、q0的取值分别为为方便计算,将式(3)改为离散递推形式,即:
若t≠kT,则:
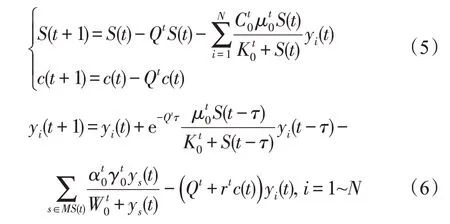
若t=kT,则:
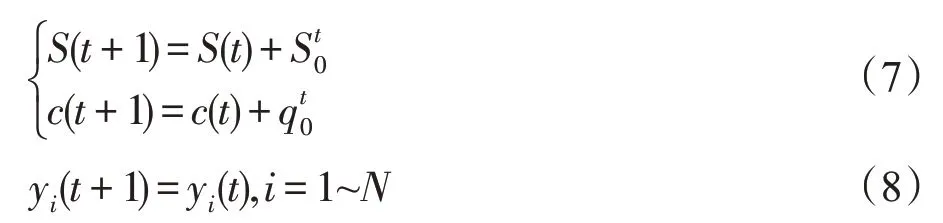
式(5)和式(6)中各参数的含义及其取值限制条件参见表1。
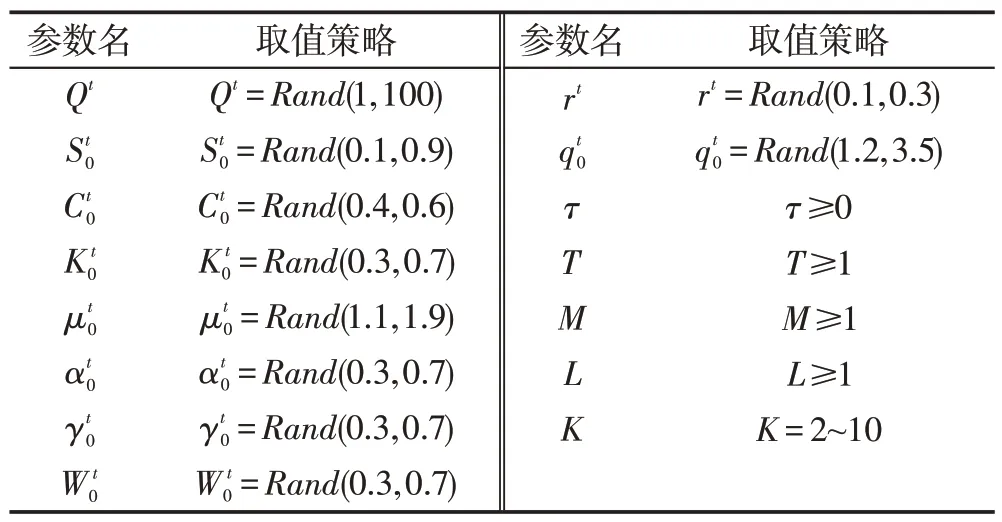
Table 1 Strategy of taking value for parameters of microbial dynamics model表1 具有微生物培养动力学模型参数的取值策略
表1中,Rand(A,B)表示在区间[A,B]生成一个服从均匀分布的随机数,A和B为常数,A≤B。
2.3 特征微生物种群集合的生成策略
时期t,设当前种群为Pi,特征微生物种群集合的生成策略如下:
(1)产生被食种群集合MS(t)。时期t,种群Pi以另外K个种群为食,即从N-1 个种群中分别以{r1(t),r2(t),…,rN(t)}为概率分布随机选择K个种群(但Pi不能被选中),这些种群形成集合MS(t),不妨设MS(t)={i1,i2,…,ik,…,iK},ik为种群的编号,k=1~K。
(2)分别产生30%、20%、10%强壮种群的集合FMt、GMt、HMt。时期t,先从N个种群中随机选出L个种群,这些种群的MGI指数要比当前种群Pi高30%,形成集合,其中s1,s2,…,sL是这些被选中种群的编号。然后从剩余的N-L个种群中随机选出L个种群,这些种群的MGI指数比当前种群Pi高20%,形成集合,其中g1,g2,…,gL是这些被选中种群的编号;最后从剩余的N-2L个种群中随机选出L个种群,这些种群的MGI指数比当前种群Pi高10%,形成集合,其中h1,h2,…,hL是这些被选中种群的编号。
(3)分别产生15%的强壮种群、虚弱种群、普通种群的集合ASt、BSt、CSt。时期t,从N个种群中随机选出L个强壮种群,其MGI指数要高于当前种群Pi的15%,形成强壮种群集合其中a1,a2,…,aL是这些被选中种群的编号;然后从N个种群中随机选出L个虚弱种群,其MGI指数要低于当前种群Pi的15%,形成虚弱种群集合,其中b1,b2,…,bL是这些被选中种群的编号;最后从剩余的N-2L个种群中随机选L个普通种群,其MGI指数与当前种群Pi的MGI指数没有关系,形成普通种群集合其中c1,c2,…,cL是这些被选中种群的编号。
2.4 微生物种群演化算子设计
MDO 算法利用微生物培养动力学模型式(3)来构造演化算子,从而实现培养系统与种群之间以及种群与种群之间的信息交换,进而实现对式(1)的搜索空间H的搜索。
(1)吸收算子。吸收算子描述的是种群Pi与另外K个种群之间的营养供给关系。将集合MS(t)中被食种群的一个随机选出的特征fs,j,s∈MS(t)传给当前种群Pi,使种群Pi获得生长:
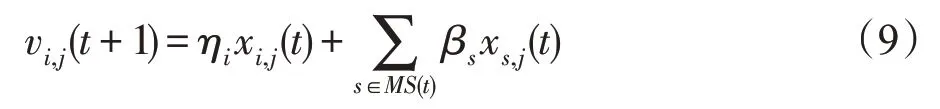
式中,xs,j(t)表示时期t种群Ps的特征j的状态值,即在时期t变量xs,j的取值;vi,j(t+1)表示时期t+1 种群Pi的特征j的状态值,即在时期t+1变量xi,j的取值;取βs=Rand(-0.95,0.95),ηi=Rand(0.45,0.65)。
(2)攫取算子。攫取算子描述的是一个种群攫取其他种群的优势特征,从而使其变得强壮。让FMt、GMt、HMt中的3L个强壮种群的特征fsl,j,sl∈{h1,h2,…,hL;g1,g2,…,gL;s1,s2,…,sL}所对应的优势状态值传给种群Pi的特征fi,j,使Pi变得强壮。假设当前种群为Pi进行优势攫取的特征为fi,j,则有:

式中,d1、d2、d3,e1、e2、e3,p1、p2、p3分别是从集合FMt、GMt、HMt中随机选出来的,且满足d1≠d2≠d3,e1≠e2≠e3,p1≠p2≠p3。
(3)混杂算子。混杂算子描述的是种群与种群之间的相互影响关系。对于当前种群为Pi,让ASt、BSt、CSt中的3L个种群的特征b1,b2,…,bL;c1,c2,…,cL}所对应的状态值经混杂融合后传给种群Pi的特征fi,j,则有:

式中,ρs=Rand(0.75,0.85),λi=Rand(0.65,0.85)。
(4)毒素算子。毒素算子描述的是外部系统中的有毒物质对微生物的毒害作用,该毒害作用能够在微生物种群之间传递。对于当前种群Pi来说,有:
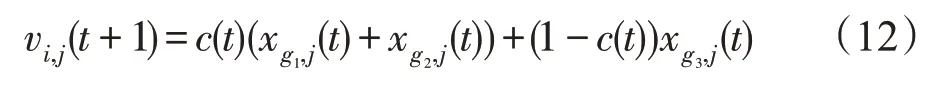
式中,g1、g2、g3是从{1,2,…,N}中随机选出来的,且满足g1≠g2≠g3。
(5)生长算子。生长算子的定义如下:
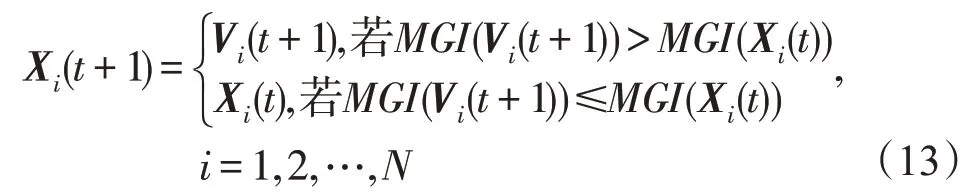
式中,Xi(t)=(xi,1(t),xi,2(t),…,xi,n(t));Vi(t+1)=(vi,1(t+1),vi,2(t+1),…,vi,n(t+1));利用式(2)计算MGI(Vi(t+1))和MGI(Xi(t))。
2.5 MDO算法
(S1)初始化:①令t=0,演化时期数G=8 000~60 000,误差要求ε=10-5~10-10,N=50~500,微生物种群被捕食的最高概率E0=1/1 000~1/100,K=2~10,T=1~10,τ=1~10,L=2~10。②随机确定{X1(0),X2(0),…,XN(0)},{y1(0),y2(0),…,yN(0)},S(0)。
(S2)执行下列操作:
Fort=0 toG
按式(4)计算r1(t),r2(t),…,rN(t)。
若T不能整除t,则按式(5)计算c(t+1)、S(t+1);若T能整除t,则按式(7)计算c(t+1)、S(t+1)。


2.6 算法特征分析
2.6.1 时间复杂度分析
MDO算法的时间复杂度计算过程如表2所示。

Table 2 Computation table of time complexity in MDO表2 MDO算法的时间复杂度计算表
2.6.2 MDO算法的收敛性分析
(1)Markov特性。从MDO算法的各算子的定义式(9)~式(12)知,时期t+1 任一新解的计算仅涉及该解在时期t时的状态,而与该解在时期t以前是如何演变到时期t时的状态的历程无关,表明MDO 算法的演变过程具有Markov特性。
(2)“步步不差”特性。从生长算子的定义式(13)知,时期t+1 任一种群的MGI指数永远不会低于其在时期t时的MGI指数,即MDO 算法的演变过程具有“步步不差”特性。
依据文献[10]可知,满足上述两个特性的MDO算法具有全局收敛性,其相关证明可参见文献[10],本文不再赘述。
3 MDO算法与其他算法比较
CEC2013[11]是国际上通用智能优化算法测试包,其中包括有28 个经过精心设计的基准函数优化问题。本文选用其中的15个基准函数优化问题来测试MDO算法的性能,如表3所示。
表3 中,O是n维向量,其值可随机产生。本文用MDO算法去求解表3中的15个函数优化问题,其参数是N=200,n=50,G=107,ε=10-7,E0=1/200,K=3,T=4,τ=3,L=3。与MDO算法进行比较的7种智能优化算法均选自国际著名期刊近期刊登的知名算法,这些算法如表4 所示,即RCGA(real-coded genetic algorithm)[12]、DASA(differential ant-stigmergy algorithm)[13]、NP-PSO(non-parametric particle swarm optimization)[14]、MpBBO(metropolis biogeographybased optimization)[15]、Copt-aiNet(artificial immune networks for combination optimization)[16]、SLADE(symmetric Latin-based adaptive differential evolution)[16]和GRABC(grab artificial bee colony algorithm)[17]。这7种算法的终止运行条件为:进化代数G=107或者最优解误差ε=10-7。
针对每个基准函数优化问题,上述8种算法分别独立运行51 次,以寻找全局最优目标函数。表5~表7 给出了每种算法所求得的最优目标函数值的平均值偏差、中值偏差、标准差、适应度评价次数。8种算法求解每个基准函数的性能排名是这些算法基于最优目标函数值的平均值偏差和适应度评价次数进行的排名;最终排名是基于8 种算法求解15 个基准函数所得的排名总积分而进行的排名。
非参数弗里德曼检验[19-20]是基于MDO算法所得的最佳结果与7 种被比较算法所获得的最佳结果之间进行的非参数检验,以确定MDO 算法产生的结果是否与7 种被比较算法所获得的结果有统计上的不同。弗里德曼检验的结果显示在表8 中,其中Significance=1 表示MDO 算法的性能与被比较算法具有99%的统计学差异,Significance=0 表示MDO算法的性能与被比较算法的性能没有显著差异。在表8中,Significance=1的案例数和Significance=0 的案例数分别表示MDO算法与7种被比较算法显著不同和几乎相同的求解基准函数优化问题的数目。
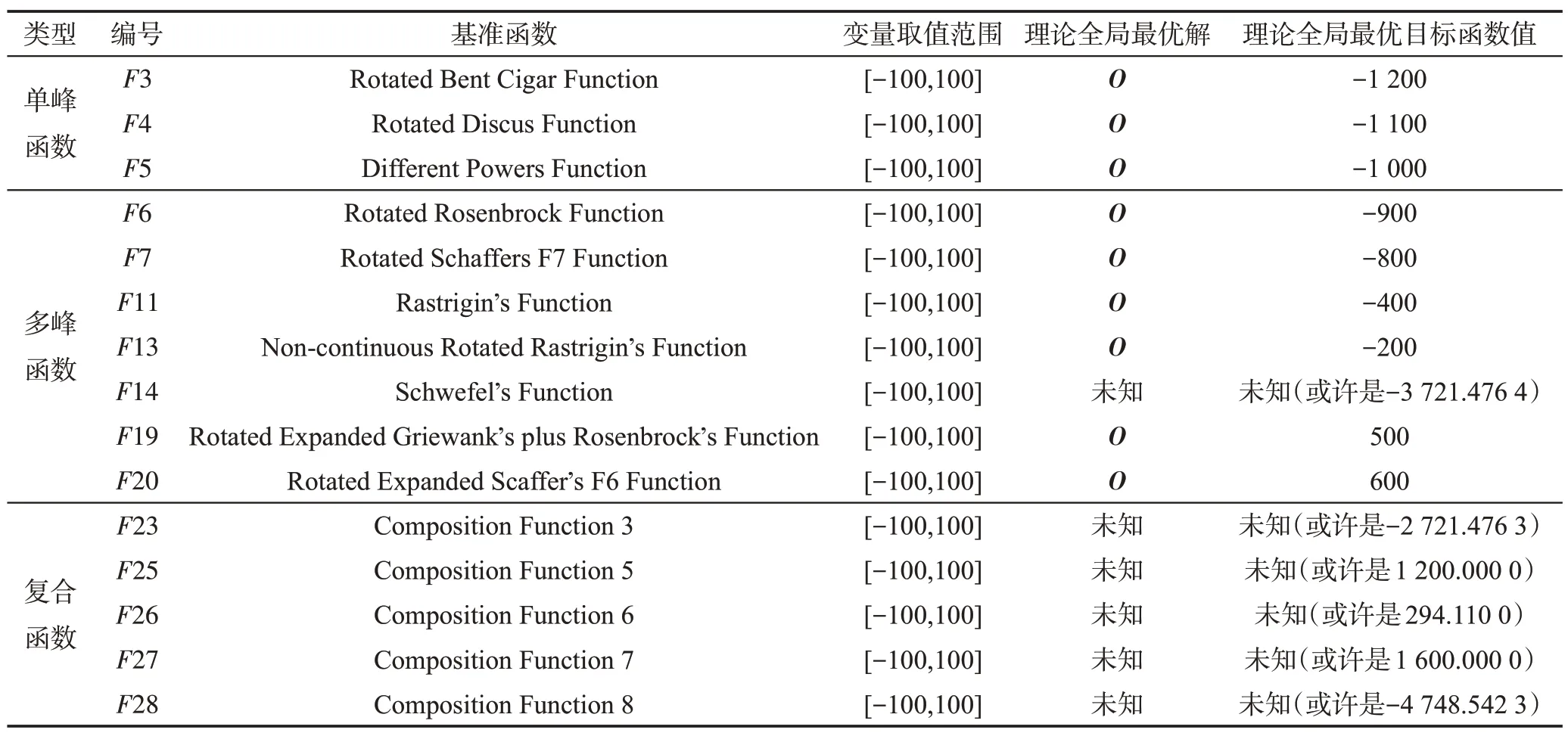
Table 3 15 benchmark function optimization problems表3 15个基准函数优化问题

Table 4 Parameters setting of compared intelligent optimization algorithms表4 参与比较的智能优化算法的参数设置
从表5~表7 可以看出MDO、RCGA、DASA、NPPSO、MpBBO、Copt-aiNet、SLADE和GRABC按平均最优目标函数值精度的排序如下:
MDO>SLADE>Copt-aiNet>NP-PSO>
DASA>RCGA=GRABC>MpBBO
从表8 可以知道,MDO 算法求解15 个基准函数优化问题的显著性案例总数为88,明显大于不显著性案例总数17,表明MDO 算法的性能明显优于7 种被比较的算法。
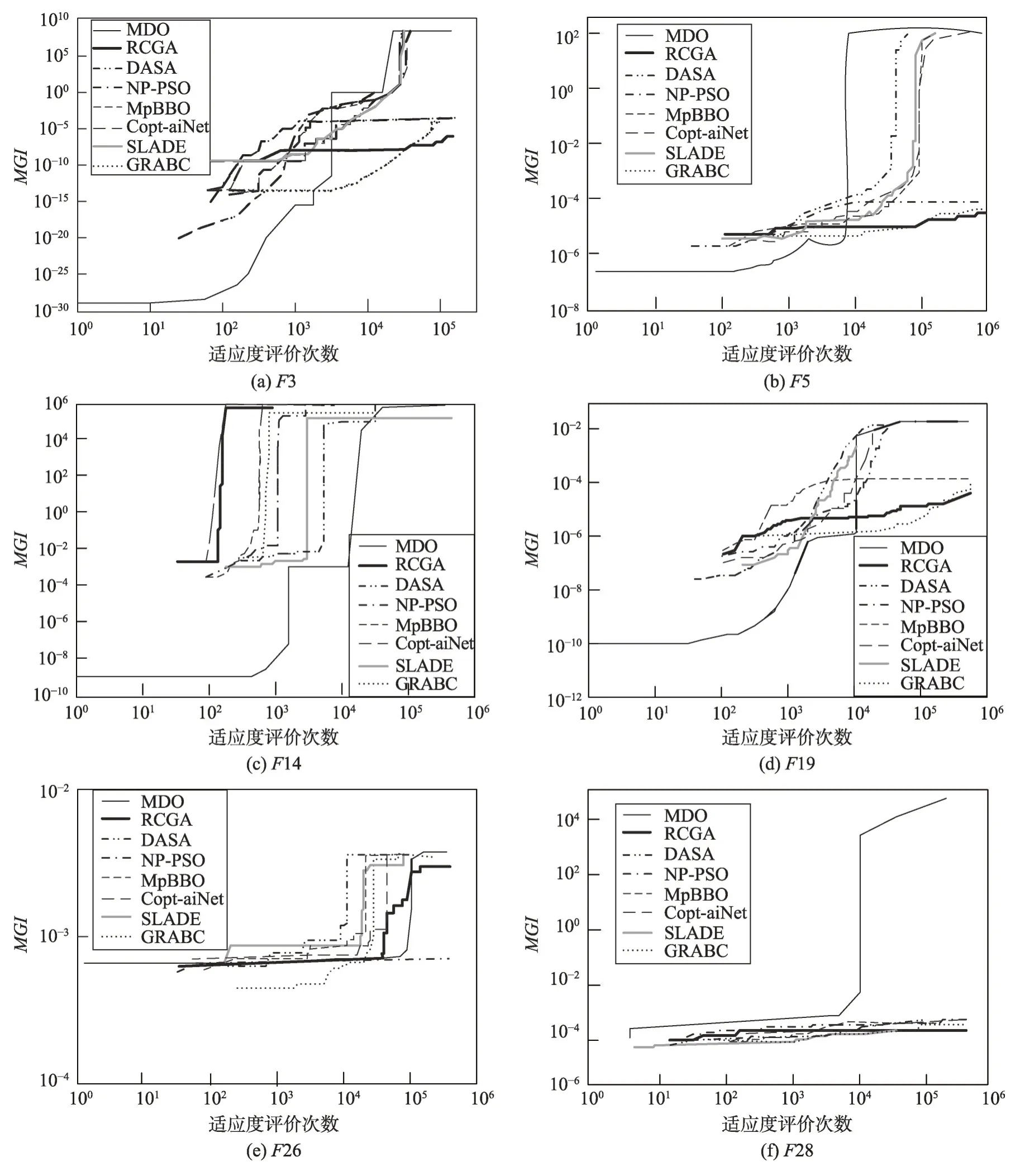
图1(a)~(f)说明MDO、RCGA、DASA、NP-PSO、MpBBO、Copt-aiNet、SLADE、GRABC 算法求解表3所示的6 个典型基准函数优化问题F3、F5、F14、F19、F26、F28 时的样本收敛曲线,图中水平和垂直轴采用对数刻度。从表5~表7可以看出,当MDO算法求解这6个优化问题时,均能以很高的精度发现全局最优解。综合看来,MDO 算法的综合性能要优于7种被比较算法,表明其求解精度高且计算速度快。
4 MDO 算法的局部寻优能力和全局寻优能力分析
4.1 穿透能力和扩展能力的测量方法
穿透能力和扩展能力用于描述MDO 算法在求解过程中陷入局部最优解陷阱后从陷阱逃逸并以一定精度收敛到全局最优解的能力。穿透能力用于描述MDO 算法在求解优化问题时或者快速从陷阱逃逸,或者快速收敛到全局最优解的能力;而扩展能力用于描述MDO 算法在求解优化问题时或者试探性跳出局部最优解陷阱,或者试探性提升最优解精度的能力。MDO算法的穿透和扩展能力可以通过微生物种群的行为来描述。当一个种群进行搜索时,其状态可以分为穿透状态和扩展状态。一个种群每次只能停留在一个状态:要么停留在穿透状态,要么停留在扩展状态。为了强调种群进入局部最优解陷阱的行为,将扩展状态再分为两个状态,一个称为膨胀状态,另一个称为粘滞状态。
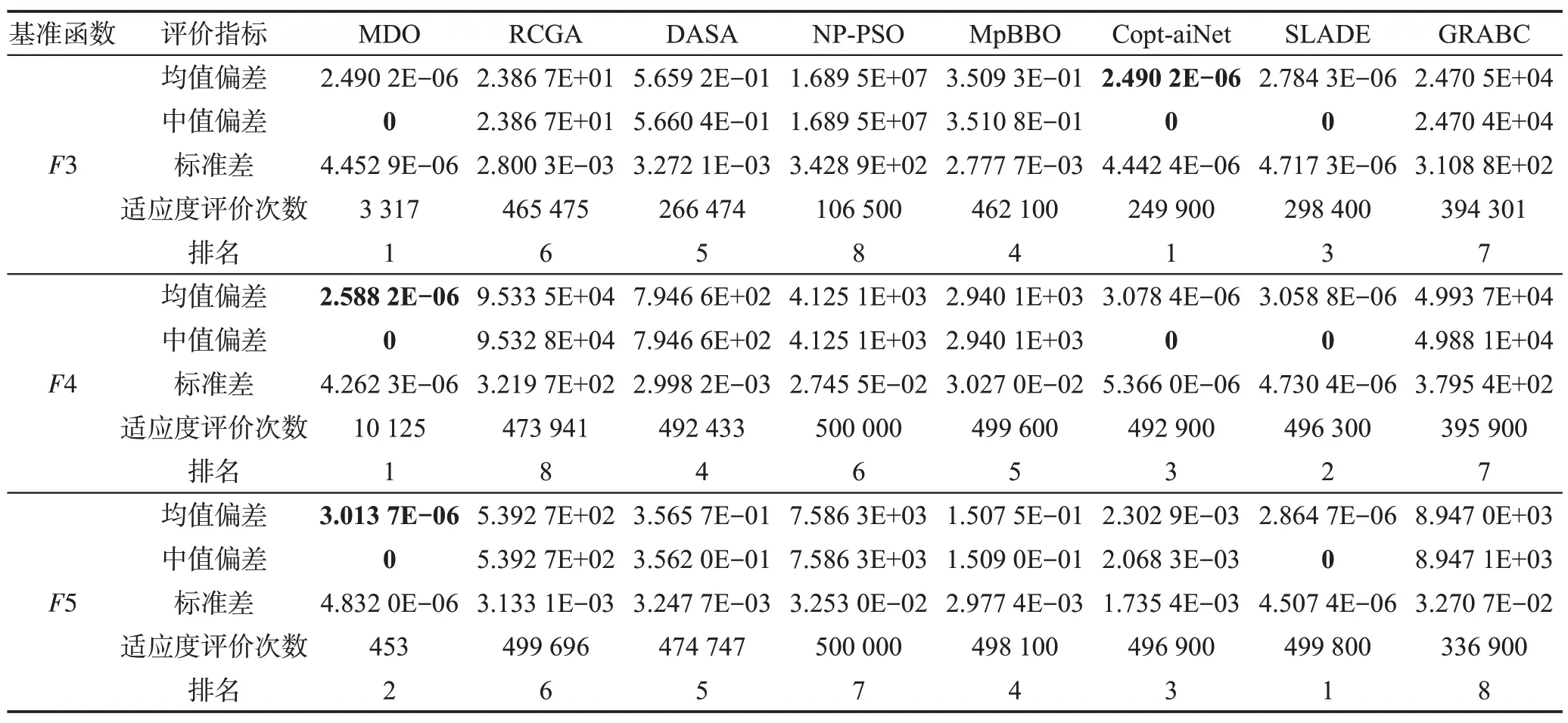
Table 5 Optimal solutions of all algorithms when solving unimodal benchmark functions表5 所有算法求解单峰基准函数时所得的最优解
当种群进行搜索时,如果种群的当前位置长期保持不变,认为种群已经陷入粘滞状态。两种情况可能会导致粘滞状态:一种是种群陷入局部最优解陷阱;另一种情况是种群的当前位置不能被其他种群抛出的信息更新。
当所有种群陷入粘滞状态时,搜索将自动停止,全局最优解将永远保持不变。另一方面,如果一些优化问题具有很高的条件数,那么当种群容易陷入粘滞状态时,提高全局最优解的精度总是困难的。
当MDO算法求解优化问题时,若穿透状态总是占优,则意味着搜索或者快速从陷阱逃逸,或者快速接近全局最优解,因此更高的穿透能力对于MDO算法是一件好事;若膨胀状态总是占优,则意味着搜索或者正在试探性跳出局部最优解陷阱,或者正在试探性提升当前最优解的精度,但可能耗费巨大的计算时间,因此算法的膨胀能力应该受到一定程度的控制;若粘滞状态占优,则意味着搜索几乎停止,因此必须完全避免粘滞状态。
穿透和扩展能力的评估可以基于四种收敛曲线:(1)任意种群的收敛曲线,跟踪任意一个种群搜索最优解的行为;(2)最佳种群的收敛曲线,其跟踪最佳种群搜索最优解的行为;(3)所有种群的平均收敛曲线,其跟踪所有种群在搜索最优解时的平均行为;(4)最佳收敛曲线,其跟踪所有种群在搜索过程中发现当前最优解的行为。
任意种群的收敛曲线可能会造成巨大的计算负担和计算机内存,因为在生态系统中有许多种群;此外,种群的行为太随机以至于无法控制它们。最佳种群的收敛曲线难以掌握,因为最佳种群可能随时间而变化。所有种群的平均收敛曲线与任意种群的收敛曲线相似,不仅可能造成巨大的计算负担和计算机内存,而且可以提高不良种群的MGI值,并压缩优良种群的MGI值。最佳收敛曲线可以在四条收敛曲线之间产生最小的计算负担和计算机内存,而且曲线不是关注任何单个种群,而是关注由所有种群产生的最佳行为。
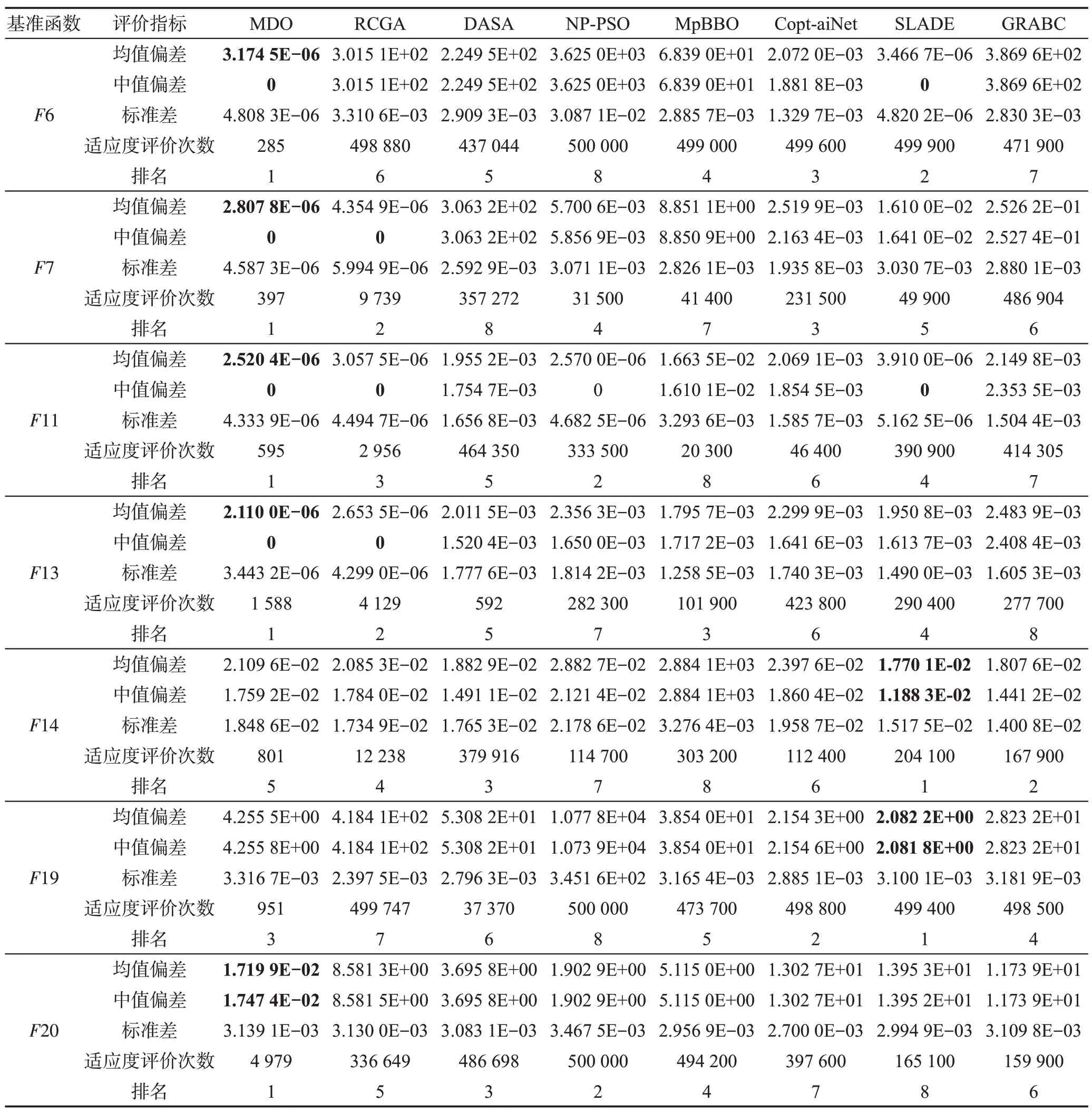
Table 6 Optimal solutions of all algorithms when solving multimodal benchmark functions表6 所有算法求解多峰基准函数时所得的最优解
MDO算法的穿透和扩展能力评价是基于最优收敛曲线的,是一种简单、直观的方法来判断MDO 算法的穿透和扩展能力。
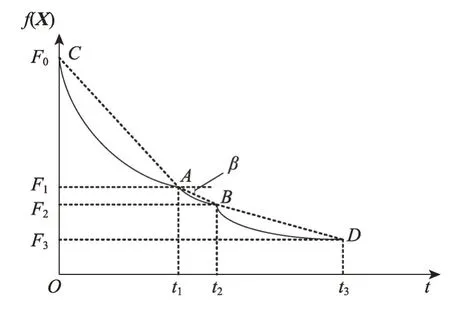
假设图2是MDO算法求解某个最优化问题时的最佳收敛曲线,C点是演化的起始位置,对应的最佳目标函数值为F0,CPU 时间t=0;当演化到达时间t=t1时,当前最佳位置处于A,对应于最佳目标函数值是F1;当进化到达时间t=t2时,当前最佳位置处于B,对应的最佳目标函数值是F2。种群的穿透和扩展能力可以通过直线AB的斜率来识别,因此有:
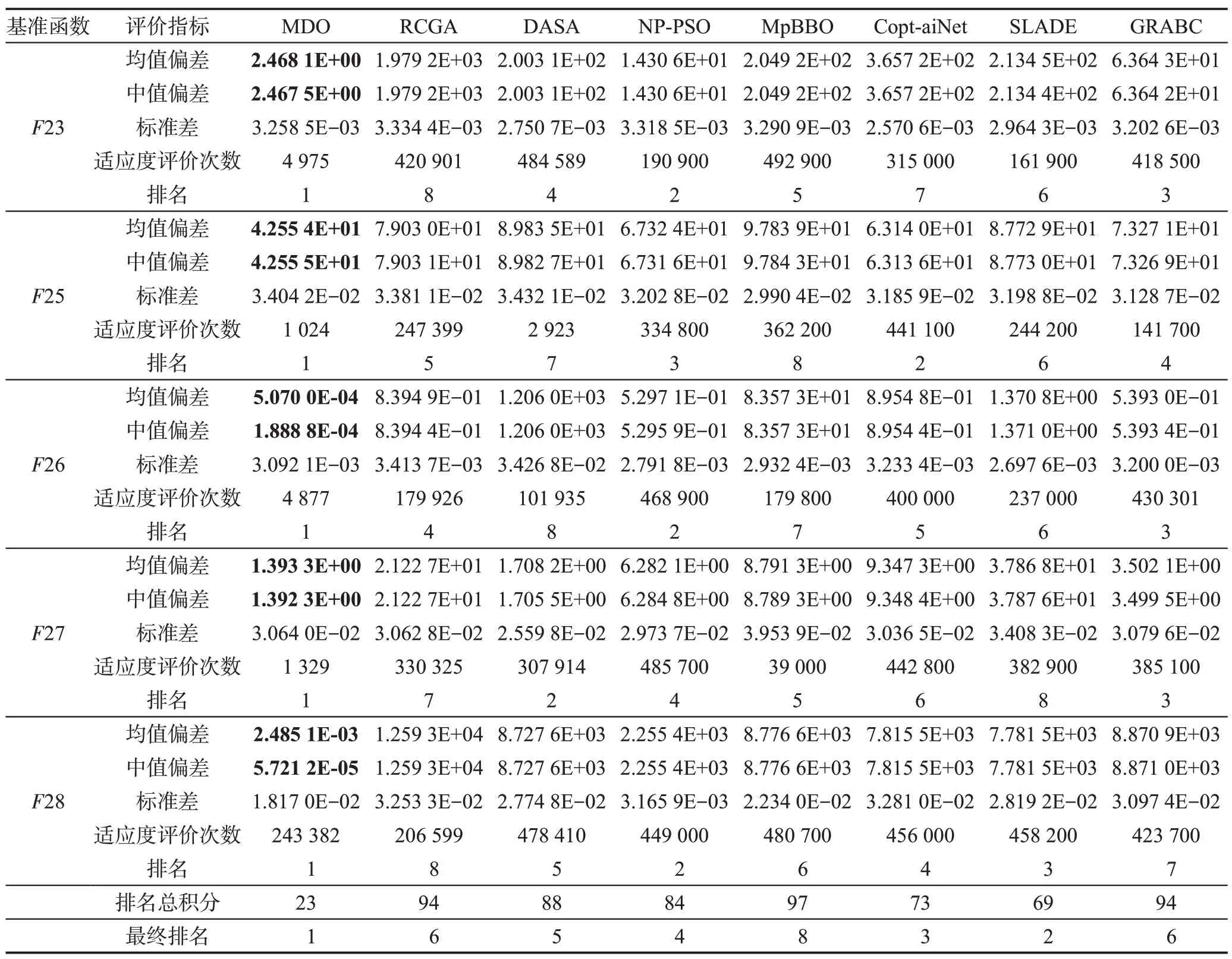
Table 7 Optimal solutions of all algorithms when solving composite benchmark functions表7 所有算法求解复合基准函数时所得的最优解
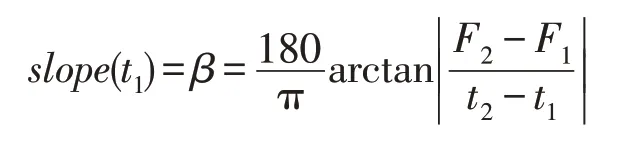
显然,若直线AB越陡,则穿透能力越高;若直线AB从陡峭向缓倾斜演变,则膨胀能力从好变坏,特别是当slope(t1)接近0时,膨胀能力变差,可能出现粘滞状态。因此,必须定义两个门限值λPs和λEs来说明这些情况:使用λPs来区分穿透状态(penetration state)和膨胀状态(expansion state),使用λEs来区分膨胀状态和粘滞状态(sticky state)。
(1)若slope(t1)>λPs,则意味着某些种群停留在穿透状态。
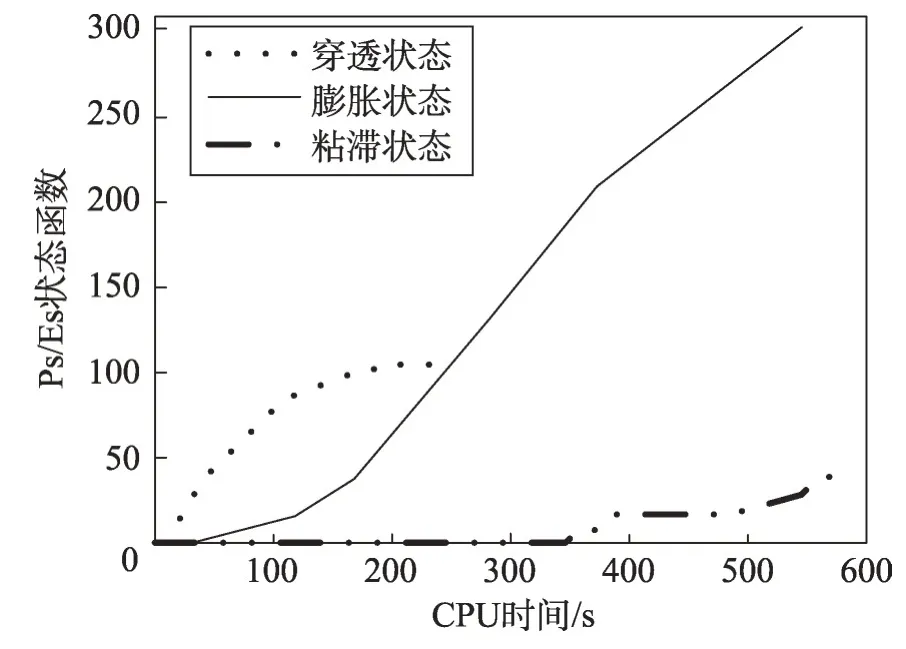
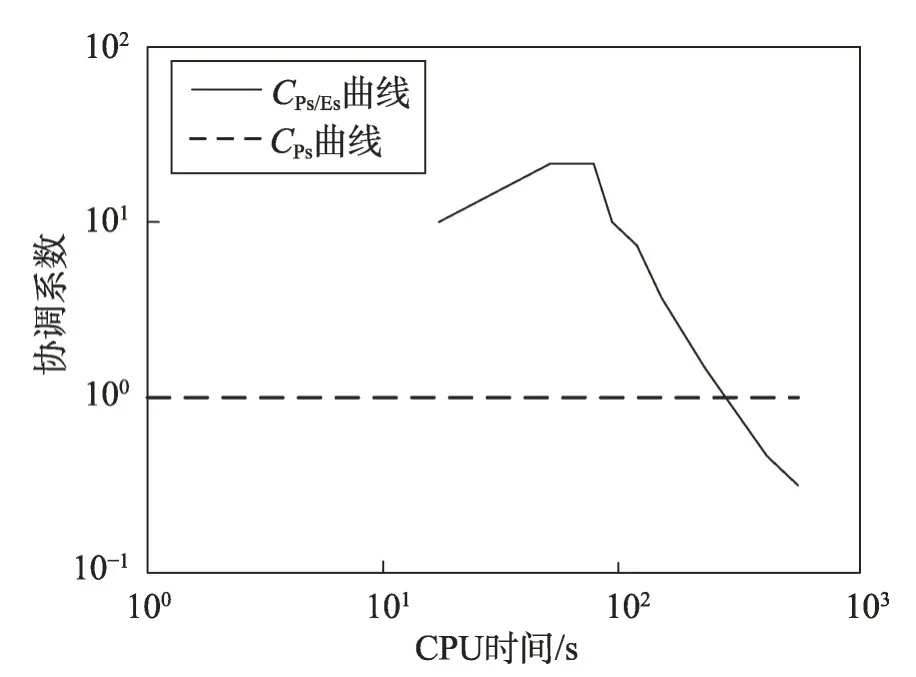
(2)若λEs (3)若slope(t1)≤λEs,则意味着大多数种群有进入粘滞状态的趋势,演化可能停止。 现在考虑种群在时间区间[tA,tB]中的穿透和扩展能力。让CountPs(tA,tB)表示在区间[tA,tB],tA≤t≤tB满足slope(t)>λPs的位置数;CountEs(tA,tB)表示在区间[tA,tB]满足λEs CountPs(tA,tB)=Count(i|slope(t)>λPs,tA≤t CountEs(tA,tB)=Count(i|λEs≤slope(t)≤λPs,tA≤t CountSs(tA,tB)=Count(i|slope(t)<λEs,tA≤t 其中,Count()是计算满足给定条件的位置的函数。 定义在时间间隔[tA,tB]内的穿透与膨胀协调度的测量方法如下: Table 8 Comparison of Friedman test results(α=0.01)表8 Friedman检验结果比较(α=0.01) 其中,CPs/Es(tA,tB)称为穿透-膨胀协调系数。 于是,有: (1)如CPs/Es(tA,tB)>CPs,则意味着搜索在时间间隔[tA,tB]内处于穿透占优状态。 (2)若CPs/Es(tA,tB)≤CPs,则意味着搜索在时间间隔[tA,tB]内处于膨胀占优状态。 类似地,可以定义在时间间隔[tA,tB]内的膨胀和粘滞之间的协调度的测量方法如下: 这里CEs/Ss(tA,tB)称为膨胀-粘滞协调系数。 于是,有: (1)如果CEs/Ss(tA,tB)>CEs,则意味着搜索在时间间隔[tA,tB]内处于膨胀占优状态。 (2)如果CEs/Ss(tA,tB)≤CEs,则意味着搜索在时间间隔[tA,tB]内处于粘滞占优状态。 选择Michalewicz 函数来说明MDO 算法的穿透能力和扩展能力。Michalewicz函数的形式为: 该函数具有如表9 所示的特性。Michalewicz 函数有n!个局部极值点,当n=80 时,其局部极值点有7.156 9×10118个,因此该函数极难求得最优解。 图3展示了MDO算法在时间间隔[0,694]中求解Michalewicz函数时的穿透、膨胀和粘滞状态的分布,计算参数为n=80,E0=0.005,K=3,T=4,τ=3,L=3,N=200,G=80 000。从图3可以看到,当MDO算法求 解Michalewicz 函数时,CountPs(0,694)=103,CountEs(0,694)=297,CountSS(0,694)=40,需要23.41%的时间来进行穿透,67.50%进行膨胀,只有9.09%的概率落入粘滞状态。 图4 展示了当MDO 算法求解Michalewicz 函数时,在时间间隔[0,694]中出现的穿透、膨胀和粘滞状态的数目。从图4 可以看出,当MDO 算法求解Michalewicz函数时,穿透和膨胀状态从0到250 s交替出现,但穿透状态从0到250 s总是占优;在250 s到350 s之间,只有膨胀状态发生;在350 s 之后,膨胀和粘滞状态交替出现,但出现粘滞状态的概率增加,膨胀状态总是在350 s之后占优。这意味着穿透和膨胀从0到250 s依次进行;在250 s到350 s之间,搜索接近全局最优,仅需要进行膨胀;当搜索进行了350 s 时,粘滞状态偶尔开始出现。 Fig.1 Convergence curves of all algorithms when solving 6 benchmark functions图1 所有算法求解6个基准函数时的收敛曲线 图5 展示了当MDO 算法求解Michalewicz 函数时,在时间间隔[0,694]中的穿透和膨胀之间的协调性。从图5可以看出,当MDO算法求解Michalewicz函数时,穿透状态从0到250 s占优;当t=250 s 时,穿透状态占优,达到最大值;250 s 后,穿透状态占优开始减少;相反,膨胀状态出现的概率开始增加。该结论与从图4所得到的结论一致。 图6 展示了当MDO 算法求解Michalewicz 函数时,时间间隔[0,694]中的膨胀和粘滞之间的协调性。从图6可以看出,当MDO算法求解Michalewicz函数时,当t=350 s 时,膨胀状态占优达到最大值,之后,占优状态出现次数开始减小。相反,粘滞状态出现的次数开始增加,但粘滞状态出现的次数总是不占优势。 Fig.2 Evaluation of penetration and expansion capacity of MDO algorithm图2 MDO算法的穿透和扩展能力评价 Table 9 Characteristics of benchmark function F3 and Michalewicz function表9 基准函数F3 和Michalewicz函数的特征 Fig.3 Distribution of penetration,expansion and viscosity(ε=1.0E-11,λPs=1.0,λEs=1.0E-10)图3 穿透、膨胀和粘滞状态分布(ε=1.0E-11,λPs=1.0,λEs=1.0E-10) Fig.4 Number of times of penetration,expansion and viscous state(λPs=1.0,λEs=10-10)图4 穿透、膨胀和粘滞状态出现次数(λPs=1.0,λEs=10-10) Fig.5 Variation of coordination coefficient of penetration and expansion with time(CPs=1.0)图5 穿透-膨胀协调系数随时间的变化规律(CPs=1.0) 从以上分析可知,当MDO算法求解带海量局部最优解优化问题和带高条件数优化问题时均表现出很好全局寻优能力,且其局部寻优能力和全局寻优能力的平衡性把控得较好。 本文基于带时滞影响的混杂食物链微生物培养动力学理论提出了一种具有全局收敛性的新型优化算法,与其他典型群智能算法相比,MDO算法具有如下特点: Fig.6 Variation of coordination coefficient of expansion and viscosity with time(CEs=1.0)图6 膨胀-粘滞协调系数随时间的变化规律(CEs=1.0) (1)吸收算子、攫取算子、混杂算子和毒素算子可增加其搜索能力。 (2)采用随机方法确定各算子中的相关参数,既大幅减少了参数输入个数,又使模型更能表达实际情况。 (3)算法所涉及的微生物培养过程充分体现了多种微生物种群的浓度、培养液投放量及其营养物质浓度、培养液定期投放量中含有的有毒物质浓度、培养液投放周期、培养液向微生物转化的滞后时间等参数的复杂变化情况。 (4)所有算子是通过利用具有时滞影响的混杂食物链微生物脉冲培养动力学理论以及微生物种群间的相互作用关系来进行构造的,不需要与求解的优化问题相关。因此,MDO算法具有很好的普适性。 (5)培养液及其所含有的有毒物质的浓度的脉冲增加会导致试探解从一个状态突然转移到另外一个状态,这种性质有利于使搜索跳出局部最优陷阱。 (6)算法考虑到了微生物种群培养过程中外界因素的不连续间断介入的现象。 (7)算法所涉及的微生物种群之间的相互作用丰富多彩,体现了培养系统中微生物种群间的复杂捕食-被食关系和竞争关系。 (8)算法体现了微生物培养动力学模型中各参数的复杂变化情况。 (9)在进行迭代计算时,算法每次只处理每个种群特征数的1/1 000~1/100,从而使时间复杂度大幅降低。因此,MDO算法适于求解高维优化问题。 MDO算法的下一步改进方向如下: (1)利用微生物培养动力学模型优化MDO算法的相关参数,使得这些参数设置更合理。 (2)深入研究吸收算子、攫取算子、混杂算子和毒素算子的动态特征。 (3)深入研究微生物种群的动态特征。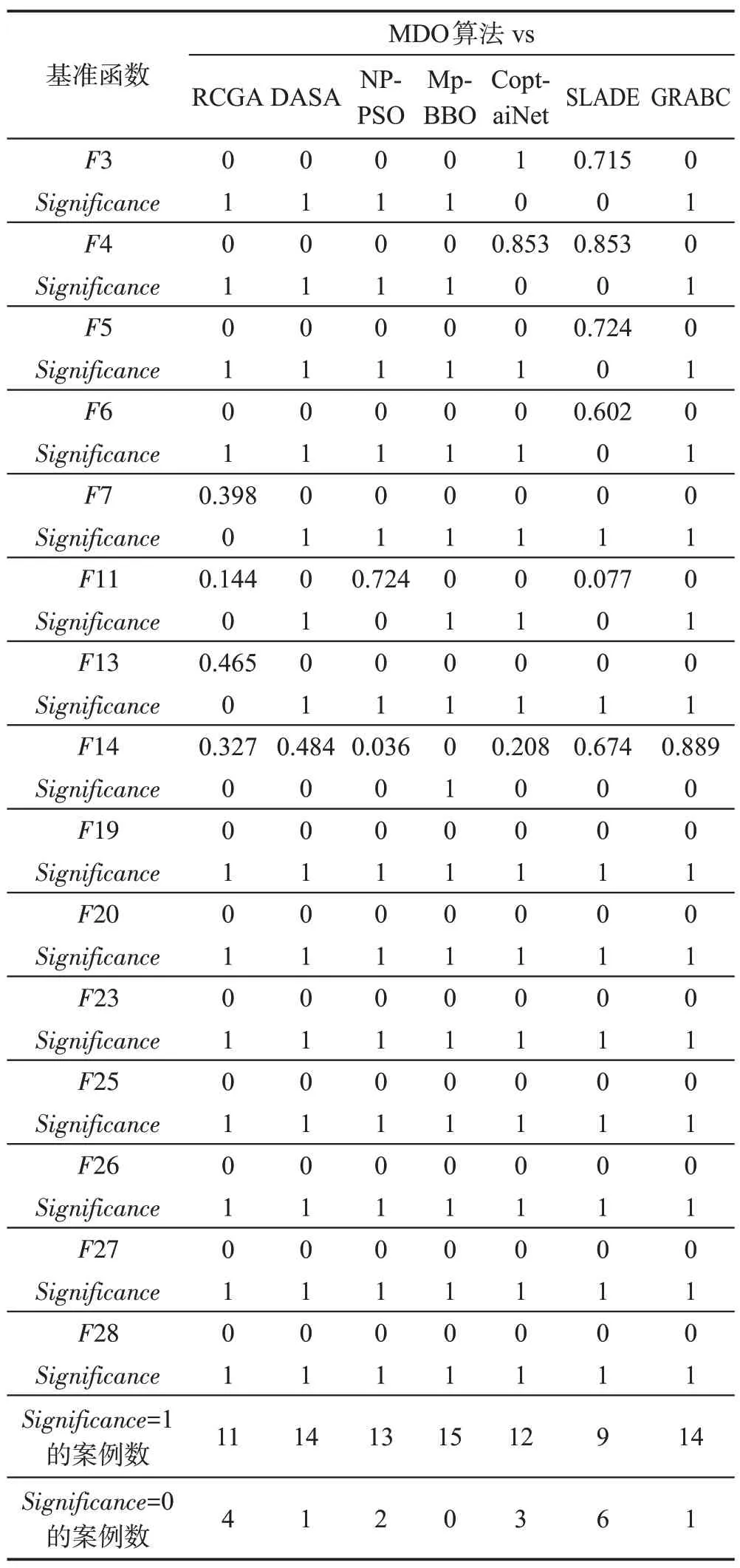

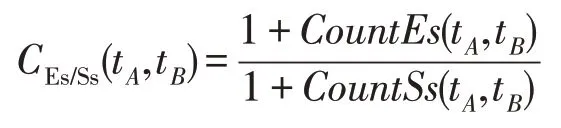
4.2 穿透与扩展能力分析
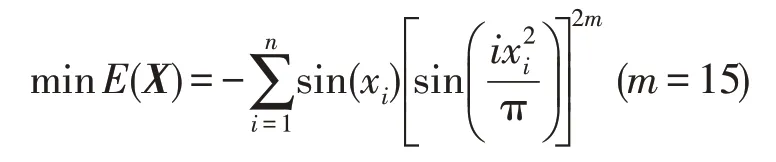
5 结束语