周 林，刘先省，方拥军，金 勇

(河南大学计算机与信息工程学院，河南 开封 475004)

0 引言

多传感器协同探测系统中，融合中心为了获得被跟踪目标的“统一”信息(包括时间和空间上的“统一”)，必须首先要在各分布平台上修正传感器量测，即消除不“统一”的多传感器量测误差。量测误差主要包含两类：随机误差和系统偏差。前者可以通过滤波等方法消除，而后者则需利用配准方法来改善[1]。系统偏差配准的目的是对传感器量测(诸如，雷达径向距和方位角测量、时钟误差、传感器位置等)偏差进行估计和补偿，以提高目标定位和跟踪精确性。

传统上，研究系统偏差配准问题时通常假设系统偏差先验信息已知，即系统偏差在整个探测周期是某一未知固定值或呈现缓慢动态演变，此时可利用最小二乘法、最大似然法、加权最小方差法、智能法、信息法、滤波等进行解决[2-7]。但由于探测区域气候、地形及照射光线各异、外来人为干扰增多、系统非线性和多模型等问题，导致系统机动以及系统偏差演化都难以建模，呈现随机性、突发性等特性。传统系统偏差估计方法不再适用解决随机性的系统偏差配准问题。因此，考虑充分利用序贯量测信息，进而准确、实时估计随机性系统偏差就尤为重要。

在利用多传感器序贯量测信息，通过构造目标函数，进而解决系统偏差估计的时候，无论目标函数中的参数有无约束条件，拟牛顿法、共轭梯度法、可行方向法等典型策略都取得了较好效果[8-10]。但上述方法通常找到的是平稳点或驻点(即局部最优点)，甚至找不到局部解，进而也较难找到所有极小点集合中的最好点(即全局最优点)。尽管全局最优算法的设计非必需，但它有助于解决优化问题，常见的优化算法包括遗传法、粒子群法、蚁群法、区间方法等[11-14]，它们具有全局最优性和良好的约束条件适应性，但实时性差、较难获得易验证的全局最优性条件。因此，考虑引入凸优化方法来求解全局最优解，该方法时间复杂度小，可用于可靠和迅速地优化模型求解。

研究发现Metropolis-Hastings(简称M-H)算法是一种近似贝叶斯方法[15-16]，属于有约束的后验概率最大问题，新样本的选择误差会不断增加，从而导致鲁棒性得不到保证。因此，本文以文献[16]中的系统偏差最大似然函数为基础，构造系统偏差估计的拉格朗日乘子二次函数并讨论构造函数的凸性，进而提出基于凸优化的系统偏差估计方法。

1 问题的描述

正如前面所述，当复杂环境或未知因素等出现时，导致系统以及系统偏差动态模型难以构建,传统方法不再适用。假设某一传感器探测系统中，考虑两个问题：1)机动目标的状态难以建模；2)考虑传感器量测受外界随机干扰。因此，可只对极坐标系下系统的非线性量测建模：

(1)

为讨论方便，将每个传感器极坐标系下量测模型转换为笛卡儿坐标系下，其模型如下：

(2)

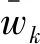
由于机动目标状态模型未知，若想获取估计系统偏差和目标状态信息，可利用zk={zk(i);i=1,…,n}及似然函数最大化方法估计传感器系统偏差bk和目标状态xk，即：

(3)

对n部传感器，假设量测具有白噪声，进而可得量测似然函数：

(4)

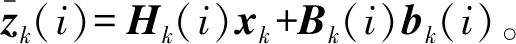
(5)

式(5)中,K2是常数K1的对数。忽略不相关常数项，通过优化得出目标最大似然估计：

清代乾隆年代[12]，江河商运发展，博罗老城、惠东梁化、惠阳的淡水、多祝又逐渐成为惠州区域主要的商业圩镇，陆续发展兴盛。宋、清惠州两次人口的暴增[13]，导致当地民间信仰祭祀场所对应惠州人口的聚居点而增加，罗浮山道教也两次借机复兴。同时，惠州地貌的特征使得台地、丘陵、平原阶地沿东江相间分布，造就治水民间信仰随人口聚居沿东江分布。

(6)

利用贝叶斯估计理论，得出多目标最大似然估计函数如下[16]：

(7)

2 基于凸优化的系统偏差估计方法

2.1 拉格朗日乘子二次函数

凸优化模型可对一般非线性优化模型进行局部逼近，是研究非线性规划问题的主要途径。本节将式(7)的系统偏差的最大似然估计函数转化为具有目标函数、约束函数的优化问题，其中目标函数核心是构造拉格朗日乘子二次函数形式，约束函数既包含求解参数空间边界不等式约束条件也包含量测差形式的等式约束条件。同时，对上述优化问题的凸性进行判断分析。

解优化问题用到的目标函数和约束函数即使是光滑的，有时候仍很难求解。为了更好描述后验概率函数并用优化函数条更精确估计参数，目标函数和约束函数之间的数学关系通过表达式描述，即用拉格朗日乘子二次函数表示，以第i个传感器为例，其拉格朗日乘子二次函数为：

(8)

式(8)中，L表示系统偏差拉格朗日二次函数；γ表示包含待估系统偏差的表达式；λ1、λ2、λ3分别表示约束条件系数，它们根据实际问题取值；f1、f2、f3分别表示约束条件。

传统求解拉格朗日乘子二次函数最优解的方法是用二次函数对待求参数求偏导并令偏导表达式等于零，进而得到解析解。尽管该方法易于数学描述，但弊端是当目标函数非凸(或非凹)时，函数局部极值的存在会导致函数全局最优解得不到确保。由于凸优化模型是研究非线性规划问题的主要途径，因此，可对上述拉格朗日乘子二次函数进行凸性判断。若函数呈现凸性，则其最优解可利用凸优化技术直接求解；若函数呈现非凸性，则可利用约束条件松弛、对偶等措施将非凸问题转换为凸问题之后再求解。

2.2 二次函数的凸性判断

判断函数凸性的充要条件是函数的Hessian矩阵为半正定阵。求拉格朗日乘子二次函数L(γ,λ1,λ2,λ3)对系统偏差bk的Hessian矩阵，并将前述的A、γ等代入，可得如下Hessian矩阵表达式：

(9)

上述已用凸优化方法证明拉格朗日乘子二次函数的凸性，结合拉格朗日乘子方法求解目标函数，可将拉格朗日乘子二次函数最优化问题等价为有约束的凸优化问题，具体表达式如下：

(10)

L(γ,λ1,λ2,λ3)=

(11)

因此，根据拉格朗日乘子二次函数表达式，本文通过Matlab软件附带的专业凸优化工具包来获得每一个采样时刻k使L最小的系统偏差bk。

2.3 算法描述

已有研究中，推导出的系统偏差最大似然估计函数，可利用M-H方法进行寻优求解，从而稳态模拟参数贝叶斯估计方法[16]，但该方法存在两个问题：1)本质上是一种迭代采样方法，马尔科夫链的链长影响算法的实时性。2)通常较易找到局部最优点而非全局最优解。因此，为了提高估计实时性和全局最优性，本文提出基于凸优化的系统偏差估计方法，其流程如下图1所示。

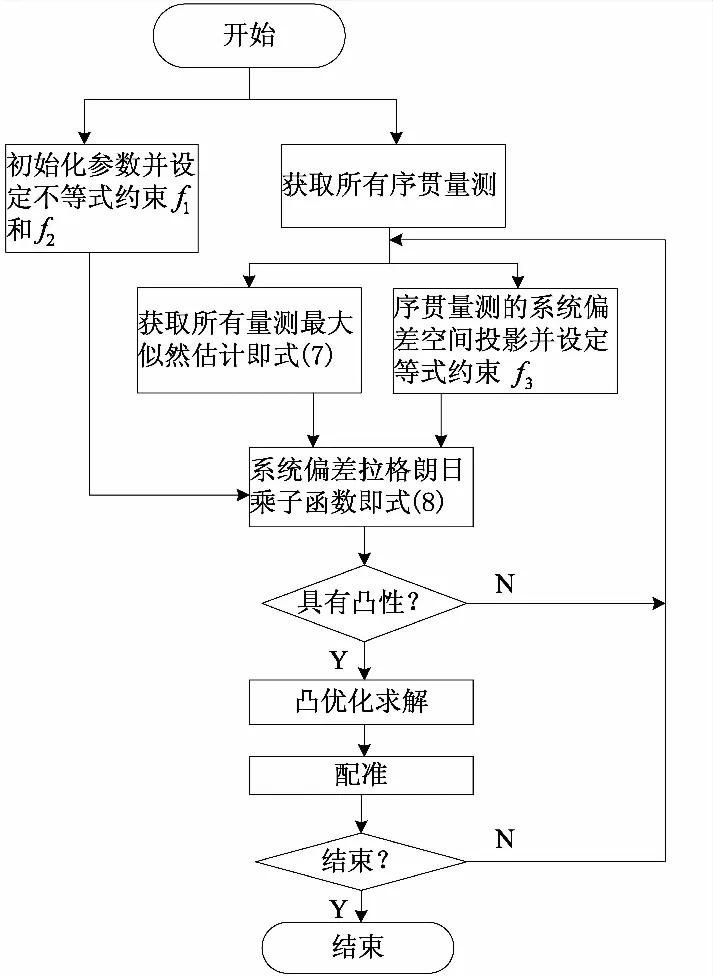
图1 算法流程图Fig.1 The flowchart of algorithm

3 仿真结果与分析

为了验证所提算法可行性和有效性，仿真假设用配置在异地的两部传感器探测和跟踪机动目标，且机动目标在2D坐标系统中的运动模型如下：

同时，两部传感器都设定为二维极坐标量测方式，即量测包含径向距和方位角，其量测模型如下：

zk(i)=hi(xk)+bk(i)+wk(i)i=1,2

(12)

式(12)中，传感器量测zk(i)=[ρk(i)θk(i)]T；量测噪声分别为σρ(1)=150 m，σθ(1)=0.5°；σρ(2)=80 m，σθ(2)=1°，非线性测量函数hi(·)如下：

(13)

式(13)中,i=1,2, 且(ζi,ηi)为笛卡儿坐标系下传感器位置， (ζ1,η1)=(300 km,-200 km)，(ζ2,η2)=(80 km,75 km)。

假设系统偏差bk具有随机性(即动态演化模型未知)，其估计初始b0=[0 0 0 0]T。为了验证所提算法的可行性和有效性，将本文算法与先前研究的M-H算法和ML算法进行比较。为了描述系统偏差的随机性，本文凸优化算法的待估系统偏差的在径向距、方位角和俯仰角范围rrange(i)、θrange(i)的上限和下限分别取整个仿真周期系统偏差模型的最大值和最小值，使之体现参数空间的广域性和可行性。为了与M-H算法进行比较，设置的相关参数为：阈值δ=0.4，Markov链长L=1 000，舍去预迭代值的个数为m=200；仿真采样100次；Monte Carlo次数为50次。算法运行硬件条件为Intel Core i7-2600 CPU 4 GHz。

3.1 参数估计性能仿真

图2为传感器A和传感器B在径向距和方位角上随机性系统偏差真实值且有突变发生。为了说明算法的有效性和可行性，图3和图4给出一次仿真得出的三种算法和真实系统偏差比较关系曲线图。由于随机性系统偏差难以建模，考虑充分利用传感器序贯量测的最大似然方法(简称ML)、Metropolis-Hasting(简称M-H)及本文提出的凸优化方法(简称Convex)进行对比。从图3和图4可以看出，相比于其他两种方法，Convex方法在径向距系统偏差估计效果较好；在方位角系统偏差估计效果，Convex方法要优于M-H方法且能估计出突变量，但是要逊于ML方法。原因在于系统偏差具有随机性和突变性，M-H和Convex两种方法在采样、学习过程中随机时变地在参数空间内游走，导致噪声存在时变方差，而ML方法的噪声满足某一近乎恒定方差，这在需要分辨率较高的方位角仿真图中能得到验证。

图5和图6为经过50次Monte Carlo仿真后三种算法关于传感器A和传感器B关于径向距、方位角的均方根误差比较图。从图5和图6可以看出，Convex方法在传感器A和B径向距的RMSE要好于M-H方法和ML方法；但传感器A和B方位角的RMSE，Convex方法基本上处于M-H方法和ML方法之间，分析可知Convex方法在方位角估计精度并没有定性于一定比M-H方法或ML方法中的任一种方法好。

图2 传感器A和B的系统偏差Fig.2 Systematic biases of the sensor A and B

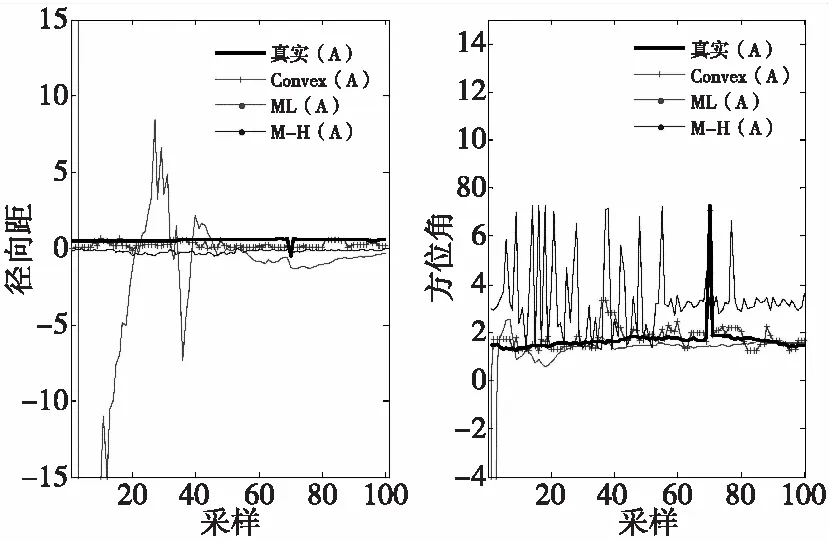
图3 传感器A的系统偏差估计比较图 Fig.3 Comparison of systematic bias estimation on sensor A

图4 传感器B的系统偏差估计比较图Fig.4 Comparison of systematic bias estimation on sensor B

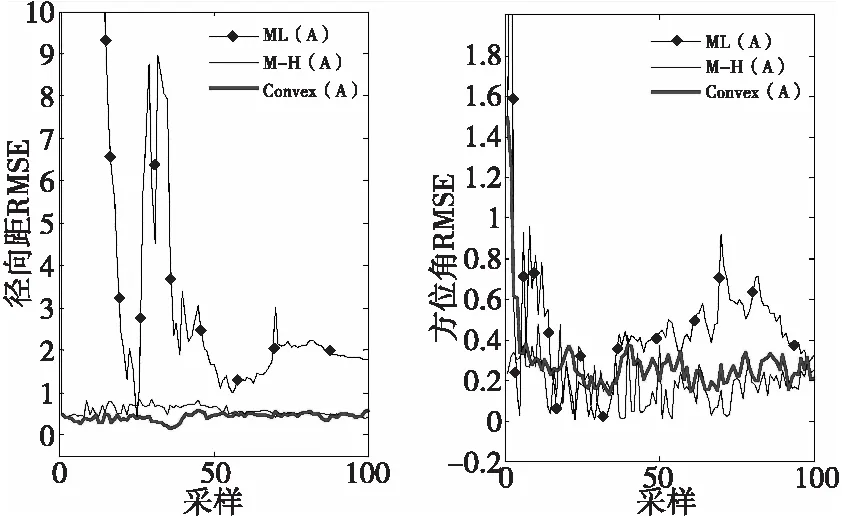
图5 传感器A的RMSE比较图Fig.5 Comparison of RMSE on sensor A

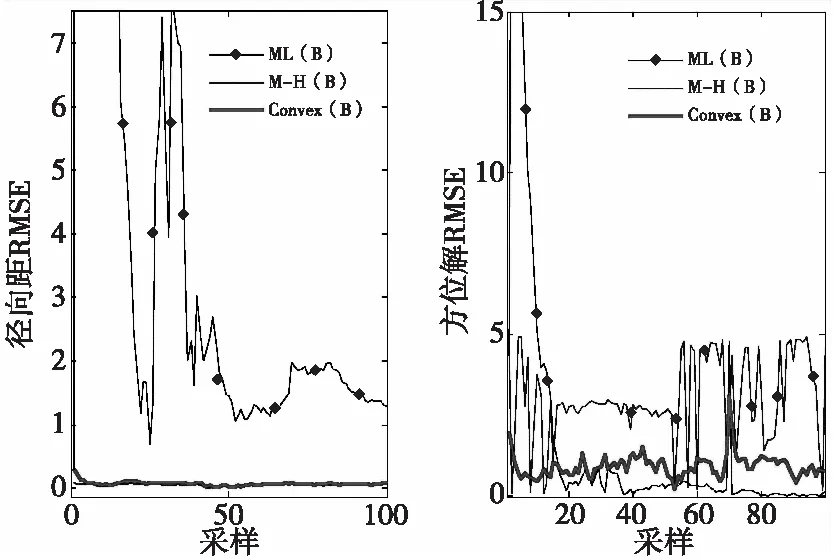
图6 传感器B的RMSE比较图Fig.6 Comparison of RMSE on sensor B

为了更直观地描述整个仿真过程的估计性能，表1给出经50次Monte Carlo仿真后三种算法估计出的传感器A和B在径向距和方位角系统偏差的平均均方误差。

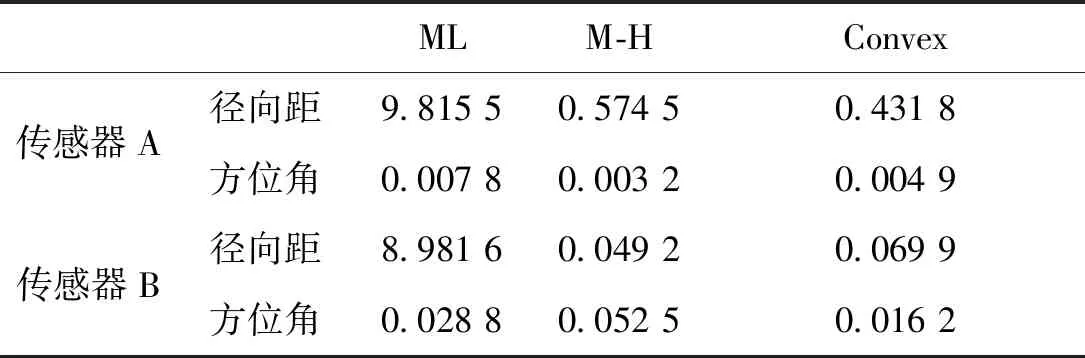
表1 三种算法的平均均方根误差

3.2 复杂度分析

为了验证Convex方法的实时性，经50次Monte Carlo仿真可知，三种算法的平均时间复杂度如表2所示。

分析原因，可依据ML、M-H及Convex算法的时间复杂度计算，其分别为O(n2·k)，O(L·n)，O(max{n3,n2·m,F})(其中，n表示系统状态维数，k表示第k次采样，L表示Markov链长，m表示约束不等式约束条件数目，F表示对所有不等式约束条件及其一阶、二阶导的计算代价)[17]。

表2 估计方法的平均运行时间

综合仿真曲线图和数据可知，在参数空间寻优求解范畴，Convex方法整体上比M-H方法耗时少、精度高；在整个仿真采样时间段的估计精度范畴，Convex方法比ML方法精度高。

4 结论

在贝叶斯估计框架下，本文充分利用多传感器的序贯量测信息，首先从量测最大似然函数入手，推算得到与状态参数无关的多传感器量测最大似然函数；然后将机动目标的系统模型从状态空间投影到系统偏差空间，并将投影表达式作为系统偏差二次函数的等式约束条件；随后，将待估的参数空间范围作为不等式约束条件，并联合等式约束条件，将最大似然估计问题转化为具有目标函数、约束函数的凸优化问题；最后利用凸优化工具包实现多传感器系统偏差的优化求解。本文新方法解决了当随机性的系统偏差难以建模时，传统估计方法带来的非全局最优解、非实时性等问题。