王瑞昌， 孙玉周

(中原工学院 建筑工程学院， 河南 郑州 450007)

近年来，各种特殊材料以及微/纳米量级新型构件被越来越多地应用到工程实际中，偶应力理论[1]和应变梯度理论[2]等高阶连续理论被广泛用在微/纳米结构或者需要考虑微尺度影响的宏观结构的研究中[3]。BORST等率先提出了基于Von-Mises屈服准则的Cosserat弹塑性理论[4]；FLECK等分别从统计存储位错和几何必需位错两个角度出发,改进了Cosserat弹塑性模型[5]；李锡夔等基于Drucker-Prager屈服准则给出了Cosserat弹塑性理论的塑性一致性算法[6]；冀宾等基于偶应力弹塑性理论，对软化行为的剪切带问题进行了有限元数值模拟[7]；张建成等利用非线性Cosserat扩展模型对层状岩体的洞室开挖过程进行了研究[8]。整体上说，由于数值离散时要求位移函数满足C1连续性，高阶连续理论、特别是高阶弹塑性理论的数值模拟仍然是工程数值仿真领域的研究热点。

无网格法是一种新型数值计算方法，与传统有限元法相比，具有形函数满足高阶连续特征、不受网格限制等特点，特别适合大变形、位移不连续、裂纹扩展和高速碰撞等问题的数值模拟[9]。本文尝试用无网格法建立基于偶应力理论的高阶弹塑性本构模型的数值计算框架 ，用Fortran语言编写计算程序，对悬臂梁进行数值模拟，以研究无网格法在高阶弹塑性问题数值模拟中的应用。

1 基于偶应力理论的高阶弹塑性本构模型

1.1 本构模型

偶应力理论的几何方程为

(1)

式中：εij为常规应变，ui、uj为位移，下标“，”表示对其后坐标求偏导，χij为微曲率，ωj为微转角。

增量形式的本构方程为

(2)

式(2)也可写为

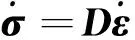
(3)

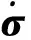
不记体力和体力偶时，平衡方程为

σij,j=0，mij,j+ejklσkl

(4)

式中：ejkl为排列算子。

静力边界条件为

(5)

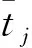
位移边界条件为

(6)

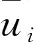
1.2 增量弹塑性阵

材料屈服后可把应变增量分为弹性增量和塑性增量两个部分，即

(7)

对于塑性变形而言，一应力增量可对应不同的塑性变形增量。根据相应的屈服准则和流动法则，可得

[D]ep=[D]e-[D]p=

(8)

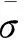
对于平面应力问题，应力增量和应变增量分别为

(9)

等效应力可通过应力偏量写为

(10)

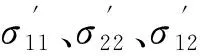
于是

(11)

偶应力理论的弹性矩阵为[10]

(12)

式中：E为弹性模量，v为泊松比。

将式(10)-式(12)代入式(8)并经过整理，最终得到平面应力问题的弹塑性阵显式表达式为

(13)

2 无网格法计算框架

控制方程的弱形式可写为

(14)

在无网格法中，域内任意一点x的位移增量可由移动最小二乘近似表示为[10-11]

(15)

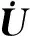
域内任意一点x处的应变增量可近似为

(16)

式中：B为几何矩阵，表达式如下

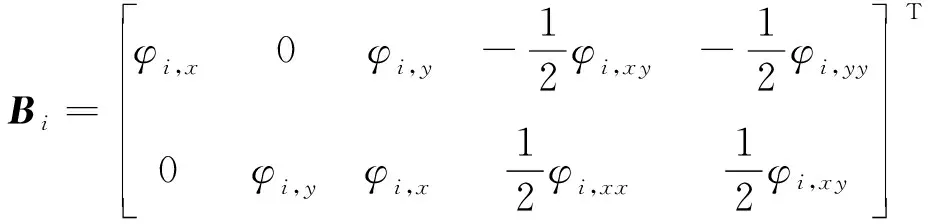
(17)

则域内任意一点x处的应力增量为

(18)

由式(14)可得离散控制方程为

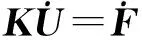
(19)

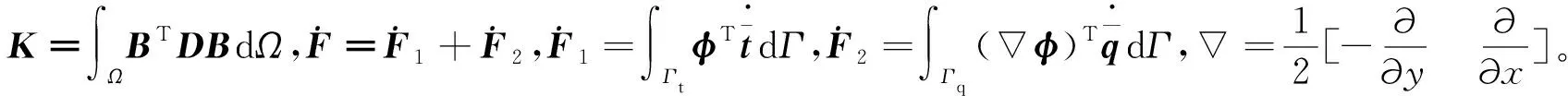
由于位移、转角和曲率均由节点位移来插值，位移和转角边界条件可采用罚数法施加。

3 数值算例及分析

图1所示为一端受集中力作用的悬臂梁，其几何尺寸取长度L=8.0 m,高度h=1.0 m，集中力F=1 N，弹性模量E=1.0×105Pa，泊松比v=0.25，屈服极限σs=25 Pa。采用线性强化弹塑性模型，H′=0.25E，切线模量E′=0.2E，材料服从Mises屈服条件。

图1 受集中力作用的悬臂梁模型

采用无网格法计算时，均布节点数为81×11，相邻节点间距在x和y方向上均为10 cm，背景网格数为80×10，与节点布置一致，背景网格内高斯点个数为3×3个。采用ANSYS建模时，节点及网格布置方案与无网格法相同，加载步数均为100。

表1给出了经典力学弹性解、ANSYS弹塑性解和本文方法(尺度因子l=0)计算得到的中性层各点挠度值。可以看出，无网格法计算结果与有限元软件ANSYS计算结果相差很小,且都大于经典力学弹性解。这说明本文建立的数值计算框架可以获得较好的效果。

图2所示为Von-Mises应力云图。当构件中某点的Mises应力超过屈服极限(σs=25 Pa)后即进入塑性阶段，从图中可明显观察到塑性区。

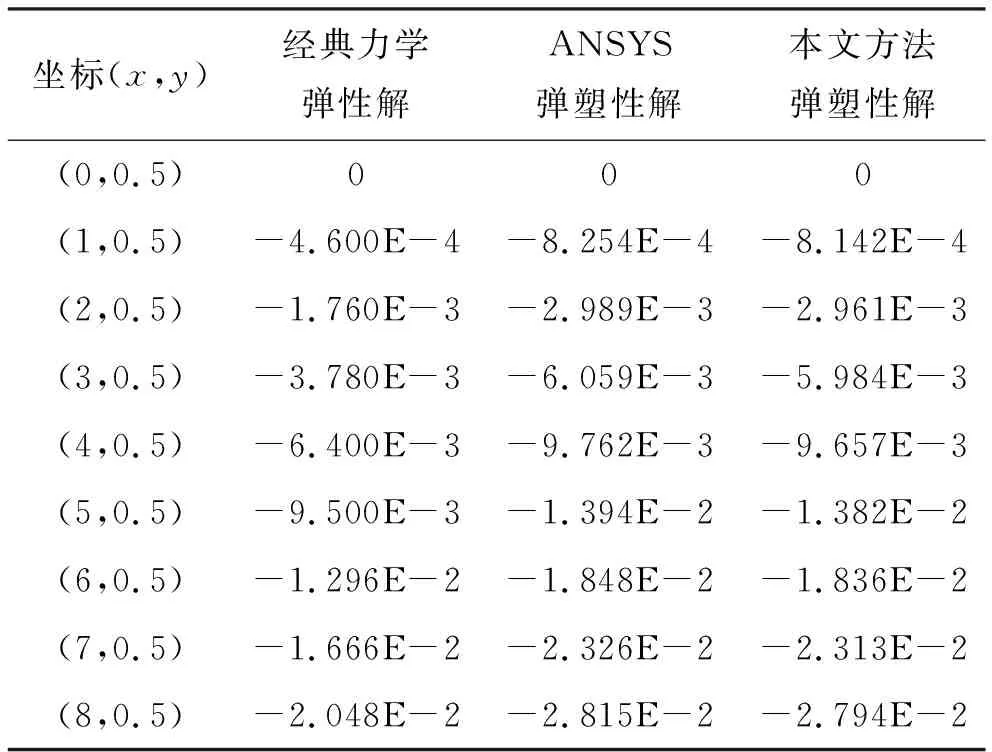
表1 一端受集中力作用的悬臂梁竖向位移 m

图2 无网格法数值模拟悬臂梁Von-mises应力云图

图3所示为悬臂梁右端中点的挠度与荷载的关系曲线图。从图中可以看出，在增量加载过程中，当荷载大于其弹性极限值(P>0.6 N)时，悬臂梁由弹性变形阶段进入塑性变形阶段。

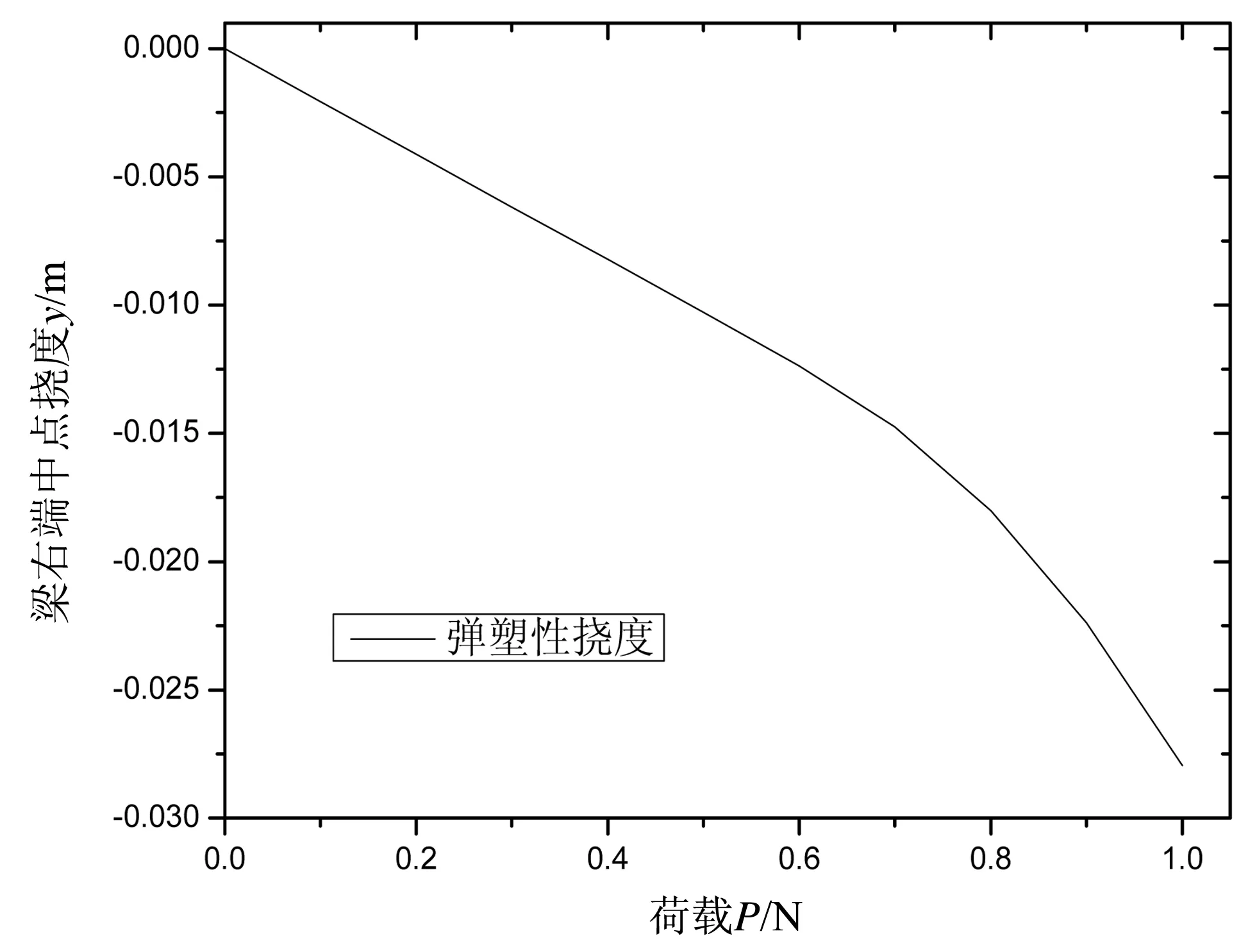
图3 梁右端中点的挠度与荷载的关系曲线图

为了分析尺度因子对悬臂梁弹塑性弯曲变形的影响，令尺度因子l在0～2.0b(b为厚度)之间变化，分别计算悬臂梁的中性层各点挠度值，并将其与有限元软件ANSYS计算结果进行比较，如图4所示。可以看出，当梁厚度远远大于材料的特征长度尺寸(如l<0.01b)时，梁的挠度曲线接近于ANSYS计算得到的弹塑性解，尺度效应可以忽略。随着材料特征长度尺寸的不断增大，由于存在偶应力，其弯曲刚度显著增加，对梁挠度的影响也随之增大。

图4 不同l/b条件下悬臂梁中性层挠度值

4 结语

本文以基于偶应力理论的高阶弹塑性本构模型为对象，建立了无网格法数值计算框架，用Fortran语言编写计算程序，并对悬臂梁的弹塑性弯曲变形进行了数值模拟，研究了无网格法在高阶弹塑性数值模拟中的应用。结果表明，本文方法不仅可以求解高阶弹性问题，对于高阶弹塑性问题也是非常有效的。当二维悬臂梁厚度接近材料特征长度尺寸时，由于存在偶应力，其弯曲刚度较之前有明显的增加，尺度效应较为明显；当其厚度远远大于材料的特征长度尺寸时，材料尺度效应非常弱，可以忽略不记。