陈圣兵　张浩　宋玉宝

摘要： 声子晶体具有弹性波带隙，可以用于结构振动与噪声控制。声子晶体传统能带算法一般给定波矢k在不可约布里渊区边界取值，然后求解特征频率ω，得到ω-k曲线。因而，传统方法中波矢k只取实数，只能求解实能带。为了求解复能带，一般需要给定频率ω，求解特征波矢k，从而得到k-ω曲线。提出了一种参数变换方法，解决了特征波矢求解中复杂的非线性特征值问题，实现了复能带的快速求解。最后，采用两个算例对文中算法进行了验证，包括布拉格声子晶体板和局域共振声子晶体板，研究了带隙内衰减常数随波传播方向的变化和阻尼对带隙的影响。

关键词： 声子晶体; 超材料; 复能带; 参数变换

中图分类号： O735; TB535  文献标志码： A  文章编号： 1004-4523（2019）03-0415-06

DOI：10.16385/j.cnki.issn.1004-4523.2019.03.005

引 言

声子晶体是由两种或两种以上介质组成的具有弹性波带隙的周期性复合材料或结构。当弹性波在声子晶体中传播时，某些频率范围内的弹性波传播将被抑制，相应的频率范围称为带隙。由于周期性结构广泛存在于实际工程结构中，人们对周期性结构的研究有着悠久的历史[1-3]。1992年，Sigalas和Economou研究了球形散射体埋入某一基体材料中形成的三维周期性复合介质中弹性波的传播特性，首次从理论上证实了三维周期点阵结构中存在弹性波带隙[4]。1993年，Kushwaha等在研究镍/铝二维固体周期复合介质时第一次提出了声子晶体的概念，类比光子晶体分析了声子完全带隙在理论研究中的意义[5]。1995年，Martínez-Sala等对西班牙马德里的一座具有两百多年历史的雕塑进行了声学特性测试，该雕塑是由直径为2.9 cm的中空不锈钢圆柱周期性排布在一个4 m直径的圆形平台上，形成的晶格常数为10 cm，通过测试他们第一次从实验角度证实了弹性波带隙的存在[6]。2000年，刘正猷等将包覆软硅橡胶材料的铅球按立方晶格嵌入环氧树脂基体中形成了一种三维三组元声子晶体，理论和实验结果均表明该声子晶体带隙所对应的波长远大于晶格常数，由此提出了局域共振声子晶体的概念[7]。近年来，局域共振声子晶体超常物理特性的揭示引起了学者的关注，并将这种具有超常物理特性的复合材料统称为超材料，其特性包括带隙、负折射、负模量和声学斗篷等[8-13]。

声子晶体传统能带算法一般将Bloch定理作为周期边界条件施加到求解域，先给定波矢k在不可约布里渊区边界取值，然后求解特征频率ω，从而得到能带曲线（ω-k）[14-16]。由于传统方法中波矢k只能取实数，所以这种求解方法存在一定的局限性，即只能得到实能带。但是为了研究带隙衰减能力，复能带的计算常常更有价值，不仅可以得到实能带，还可以得到带隙内衰减常数。尤其是引入阻尼后，通带内受到阻尼的耗散作用也会呈现一定的衰减，只有复能带能够很好地描述阻尼对带隙的影响。而反过来，如果给定频率ω，然后求解波矢k，就可以求解出复能带（k-ω）。但是，特征波矢k将出现在边界条件中，此时原问题变为非线性特征值问题，求解困难。这也是传统方法一般都是给定波矢，然后求解特征频率的原因。

为了能够计算声子晶体复能带，本文提出了一种参数变换方法，可以将周期边界条件中的未知波矢变换到偏微分方程的系数中，从而将原来复杂的非线性特征问题变换成线性特征值问题，能够实现复能带的快速求解。

3 算例与讨论

本文将采用两个算例来对文中算法进行验证，其中算例一为布拉格声子晶体板，算例二为局域共振声子晶体板，算例中所用到的材料参数如表1所示。

两个算例中，本文提出算法的理论计算都采用4节点Kirchhoff板单元，为了保证有限元计算结果收敛，分别对不同密度网格得到的结果进行了对比，结果表明采用12×12的网格已经能够得到收敛的计算结果。为了验证本文算法的正确性，还采用COMSOL软件计算了两个算例的实波矢，并与理论计算结果进行了对比。COMSOL软件中元胞建模为三维模型，网格划分采用二阶拉格朗日单元，同样对网格密度进行了分析，使得计算结果收敛。

3.1 布拉格声子晶体板

为了形成布拉格声子晶体板，基体材料选用环氧树脂，散射体为结构钢，材料参数如表1所示。晶格常数a=40 mm，散射体边长l=20 mm，板厚为h=3 mm。采用本文算法得到复能带如图3所示，并且采用COMSOL软件计算了该声子晶体的实波矢。从图中可以看出本文计算结果与COMSOL仿真结果符合的很好，但本文算法不仅可以計算实波矢，还可以计算波矢虚部从而得到带隙内衰减常数。在0-3000 Hz范围内，该声子晶体在ΓX方向形成了一个布拉格带隙（如图3（a）所示），而在ΓM方向没有产生带隙（如图3（b）所示），因此该带隙具有方向性。在ΓX方向，带隙内最大衰减常数约为δ=0.14，那么该频率的弯曲波经过一个周期传播后幅值衰减为e-0.14≈0.87。

为了研究带隙随方向的变化，计算了衰减常数随方向角θ的变化， 如图4所示。 从图中可以看出带隙宽度和带隙位置都随着方向而变化，带隙宽度随着角度θ的增大先减小后增大，带隙频率升高，而带隙内衰减也是先减小后增大。特别是在2200 Hz附近，方向带隙消失。

以1900 Hz为例，衰减常数随方向的变化如图5所示，从图中可以看出衰减常数在0°，±90°和180°方向最大（约为0.13），而在±45°和±135°方向衰减常数为零。因此，该频率的波在声子晶体中传播时具有明显的方向特性。

由于本文算法可以计算出复能带，所以可以用来分析阻尼对声子晶体带隙影响，这是传统实数能带无法描述的。在基体材料中引入结构阻尼系数η=0.01，计算得到复能带如图6所示。对比图3和6可以看出，阻尼对布拉格带隙的影响较小，尤其是实波矢基本没有变化。但通带内受到阻尼的影响，衰减不再为零，特别是带边附近出现了较强的阻尼衰减。

3.2 局域共振声子晶体板

为了形成二组元局域共振声子晶体板，基体材料选用结构钢，散射体选用较为柔软的橡胶，材料参数如表1所示。晶格常数为a=40 mm，散射体边长为l=30 mm，板厚为h=3 mm。计算得到复能带如图7所示，同样利用COMSOL软件计算了该声子晶体的实波矢。从图中可以看出本文计算结果与COMSOL仿真结果也符合的很好，但本文方法同样能够给出局域共振带隙内衰减常数。在0-200 Hz范围内，该局域共振声子晶体产生了一个局域共振带隙。对比图7（a）和（b）可以看出，该带隙频率范围在ΓX方向和ΓM方向基本一致，证明该带隙为一个完全带隙，但从衰减常数可以看出，带隙内衰减在这个两个方向并不相同。可以看出，ΓX方向的带隙内衰减要大于ΓM方向的带隙内衰减，但衰减常数都是在接近下带边的频率附近达到最大。

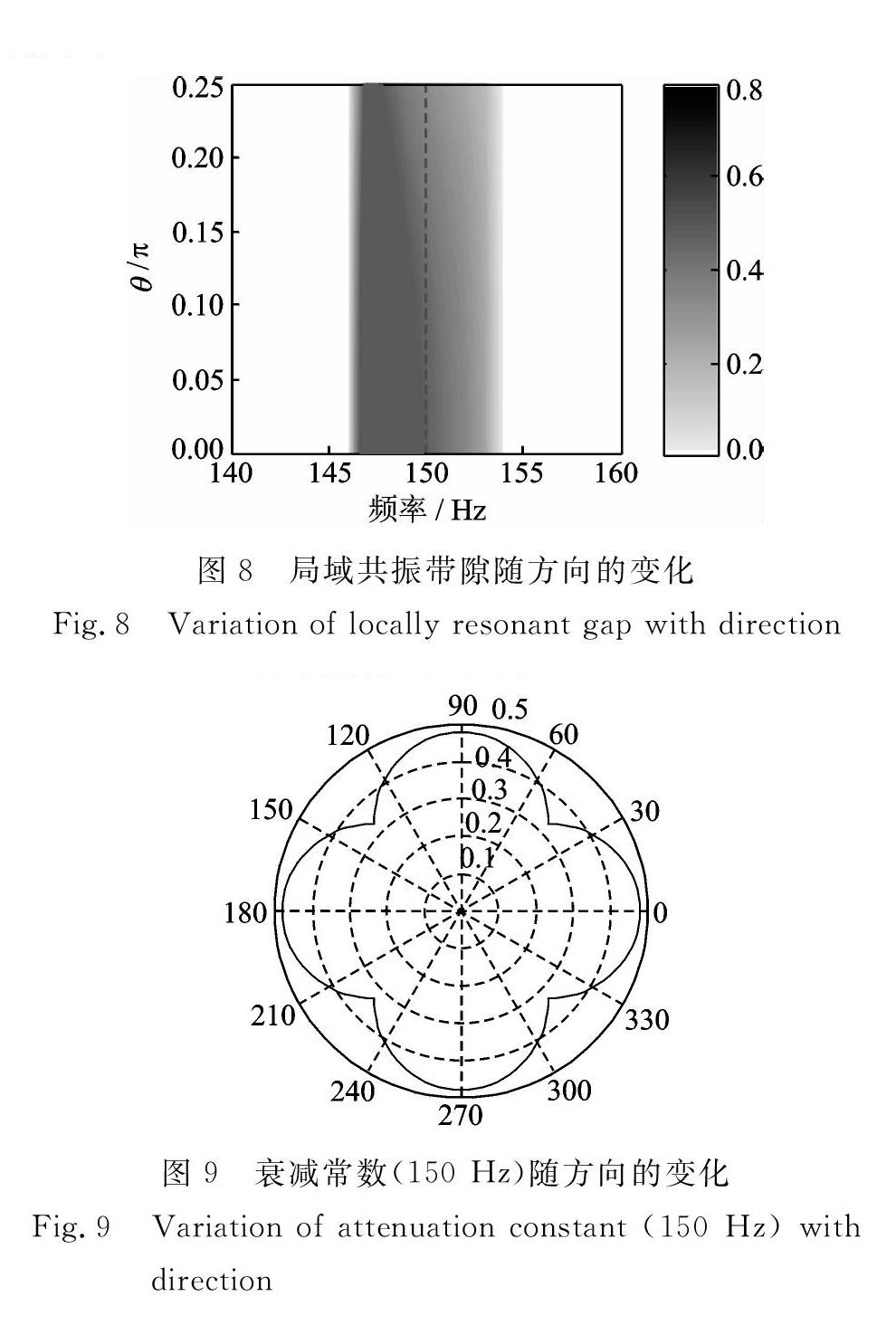
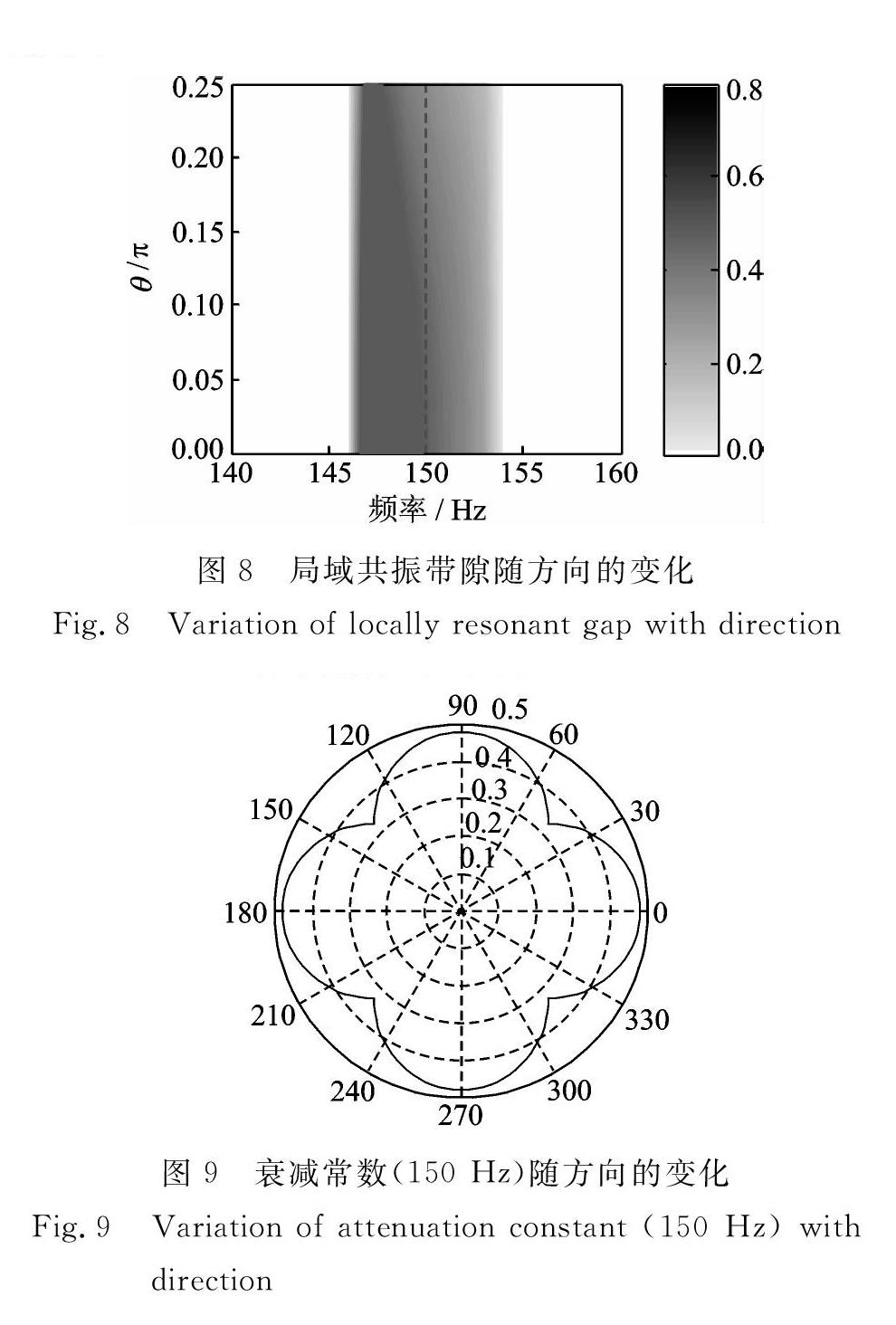
同样，为了研究带隙随方向的变化，计算了衰减常数随方向角θ的变化，如图8所示。从图中可以看出带隙宽度和带隙位置不随方向变化，但带隙内衰减随着角度θ的增大而减小，在45°方向达到最小。

以150 Hz为例，衰减常数随方向的变化如图9所示，从图中可以看出衰减常数在0°，±90°和180°方向最大（约为0.48），而在±45°和±135°最小（约为0.23）。那么150 Hz的波传播一个周期后，在0°，±90°和180°方向幅值衰减为e-0.48≈0.62，而在±45°和±135°方向幅值衰减为e-0.23≈0.79。

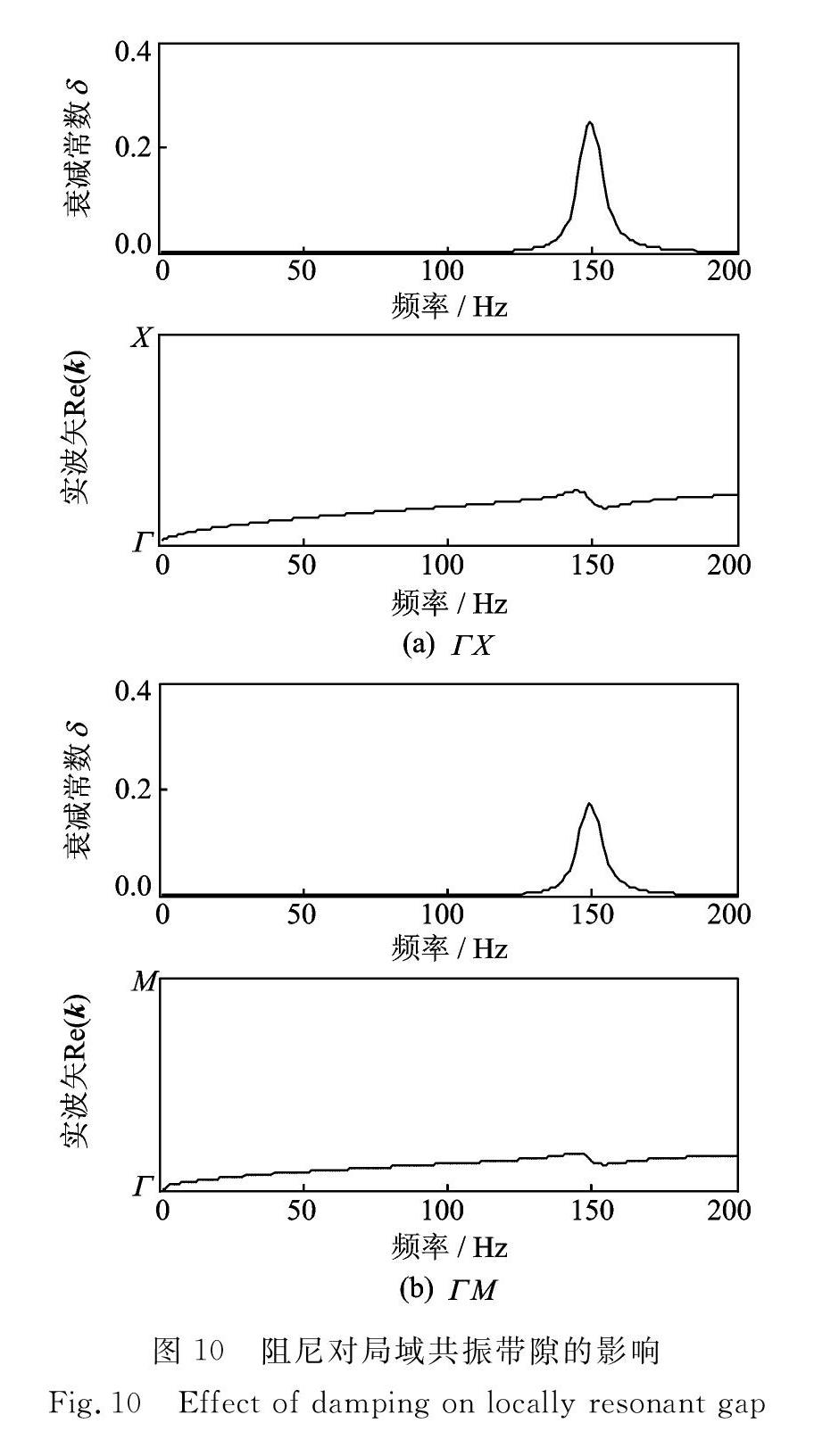
为了分析阻尼对声子晶体局域共振带隙影响，在散射体中引入结构阻尼系数η=0.05，计算得到复能带如图10所示。对比图7和10可以看出，增加阻尼后带隙内波矢不再为纯虚数，而带隙外较大频率范围内波矢也不再为纯实数，即带隙内外较大范围都将是复数，只有复能带能很好地进行描述。阻尼使得带隙内衰减减小，但带边附近却出现了较强的阻尼衰减，证明引入适当的阻尼可以增大带隙的衰减带宽。与布拉格带隙不同，阻尼对实波矢的影响很大，抑制了实波矢在带隙附近的剧烈变化。

可以看出，阻尼对局域共振带隙的影响远大于布拉格带隙，这是由两种带隙的形成机理决定的。布拉格声子晶体板的基体和散射体材料参数相差较小，因而带隙内振动能量在整个元胞内分布，基体阻尼只对部分机械能形成耗散;局域共振声子晶体板的基体和散射体材料参数相差较大，因而带隙内振动能量基本都被局域在散射体内，散射體阻尼将对几乎全部机械能形成耗散，其带隙内阻尼效果要远比布拉格声子晶体强。

4 结 论

本文提出了一种参数变换方法，解决了特征波矢求解中复杂的非线性特征问题，实现了复能带的快速求解。文中通过两个算例对算法进行了验证，分别为布拉格声子晶体板和局域共振声子晶体板。布拉格声子晶体板在0-3000 Hz内产生了一个布拉格带隙，该带隙具有方向性，在ΓX方向存在较大衰减，但在ΓM无衰减。基体阻尼对布拉格带隙影响较小，但在带边处产生了显著的阻尼衰减，扩大了带隙的衰减范围。局域共振声子晶体在0-200 Hz内产生了一个局域共振带隙，该带隙为完全带隙，但带隙内衰减在不同方向稍有不同。散射体阻尼对局域共振带隙影响显著，带隙内衰减减小，但带边处阻尼衰减较大。本文参数变换方法不限于声子晶体板，也可推广于其他二维和三维声子晶体复能带的计算。

参考文献：

[1] Mead D J. Free wave propagation in periodic-supported，infinite beams[J].Journal of Sound and Vibration， 1970， 11（2）： 181-197.

[2] Mead D J， Markus S. Coupled flexural-longitudinal wave motion in a periodic beam[J]. Journal of Sound Vibration， 1983， 90（1）： 1-24.

[3] Mead D J. A new method of analyzing wave propagation in periodic structures： Applications to periodic Timoshenko beams and stiffened plates[J]. Journal of Sound Vibration， 1986， 104（1）： 9-27.

[4] Sigalas M M， Economou E N. Elastic and acoustic wave band structure[J]. Journal of Sound Vibration， 1992， 158（2）： 377-382.

[5] Kushwaha M S， Halevi P， Dobrzynski L， et al. Acoustic band structure of periodic elastic composites[J]. Physics Review Letter，1993，71（13）： 2022-2025.

[6] Martinez-Salar R， Sancho J， Sanchez J V， et al. Sound attenuation by sculpture[J]. Nature， 1995，378（6554）： 241.

[7] Liu Z Y， Zhang X， Mao Y， et al. Locally resonant sonic materials[J]. Science， 2000，289（5485）： 1734-1736.

[8] Li J， Chan C T. Double-negative acoustic metamaterial[J]. Physics Review E， 2004， 70（5）： 055602

[9] Fang N， Xi D， Xu J， et al. Ultrasonic metamaterials with negative modulus[J]. Nature Materials， 2006， 5（6）： 452-456.

[10] Milton G W. New metamaterials with macroscopic behavior outside that of continuum elastodynamics[J]. New Journal of Physics， 2007， 9（39）： 46-50.

[11] Li Y F， Meng F， Li S， et al. Designing broad phononic band gaps for in-plane modes[J]. Physics Letters A， 2018， 382（10）： 679-684.

[12] Srivastava A， Lu Y. Variational methods for phononic calculations[J]. Wave Motion， 2016， 60： 46-61.

[13] Coffy E， Euphrasie S， Addouche M， et al. Evidence of a broadband gap in a phononic crystal strip[J]. Ultrasonics， 2017， 78： 51-56.

[14] Chen S B， Wen J H， Wang G， et al. Tunable band gaps in acoustic metamaterials with periodic arrays of resonant shunted piezos[J]. Chinese Physics B， 2013， 22（7）： 074301.

[15] Yu D L， Wang G， Liu Y Z， et al. Flexural vibration band gaps in thin plates with two-dimensional binary locally resonant structures[J]. Chinese Physics， 2006， 15（2）： 266-271.

[16] Xiao Y， Wen J， Wen X. Flexural wave band gaps in locally resonant thin plates with periodically attached spring-mass resonators[J]. Journal of Physics D： Applied Physics， 2012， 45（19）： 195401.

Abstract： Phononic crystals possess elastic wave band-gaps， which can be used to control the vibration and noise of structures. To obtain the band structures of the phononic crystals， the conventional procedures are as follows： given the wave vector k， whose value sweep the boundary of Brillouin zone， the eigenfrequency ω can be evaluated， resulting in the ω-k curve. However， this method can only yield the real band structure. In order to get the complex band structure， the frequency ω usually is given and then the eigenvalue of wave vector k is calculated， resulting in the k-ω curve. This work proposes a parameter transformation method， which can resolve the complicated non-linear eigenvalue problem and achieve the rapid solution of complex band structure. Finally， two examples， i.e.， a Bragg phononic plate and a locally resonant phononic plate， are adopted to validate the proposed method. The variation of the attenuation constant along with the wave direction in the band gap and the influence of damping on the band gap are investigated in detail.

Key words： phononic crystals; metamaterials; complex band structure; parameter transformation

作者簡介： 陈圣兵（1984-），男，助理研究员。电话： （0816）2465610;E-mail：nudt_chen@163.com