Pradnya N.P.Ghoderao,Vishwanath H.Dalvi*,Mohan Narayan

1 Department of Physics,Institute of Chemical Technology,Mumbai 400019,India

2 Department of Chemical Engineering,Institute of Chemical Technology,Mumbai 400019,India

Keywords:Phase equilibria Thermodynamic properties Vapor-liquid equilibria The cubic equation of state Covolume parameter Supercritical region

ABSTRACT A four-parameter,Ghoderao-Dalvi-Narayan 2 cubic equation of state(GDN2 CEOS),is presented which incorporates the following:1.The experimental value of the critical compressibility factor has been used as a fixed input parameter for calculations;2.All the parameters(a,b,c,d)of CEOS are temperature dependent functions in the subcritical region and are temperature independent functions in the supercritical region and;3.A new α function is introduced with two compound specific parameters which are estimated by matching saturated vapor pressure at two fixed temperature points Tr=0.5, 0.7.Our formalism enables us to cast three of the four parameters of the CEOS as a function of the remaining parameter.The proposed CEOS is used to predict properties of 334 pure compounds,including saturated vapor pressure and liquid density,compressed liquid density,heat capacities at the constant pressure and volume,enthalpy of vaporization,sound velocity.To calculate thermodynamic properties of a pure compound,the present CEOS require the critical temperature,the critical pressure,the Pitzer's acentric factor,the critical compressibility factor,and two parameters of the alpha function.The saturated liquid density predictions for pure fluids are very accurate when compared with GDN1(Ghoderao-Dalvi-Narayan 1),MPR(Modified Peng-Robinson),and PT(Patel-Teja)equations of state.Unlike MPR EOS,the proposed temperature dependent covolume parameter b in the present work satisfies all the constraints mentioned in the literature to avoid thermodynamic inconsistencies at the extreme temperature and pressure.Using van der Waals one-fluid mixing rule,the present CEOS is further used to predict bubble pressure and the vapor mole fraction of binary mixtures.

1.Introduction

The equation of state(EOS)is a very important tool for the prediction of thermodynamic properties and phase equilibria of pure fluids and mixtures.Generally,EOS can be categorized into three types according to their fundamentals:empirical,theoretical and semiempirical[1].The cubic equation of state(CEOS)is semi-empirical,closed form and its cubic nature allows great facilities in numerical calculations[2]and hence is extensively used for thermodynamic properties predictions.The CEOS framework,first proposed by van der Waals [3],has been remarkably successful for correlating thermodynamic properties of simple fluids,especially in the prediction of vapor-liquid equilibria.This CEOS has been modified in several ways to improve thermodynamic property predictions[4-8].The best known of the modifications are the Soave-Redlich-Kwong[9](SRK)and Peng-Robinson[10](PR)equations of state(EOSs)which are extensively used for process engineering calculations.While extremely successful in predicting saturation vapor pressures, these “two-parameter” CEOS fail to accurately predict liquid densities accurately.This shortcoming has been remedied to a large extent by adding a third parameter:either as a volume correction which is called as “volume-translated” EOS [11-17] or to form“three-parameter”CEOS,the most notable of which is the Patel-Teja[18](PT)EOS.

In the case of three parameter EOSs,the critical compressibility factor is not a universal number but taken as an adjustable parameter which results in an improved performance for liquid density when compared with two parameter EOSs. However,three parameter EOSs always overestimate the critical compressibility factor [19-21] and liquid density predictions are not improved for polar compounds.Hence,to overcome shortcomings of two and three parameter EOSs,the four parameter EOS is a natural extension and allows critical compressibility to be set to its experimental value with the additional parameter used for fitting.The literature survey[5,22,23]indicates that four parameter EOSs are not very well studied. The four parameter EOS was first proposed by Adachi et al.[5]in 1983 with the following findings:the complicated repulsive term has no real advantage over widely used van der Waals repulsive term except in the saturated liquid density which is mainly controlled by a repulsive term of the EOS.Trebble and Bishnoi[22]in 1987 have presented a four parameter EOS which was modified by Salim and Trebble(TBS)[24]in 1991.The generalized TBS EOS predicted PVT data with remarkable accuracy when compared with other contemporary EOSs and concluded that temperature dependent covolume parameter(b)led to negative isochoric heat capacity at extreme conditions. Jan and Tsai [23] in 1991 reported a four parameter EOS and claimed that this equation predicts saturated liquid density precisely when compared to contemporary EOSs.Ghoderao et al.[25]in 2018 presented a four parameter EOS(GDN1)with critical compressibility factor taken as an experimentally given input parameter and obtained very accurate predictions for saturation properties.The GDN1 was further extended to binary mixtures using van der Waals one-fluid mixing rules.The authors claimed that the advantage of using four parameter CEOS is that the extra fourth parameter can be used as an adjustable parameter retaining the critical compressibility factor as an experimentally given input parameter which gives exact critical point of any substance.

Kinetic theory of gases [3,26] suggests that the parameter b should be a function of temperature,it has been taken as a temperature dependent parameter in recent studies [27-29]. Salim and Trebble [24] have stated two constraints on temperature dependence in b: 1. The first derivative of b with respect to temperature must be positive to avoid isotherms crossover at high pressure. 2.The second derivative of b with respect to temperature must be negative to avoid large negative values of the isobaric heat capacity at high pressure.From literature survey,we have observed that,temperature dependent covolume parameter proposed in most of the previous works do not satisfy above mentioned constraints simultaneously.In our work,a new temperature dependent function for the covolume parameter b is introduced;which is temperature dependent in the subcritical region and temperature independent in the supercritical region. It satisfies above mentioned constraints to avoid thermodynamic inconsistencies at high temperature and high pressure.The purpose of this work was to ascertain whether a temperature dependence in the co-volume parameter would significantly improve predictive abilities of a cubic EOS.Very few papers have addressed this particular issue and we thought it interesting to explore.

We have developed a new formalism in which three of the four parameters (a,c,d) are cast as a function of covolume parameter(b)and the introduction of temperature dependence in b results in the temperature dependence in all parameters in the subcritical region. Unlike most of the previous work [18],the critical compressibility factor is taken as experimentally given input parameter.The alpha function α(T) and covolume parameter (b) of GDN2 EOS are estimated to get an accurate representation of saturated vapor pressure and liquid density.According to Duan et al.[30],a generalized alpha function does not yield a precise description of vapor pressures of strongly polar fluids and weakly polar fluids with small Zcover the whole vapor-liquid equilibrium curve.Hence,we have introduced two compound specific parameters in the alpha function which can be obtained by matching saturated vapor pressure data at two reduced temperature points Tr=0.5,0.7.

Using the present CEOS,we have calculated various thermodynamic properties of pure fluids including saturated liquid density and vapor pressure,compressed liquid density,heat capacity at constant pressure and volume,enthalpy of vaporization,sound velocity in the supercritical region.Additional quantities like bubble pressure and the vapor mole fraction are predicted for binary mixtures.The results obtained using our CEOS are compared with those obtained using GDN1(Ghoderao-Dalvi-Narayan 1), MPR [28] (Modified Peng-Robinson), and PT(Patel-Teja) equations of state. Recently, Forero and Velásquez [31]have presented modified Patel-Teja equation(MPT)of state to predict saturation properties of polar substances accurately and further extended to mixtures.We have considered 15 polar compounds and compared our results with that of MPT EOS.

Phase equilibrium calculations constitute the innermost iterative loop of process calculations.Historically,cubic equations of state,afford rapid and accurate solutions[32,33].However,increasing the accuracy of the CEOS has important implications for developing better process simulators.

2.Theory

The CEOS adopted in this work is[34]:

where a,b,c and d are constants and α is a temperature dependent function which must satisfy following properties[35,36]:

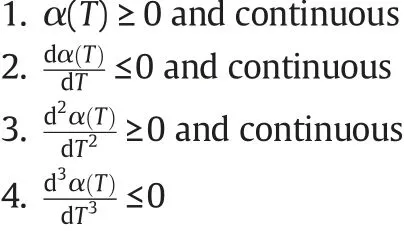
The PR EOS results from setting c=d=b in Eq.(1);the SRK by setting c=0 and d=b;the PT EOS is recovered by setting d=b.

Generally,to ensure an inflection in the P vs v curve at the critical point,these constants are written as:

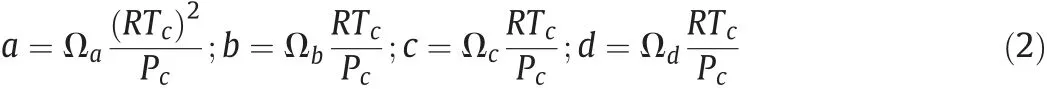
The proportionality constants in Eq.(2)are traditionally been defined as Ωa,Ωb,Ωcand Ωdrespectively.

There are two conditions(besides the fact that α(Tc)=1)that must be fulfilled at the critical point,namely:

For two-parameter cubic equations of state such as SRK and PR,parameters a and b are determined by using the two conditions stated in Eq.(3),whereas for the three-parameter EOS,an additional condition is needed.

Eq.(3)is equivalent to stating that the following cubic equation has three equal roots at T=Tc.

where,Z=Pv/RT is the compressibility factor.The above Eq.(4)is derived by setting v=ZRT/P in Eq.(1)and rearranging in the form of a polynomial in Z.The coefficients AZ,BZ,and CZare given as:

Substituting T=Tcand P=Pcin the Eqs.(5),(6)and(7)and using the definitions of a,b,c,d from Eq.(2)and noting that α(Tc)=1 we have:

In the case of the“two-parameter” CEOS(SRK andPR),Zcis set constant for all fluids, For SRK,=and =0 and Eq.(8)results in=13,Eqs.(9)and(10)results in=1）and=19（213-1）-1.Similarly,for PR,Eqs.(8),(9)and(10)results in ZcPR=0.3074, ΩbPR=0.077796 and ΩaPR=0.457235 [37]. Since Zcvalues for most industrially important compounds are somewhere between 0.2 and 0.3,the two-parameter EOS state consistently over-predict liquid volumes.An important part of the great appeal of the twoparameter cubic equations of state for process calculations is the universality of the constants Ωaand Ωbat the expense of an error in liquid volume.Eqs.(8)and(9)can be written as,

Eqs.(11)and(12)are the two equations for Ωcand Ωawhich are explicit in Ωband Eq.(13)is a single cubic equation in Ωb.

However,an examination of Eq.(13)suggests a simple rearrangement to get a quadratic in Ωdwith two roots:

Substituting Eq.(14)in Eq.(11),we obtained two values for Ωccorresponding to each Ωd.

We observed that both Ωcand Ωdappear in subsequent equations only in Ωc+Ωdor ΩcΩdform.If we look at Eqs.(14)and(15)carefully,we see that both values of Ωdwith respective Ωcwill give us the same values of Ωc+Ωdand ΩcΩd.Hence,we can select any one root of Eq.(14)for further calculations.

Here,Δbis given as:

From Eqs.(13),(14),and(15),we can see that all parameters Ωa,Ωdand Ωcare explicit functions of Ωb.

In present approach, the experimental critical compressibility factor is used for calculations, whereas in MPR, PT, and other twoand three-parameter EOSs, the critical compressibility factor is an adjustable parameter obtained by minimizing following objective function(OF):

Here,the weight factors w1and w2are fixed according to the EOS and np is the number of experimental data points.

3.Methodology

The Ghoderao, Dalvi, Narayan (GDN2) EOS is a four-parameter CEOS and has the form as given in Eq.(1). The values of Ωb(T) and α(T)are obtained by minimizingrespectively at each temperature T using the least square method in Python 2.7.10.

The minimization process is as follows:Ωbis obtained by an iterative procedure where Ωbis first guessed and substituted into Eqs.(12), (14) and (15) to get Ωa,Ωdand Ωcrespectively which are then used in an iterative loop to obtain the value of α at which the value ofis minimum at given Trotherwise the guess of α is refined. With known Ω′s, α and pcal, if the corresponding liquid volume does not match the value from the empirical correlation i.e.the value of）is not minimized with the desired accuracy,the guess of Ωbis refined.A Flowchart to illustrate above mentioned procedure is shown in Fig.1.

Fig.1.Flowchart to determine α and Ωb using CEOS.

We found that Ωbwith the following functional form,with A,B,C specified as given below gives best fit to the Ωbobtained by the procedure outlined above.

Tr=T/Tcis the reduced temperature and A,B,C are given below:

Similarly,α with the following functional form with two compound specific parameters m and n gives the best fit to the α obtained by the above iterative method.

The variation of the alpha function with temperature for dodecane,ethane and carbon dioxide is shown in Fig.2.

Fig.2.Variation of the alpha function with respect to reduced temperatur e.

To determine parameters m and n in Eq.(18),we need to know experimental saturated vapor pressure at only two points i.e.at fixed reduced temperatures 0.5 and 0.7 and minimize the following objective function using the least square method in Python 2.7.10.

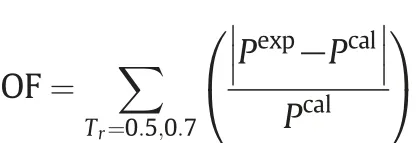
It has been observed that the Eq.(16)shows a sharp decrease in the supercritical region which results in unphysical property predictions.Hence,we have proposed temperature independent Ωbin the supercritical region.

The temperature dependent covolume parameter b leads to thermodynamic inconsistencies such as negative isobaric and isochoric heat capacities and in some cases intersection of isotherms at elevated pressure [38-40]. Hence, to avoid these inconsistencies, Salim and Trebble [24] have stated constraints on temperature dependence in b which we have discussed in the Introduction section.The Ωbproposed in the present work [Eq.(16)and(19)]satisfies these constraints and hence,does not encounter with any inconsistencies.

4.Results and Discussion

The goal of a CEOS is to predict thermodynamic properties, of which vapor pressure and saturation liquid density are the most important properties. However, CEOS is further used to calculate properties such as the enthalpy of vaporization, the isobaric and isochoric heat capacities,the sound velocity,the compressed liquid density of pure compounds and the bubble point pressure, the vapor mole fraction of binary mixtures. The critical temperature,critical pressure,critical compressibility factor,acentric factor and component specific parameters m and n required for calculations are given in Table 1 for 334 components. In Table 2, the saturated vapor pressure and liquid density of pure compounds obtained from GDN2 EOS are compared with GDN1, MPR, and PT EOSs. The mean of percentage average absolute deviation1MAAD （%）=N:Number of the data points refers to number of temperatures at which above properties are given;Y:some thermodynamic property(MAAD) of the saturation vapor pressure for 56 pure compounds fitted by GDN2 EOS is 1.69%, whereas it is 1.54%, 2.02% and 2.73% for GDN1, MPR,and PT EOSs respectively. Among 56 compounds, GDN2 EOS predicts saturation liquid density better than GDN1, MPR, and PT EOSs for all compounds i.e. AAD (average absolute deviation) of the liquid density fitted by GDN2 EOS is 3.62%,whereas it is 4.36%,5.66%and 5.16%for GDN1,MPR,and PT EOSs respectively.The pressure-density plot for different compounds calculated using GDN2 and MPR EOSs is shown in Fig.3.It can be seen that the GDN2 EOS predicts density with far better accuracy when compared with the MPR EOS.Figs.4,5,6 and 7 are temperature-density plot at various pressures for methane, ethane, carbon dioxide and nitrogen respectively.It is seen that all EOSs that fit the phase envelope well,deviate significantly at high pressures. The common denominator in both cases is the high density.Hence it points to a lacuna in the repulsive term since it is this term that dominates at high densities.It appears that there is a room for improvement in the repulsive term of the CEOSs since a good fit to one high-density region(subcritical liquid phase)results in a poor fit in another high density region (supercritical phase). However, even here, the GDN2 shows better behavior than MPR EOS.Like GDN2 EOS,MPR EOS also uses temperature dependent covolume parameter b but it sharply decreases at high temperature which leads to unphysical property prediction at high temperature.In Fig.7,the MPR EOS predicts negative values for density,hence not shown.

The enthalpy of vaporization and compressed liquid density are demonstrated in Table 3.MAAD of the enthalpy of vaporization for 48 compounds is 3.75%, 3.56%, 4.80%, and 4.87% for GDN2, GDN1, MPR,and PT EOSs. Fig. 8 shows a plot of the enthalpy of vaporization (h)against temperature plotted for different compounds like ammonia,argon,phenol,carbon disulfide and water.The predicted enthalpy of vaporization is in good agreement with the experimental.MAAD of the compressed liquid density for 31 compounds is 3.93%, 3.99%, 5.80%,and 4.18% for GDN2, GDN1, MPR, and PT EOSs. The ability of GDN2 EOS to represent polar substance saturation properties like saturated vapor pressure,liquid density and enthalpy of vaporization accurately is evaluated by comparing results with that of MPT EOS[31]as shown in Table 4.We have considered 15 polar compounds and results show that MPT EOS is performing better in the prediction of liquid density but GDN2 EOS performs better for vapor pressure and enthalpy of vaporization prediction.

Fig.9 shows the plot of isobaric heat capacity(Cp)calculated using GDN2 EOS against temperature for ethane at different pressures whereas the variation of isochoric heat capacity(Cv)for various compounds like nitrogen, methane, oxygen, ethane and, argon with the temperature at 10 MPa pressure is shown in Fig.10.The GDN2 EOS is further used for calculation of sound velocity.In Fig.11,we show the sound velocity(vs) as a function of temperature at 10 MPa pressure for the compounds including nitrogen,carbon dioxide,hydrogen sulfide,nitrogen trifluoride and neon.The relations required for calculation of above thermodynamic properties are given in Appendix A.

5.Application of GDN2 EOS to Mixtures

We now apply GDN2 EOS to mixtures and calculate the bubble pressure and vapor phase mole fractions of various mixtures. In thesecalculations,we have used van der Waals one-fluid mixing rules.These rules are given below[43]:

Table 1 The pure components with properties like critical temperature,critical pressure,critical compressibility factor,acentric factor and are taken from Perry's chemical engineers'handbook[42].m and n are parameters of the alpha function in Eq.(18)

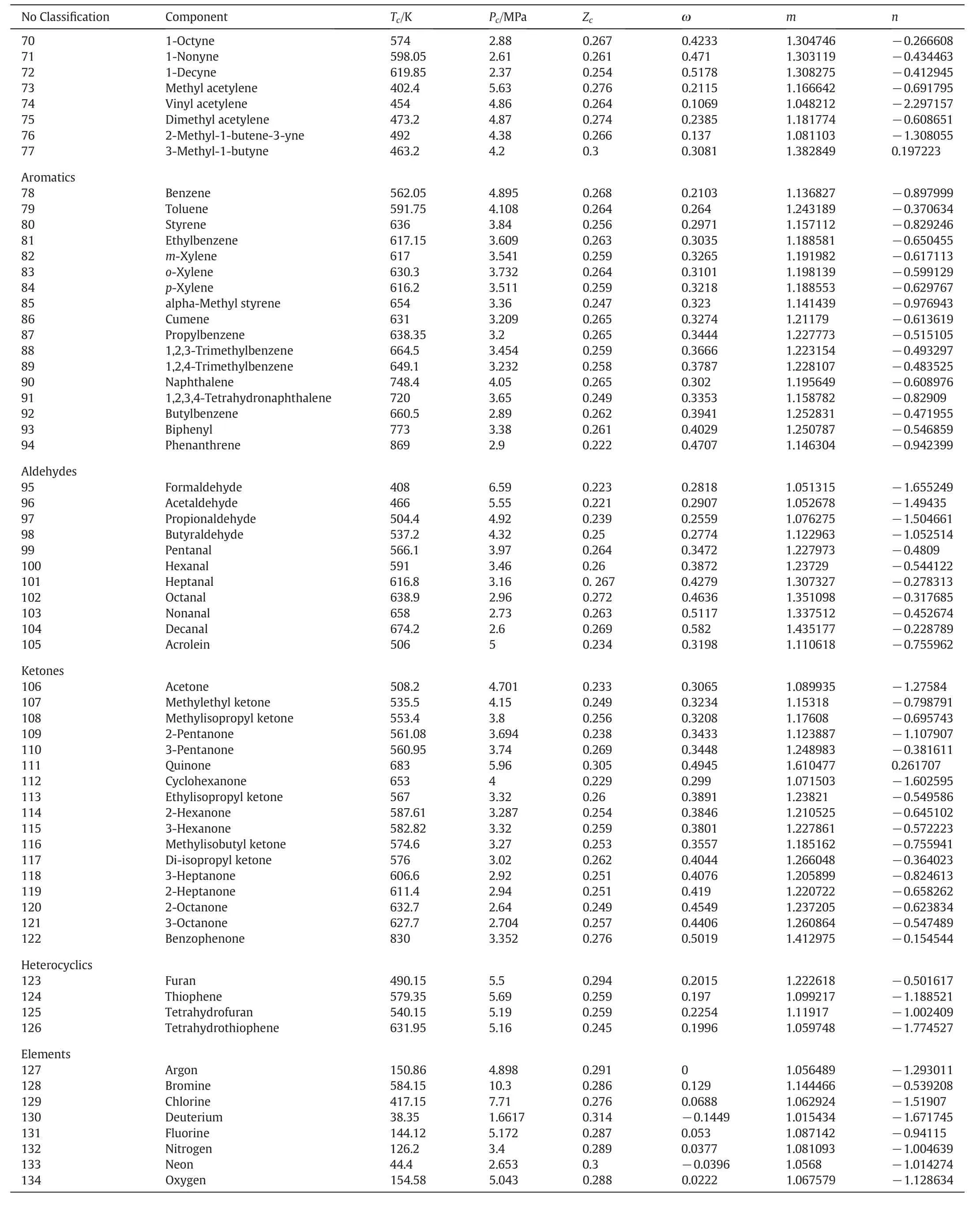
Table 1(continued)

Table 1(continued)

Table 1(continued)

(continued on next page)

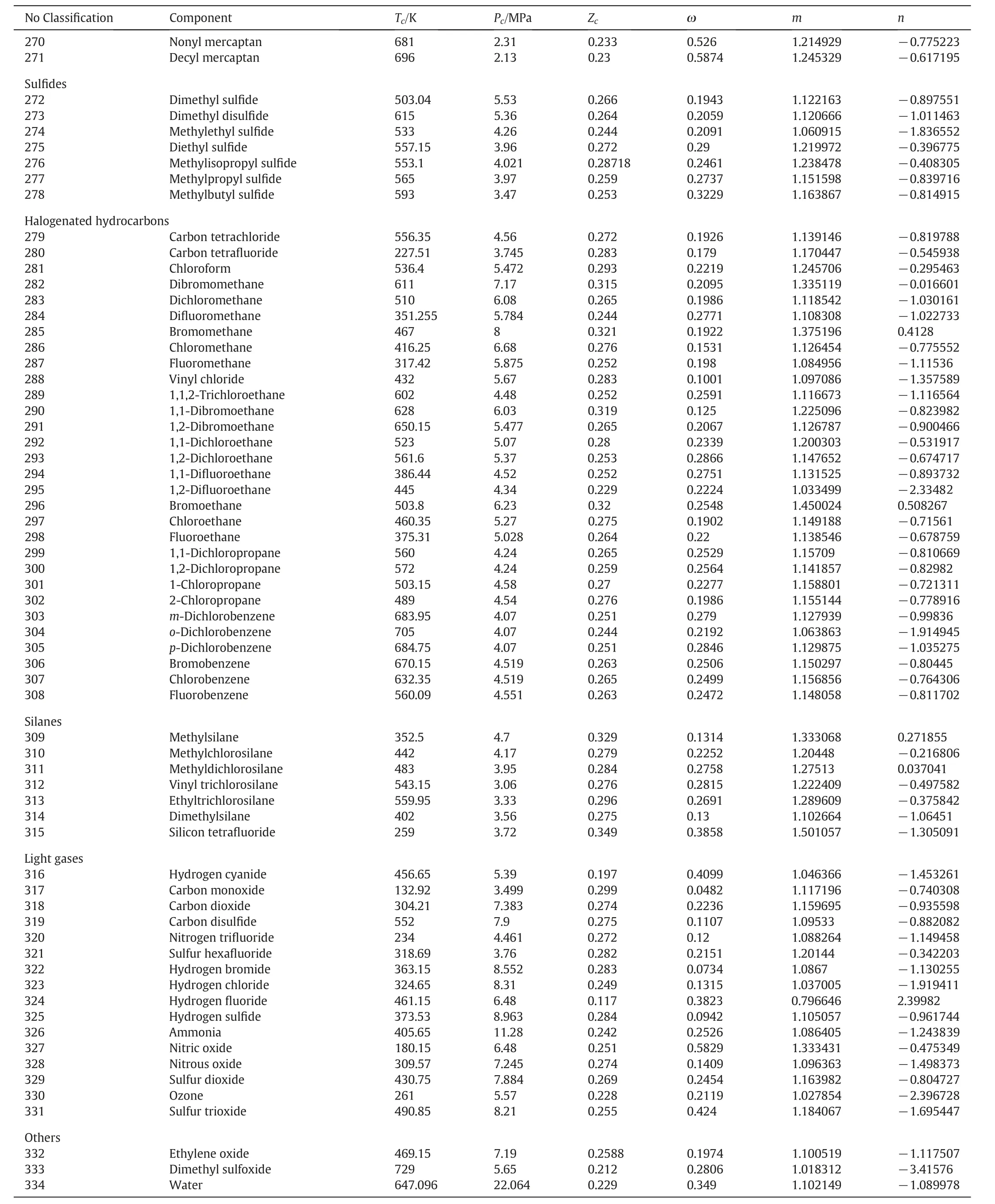
Table 1(continued)

Table 2 AAD of the saturated vapor pressure and liquid density calculated for various equations of state.The experimental data are taken from NIST[41]and Perry's chemical engineers'Handbook[42]

where aijin Eq.(20)is given by the following expression:

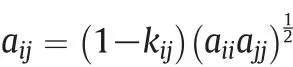
Fig. 3.Experimental and predicted pressure-density plot for various compounds.The experimental data are taken from NIST(National Institute of Standards and Technology)[41].

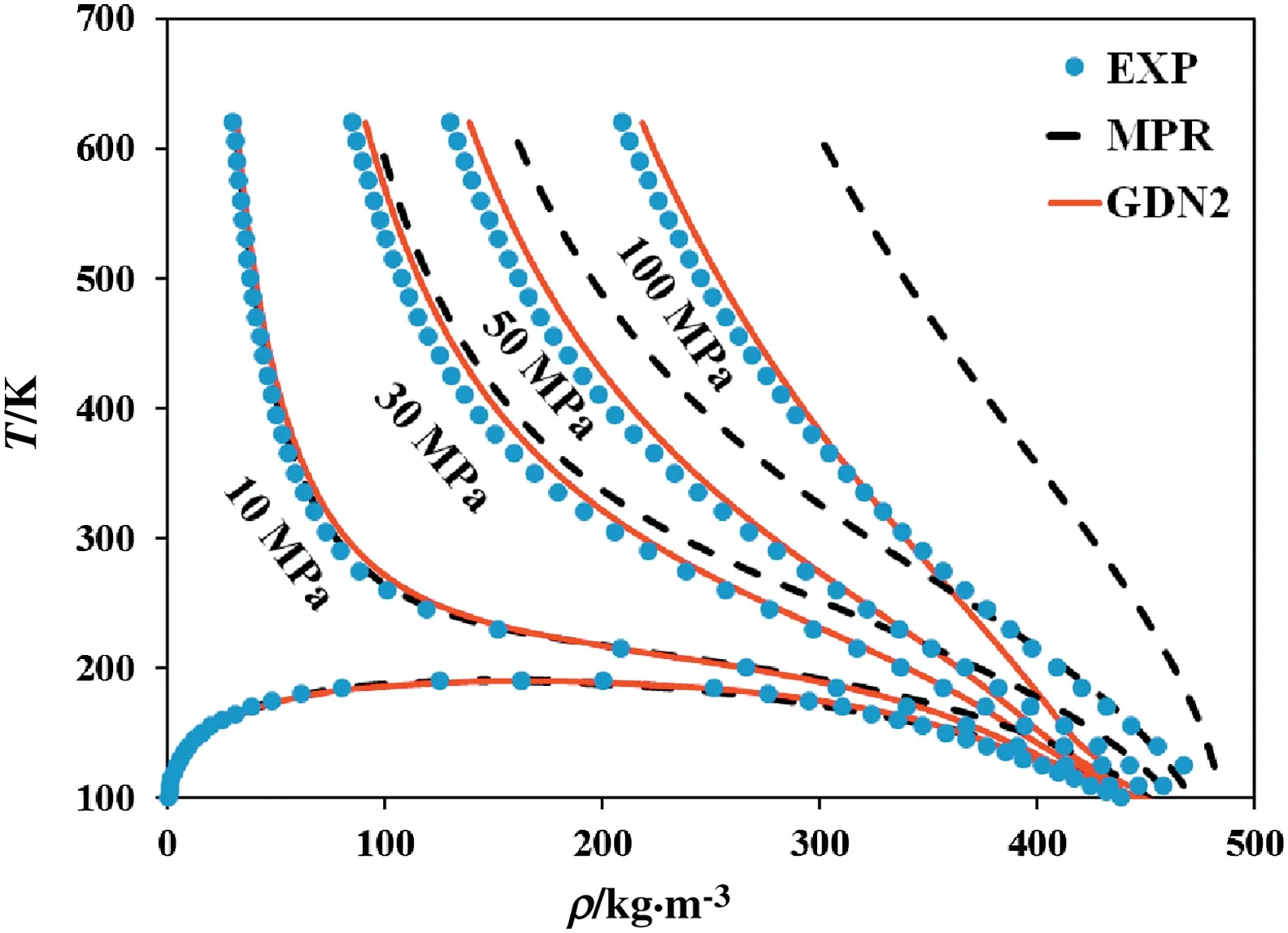
Fig.4.Experimental and predicted PVT plot for methane.The experimental data are taken from NIST[41].

Fig.5.Experimental and predicted PVT plot of ethane.The experimental data are taken from NIST[41].

Fig.6.Experimental and predicted PV plot for carbon dioxide.The experimental data are taken from NIST[41].

Fig.7.Experimental and predicted PV plot for nitrogen.The experimental data are taken from NIST[41].

Here ncis number of pure components and kijis known as the interaction parameter.

Several binary systems were considered for mixture vapor-liquid equilibrium calculations.The interaction parameter kijis obtained by minimizing following objective function.

where,Pbis bubble point pressure,N is number of experimental data points.The interaction parameter for GDN1,MPR,PT and GDN2 equations of state are given in Table 5.

Table 6 represents the results of the bubble pressure and vapor mole fraction using GDN2,GDN1,MPR,and PT EOSs.The MAAD%of the bubble pressure are 2.72%,2.82%,2.89%,and 2.94%and for the vapor mole fractions approximately 3.54%, 3.45%, 2.58%, and 2.33% for GDN2,GDN1,MPR,and PT EOSs respectively.Figs.12 and 13 show phase diagram of the binary system like CH4-C4H10and CO2-C4H10.From the results we,observe that the GDN2 EOS predicts mixture properties at the same level of accuracy as that of the previous EOSs.The predictions forthe mixtures can be improved by using complicated mixing rules.The work is in progress.

Table 3 AAD of the enthalpy of vaporization and compressed liquid density calculated for various equations of state.The experimental data are taken from NIST[41]and Perry's chemical engineers'Handbook[42]

6.Conclusions

A four-parameter GDN2 CEOS is presented to predict properties including saturated vapor pressure and liquid density,compressed liquid density,heat capacity at constant pressure and volume,enthalpy of vaporization,and sound velocity of pure fluids.Using van der Waals onefluid mixing rule,the present CEOS is further used to predict bubble pressures and the vapor mole fractions of binary mixtures.The critical compressibility for each fluid is taken as an experimentally fixed parameter and not as a variable parameter to be used in the fitting.Our formalism results in only one parameter b as a function of temperature,which controls all the other parameters.A noteworthy feature is a significant improvement in the prediction of saturated liquid densities of pure compounds.Further,the GDN2 EOS works satisfactorily for mixtures while being free of the inconsistencies that plagued other CEOS that used a temperature dependent covolume parameter.

Fig.8.Experimental and predicted enthalpy of vaporization for different fluids as a function of reduced temperature.The experimental data of NH3,Ar,and H2O are taken from NIST[41]and of C6H6O and CS2 are taken from Perry's chemical engineers'Handbook[42].

Table 4 AAD of saturated thermodynamic properties of some polar compounds using GDN2 and MPT EOSs

Nomenclature

a Attraction parameter,Pa·m6·mol-2

b Covolume parameter,m3·mol-1

c Semi covolume parameters,m3·mol-1

CpMolar heat capacity at constant pressure,J·mol-1·K-1)

CvMolar heat capacity at constant volume,J·mol-1·K-1

d Semi covolume parameters,m3·mol-1

h Molar enthalpy,kJ·mol-1

N Number of the data points

P Pressure,Pa

R Universal gas constant(8.314462 J·mol-1·K-1)

T Temperature,K

v Molar volume,m3·mol-1

vsSound velocity,m·s-1

x Liquid phase mole fractions

y Vapor phase mole fractions

Fig.9.The isobaric heat capacity of ethane at various constant pressures.The experimental data are taken from NIST[41].

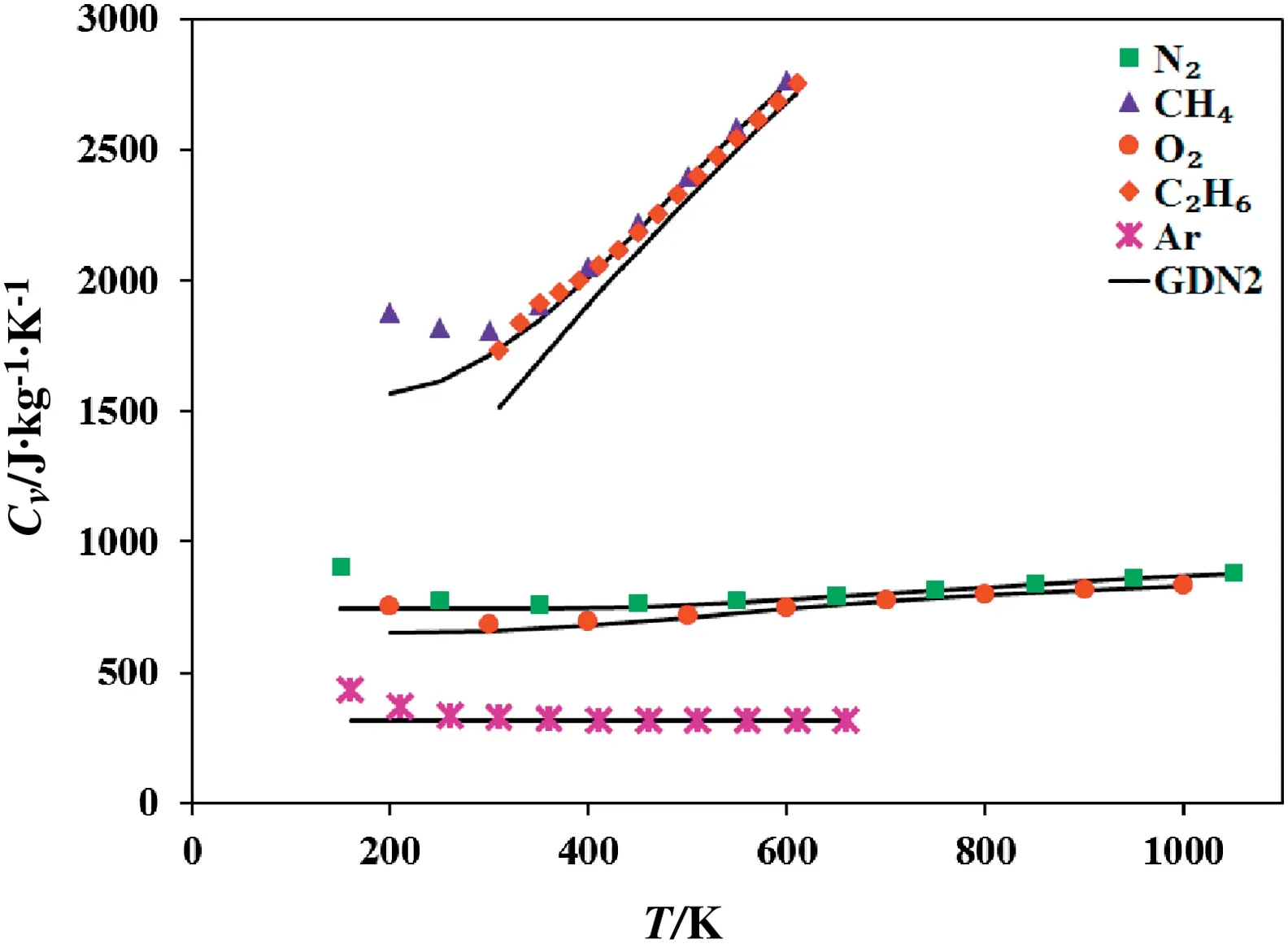
Fig.10.Variation of the isochoric heat capacity of different fluid with the temperature at 10 MPa pressure.The experimental data are taken from NIST[41].

Fig.11.Sound velocity of various fluids at 10 MPa pressure.The experimental data are taken from NIST[41].

Table 5 The interaction parameter kij of binary mixtures using various equations of state

Z Compressibility factor

α Alpha function

ω Pitzer acentric factor

ρ Density

Ω Constants in Eq.(2)

Superscripts

cal Calculated

exp Experimental

Subscripts

bubble Bubble point

c Critical

i,j Dummy index

r Reduced

Acknowledgments

We would like to thank Prof.Ashwin Patwardhan for his suggestions and encouragement throughout the course of this work.This work was supported by the University Grants Commission(UGC-BSR).

Appendix A

1.Fugacity Coeffciient(φ)of Pure Fluid

2.Fugacity Coefficient(φ)of ith Component in a Mixture

where GRis the molar residual Gibbs free energy and is given below:Here a,b,c and d are obtained using mixing rules.

Table 6 AAD of the bubble pressure and vapor mole fraction for different binary mixtures is calculated using various equations of state

Fig. 12. Phase diagram of the CH4-C4H10 binary system calculated at different temperatures.

Fig. 13. Phase diagram of the CO2-C4H10 binary system calculated at different temperatures.

3. Pure Compound Heat Capacity at Constant Pressure and at Constant Volume

4.Sound Velocity

where M is the molecular weight.

5.Enthalpy of Vaporization

where G is gas as phase and L is the liquid phase