张意国，赵长见，赵俊锋，贾生伟

（中国运载火箭技术研究院，北京，100076）

0 引 言

对于大部分运载火箭和弹道导弹而言，助推器工作结束后需要进行分离并被抛掉以降低结构重量。对于一般飞行器而言，在子级助推器分离时刻飞行速度不足以达到第一宇宙速度，使得分离后的助推器在地球引力的作用下将落入地球表面。助推器再入过程由于没有主动控制力的作用，在重力及非线性气动力的作用下将出现复杂的姿态运动。对于助推器再入姿态运动模态（即无控状态下姿态周期性运动规律）[1]进行预示，有助于对助推器回收系统进行设计，同时也有助于发射场安控工作的组织实施。王景国等[2]人采用了传统的基于3DOF模型的落点预测方法对火箭整流罩的残骸落点进行估计，其中通过大量的试验数据进行聚类分析结合工程经验对阻力系数和参考面积这两个关键弹道参数进行了计算。陈彬[3]等人对助推器再入运动的单通道运动特性进行了分析，分析了助推器再入过程姿态运动的稳定性。

为全面准确地描述助推器再入自由运动过程的姿态运动特性，有必要开展其三通道运动模态的研究。对助推器三通道运动模态的研究建立在助推器再入三通道耦合非线性模型的基础上，相较于单通道线性化模型[3]，三通道运动学模型能够提供更高的模型精度，同时也存在不止一组平衡点，对助推器再入动力学特性的描述可以更准确。但也因为非线性模型强耦合以及强非线性的特点，使得基于小扰动理论的线性系统理论对一些系统特性无法展开准确地分析。

本文采用了基于演化搜索算法的改进郭涛算法，解决高阶、强耦合非线性动力学模型的多平衡点求解问题[4～7]，并在此基础上对助推器再入过程平衡点的稳定性及演变规律进行了分析。

1 助推器再入非线性模型

在再入弹头和自旋稳定飞行器动力学的研究中，常使用基于经典欧拉角描述的运动学模型，以便于更好地描述大姿态角运动下的运动规律[8,9]。对于再入助推器而言，其存在大范围的姿态角运动，且姿态角运动存在高动态特性，适合于使用基于经典欧拉角及其角速度描述的姿态动力学模型来进行动力学分析工作。

经典欧拉角的定义如图1所示，包括进动角、章动角及自旋角，是描述助推器体坐标系与准速度坐标系之间转换关系的一组欧拉角，相应坐标系描述如下：

a）助推器体坐标系（Oxbybzb）。

坐标系原点O位于质心，O xb轴沿助推器纵轴向前为正，Oyb在对称平面内指向上为正，Ozb轴与其余两轴满足右手定则。

b）准速度坐标系（Ox5y5z5）。

坐标系原点O位于质心，O x5轴沿速度方向向前为正，O y5位于包含Ox5的竖直平面内向上为正，O z5轴与其余两轴满足右手定则。

由准速度系转到助推器体坐标系为1-3-1转序：首先Ox5y5z5坐标系沿Ox5旋转ζ（进动角）至Ox5y' z'坐标系；然后绕Oz'轴旋转δ（章动角）至Oxby'' z'坐标系；最后绕Oxb轴旋转λ（自转角）至Oxbybzb坐标系。

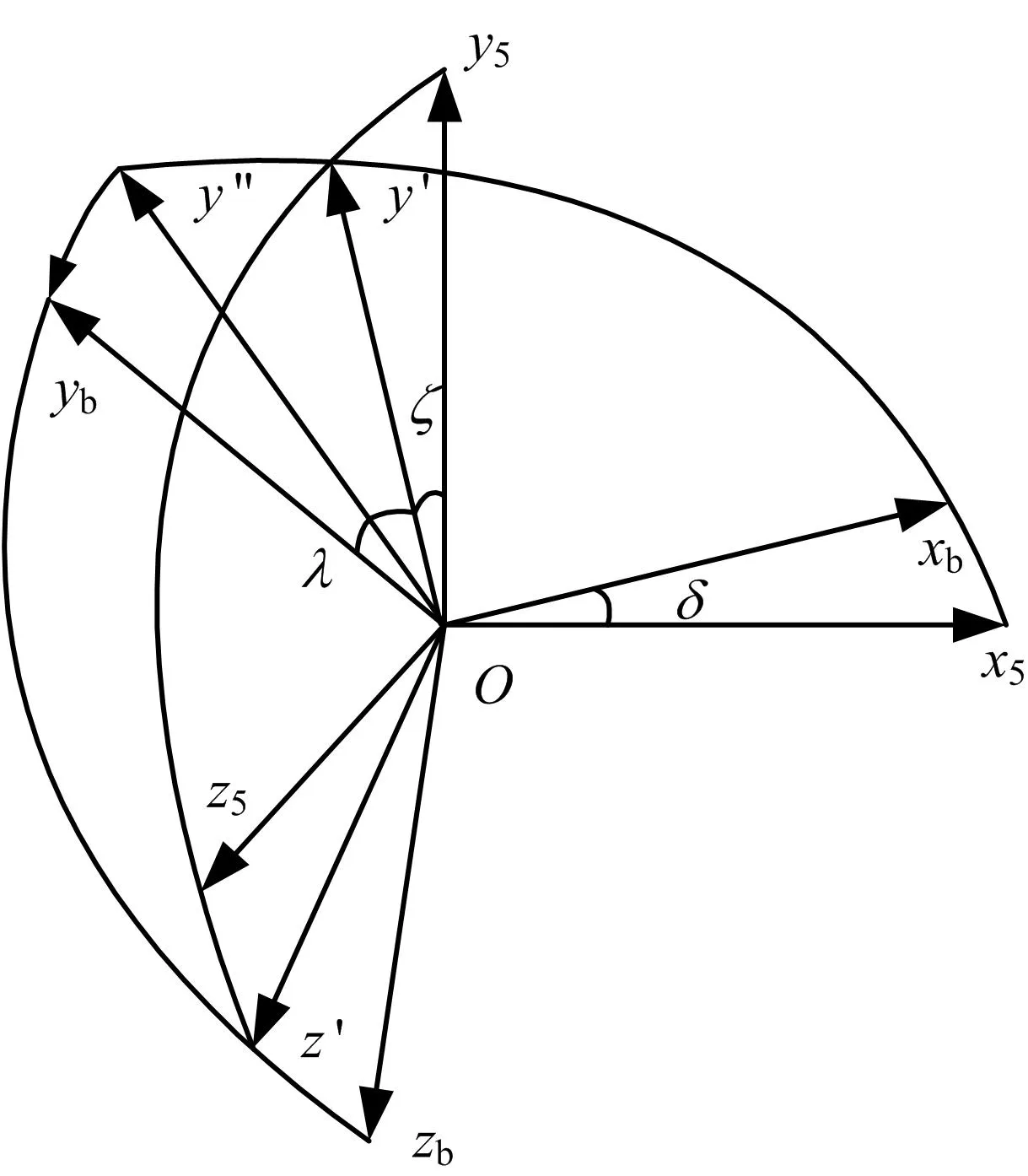
图1 经典欧拉角定义Fig.1 Classical Euler Angle Definitionζ—进动角；δ—章动角；λ—自转角

助推器再入飞行过程没有控制力，只在重力和气动力的作用下自由运动，而空气动力一般在弹体系下描述，是与攻角α及侧滑角β相关的变量，根据坐标转换关系可得到α，β以ζ，δ，λ表示的表达式：

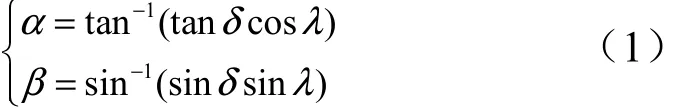
考虑到助推器姿态运动相对质心运动为快时变运动，在分析姿态运动时可以认为助推器速度的大小及方向保持不变，准速度系可视为惯性坐标系，则再入助推器的角速度（xω，yω，zω）可以用δ、ζ及λ的角速度之和表示：

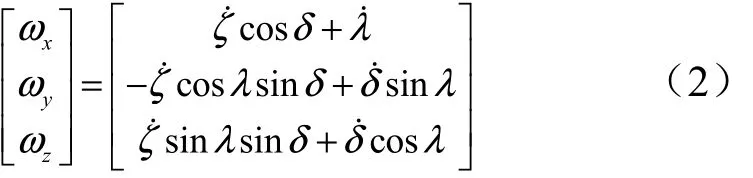
式中xω，yω，zω为弹体系下欧拉角的3个分量；ζ˙为进动角速度；λ˙为自旋角速度；δ˙为进动角速度。

对式（2）进行求导并进行转换，可以得到以欧拉角表示的助推器非线性动力学模型：

式中xω˙，yω˙，zω˙为弹体系下欧拉角速度bω˙的3个分量；δ˙˙为进动角加速度；ζ˙˙为章动角加速度；λ˙˙为自旋角加速度。

可根据欧拉方程求得，矢量形式为

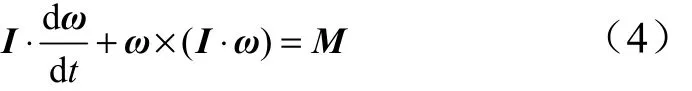
式中 I为弹体转动惯量矢量；ω为弹体角速度矢量；M为合外力矩矢量。

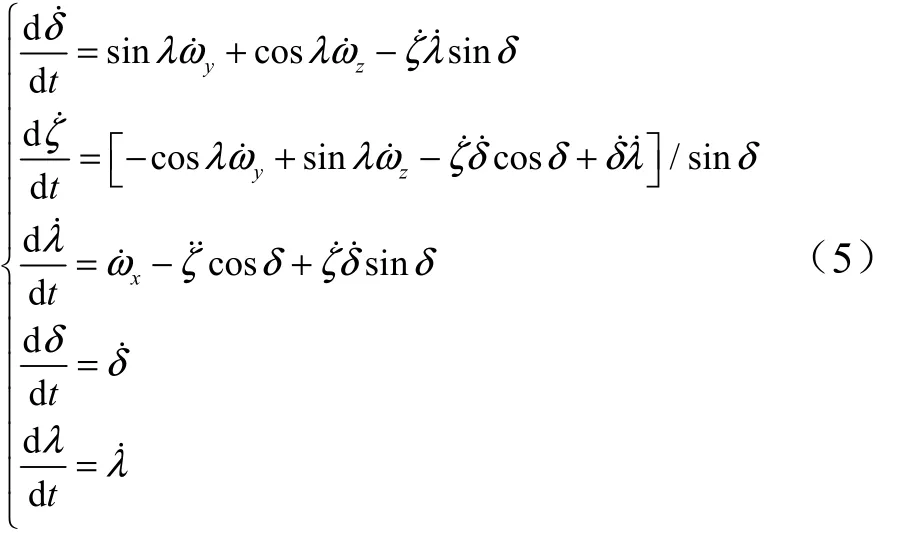
2 非线性模型平衡点求解

对于助推器再入飞行无控姿态动力学系统，为了得到系统在固定参数下的平衡点，需要将模型中的所有状态变量关于时间的导数设为0。以上标“P”表示平衡点处的各状态变量，则得到平衡点处的运动方程：

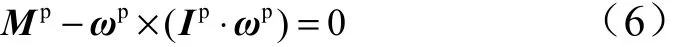
式中 Ip为弹体平衡点转动惯量矢量； ωp为弹体平衡点角速度矢量； Mp为平衡点合外力矩矢量。

式（6）即为平衡状态的运动方程，展开可得到平衡方程的标量形式为

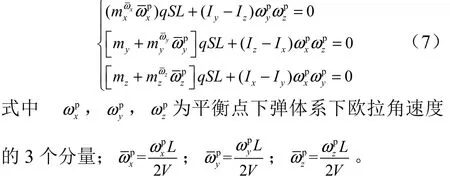
3 郭涛算法

针对高阶强非线性方程组，在理论上不存在解析解，对于该问题的求解一般采用数值方法。比较常用的数值方法包括牛顿法和遗传算法等，但这些算法对初值敏感，求解结果具有局部性，无法实现全局多解的求解，甚至在一些非线性较强的方程组求解过程中会出现直接发散的现象。所以有必要研究对于该类方程组的有效求解方法。

武汉大学的郭涛提出了一种演化搜索算法，其在求解非线性优化问题及多解问题时有独特的优势，能够保证解的全局性，同时收敛速度较快，是一种适合解决本文问题的方法，其特点为：

a）提出了一种基于全局的群体搜索策略，理论上能够保证解的全局性。

b）提出了种群迭代优化策略，采用遗传算法中父代杂交与随机子空间搜索并行策略，保证了在种群优化过程中兼顾搜索的遍历性。

c）提出了末等淘汰策略，种群迭代中每次只淘汰最劣等个体，能够较好地控制种群的整体性。

郭涛算法同时在理论上保证了全局性及遍历性，这样就保证了算法能够依概率一收敛到全局最优解。

该方法的主要求解策略及流程如图2所示。

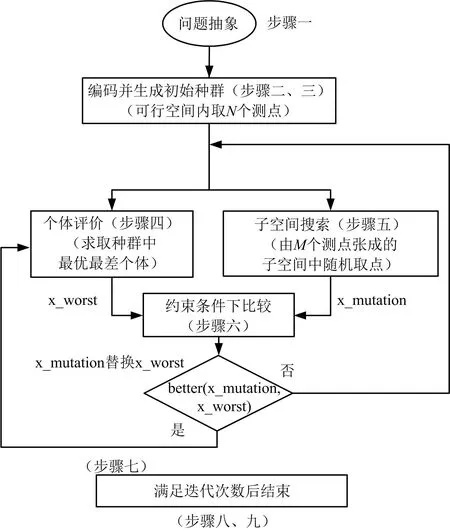
图2 郭涛算法的求解过程Fig.2 Guo Tao Algorithm Solution Process

a）步骤一：问题的描述。

郭涛算法求解的第1步，将常见的非线性多维方程组多解问题抽象为有约束下的最优化问题。

设非线性方程组为

假定该方程组有解，其求解问题可以转化为

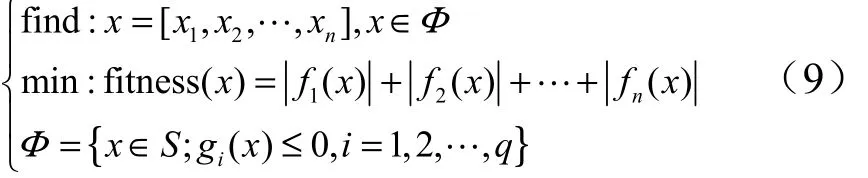
其中，S为搜索空间， S ⊂Rn，当fitness(x):S→R称为目标函数，fitness(x)= 0 时，x为方程组的精确解，通常S是一个n维长方体，即由所确定；Φ为可行点集或可行区域。

b）步骤二：确定编码方式。

确定问题的数学模型后，需要制定研究对象的编码方式，对于复杂的非线性问题，采用浮点数编码能够提高算法求解的准确程度。

c）步骤三：种群初始化。

d）步骤四：个体评价。

本文的优化问题可归纳为连续优化问题，因为约束及解空间在实数空间上是处处连续的，因此针对该问题的求解过程能够保证较好的局域性及精确程度。

用逻辑函数 b etter(x1, x2)表示测试点 x1优于测试点：

定义：

用定义的逻辑运算函数，求解种群中的最优个体xbest和 最 差 值xworst， 使 得 ： ∀x∈P，better(xbest, x) ,better(x, xworst)；如果 b etter(xworst,xbest)，转到步骤八。

e）步骤五：子代优化（父体杂交）。

以相同概率选取上述两种方法中的一种决定搜索空间V，并在V中随机选取一点x。

f）步骤六：劣汰策略。

如果better(x, xworst)，则xworst= x 。

g）步骤七：转到步骤四。

h）步骤八：输出 xbest。

i）步骤九：结束。

4 助推器再入三通道动力学特性分析

4.1 平衡点求解

求解平衡状态非线性方程组时，气动力系数通过攻角α和侧滑角β在（-180°，+180°）范围内插值得到，系统具有定义域范围大和参数强非线性的特点（各特征马赫数下法向力系数NC和俯仰力矩系数MZC的变化规律见图 3、图 4）。传统解非线性方程组的方法如半解析法和牛顿法只能解决小定义域和参数定常的问题，不适用于本文的模型。郭涛算法采用变空间搜索及劣势淘汰策略，对方程组解的搜索具有全局性，不受定义域大小的限制。同时由于郭涛算法基于演化搜索的思想，只要求模型参数可求，不要求其定常或可微，使得郭涛算法具有更强的适应性，适用于本文的参数强非线性模型。

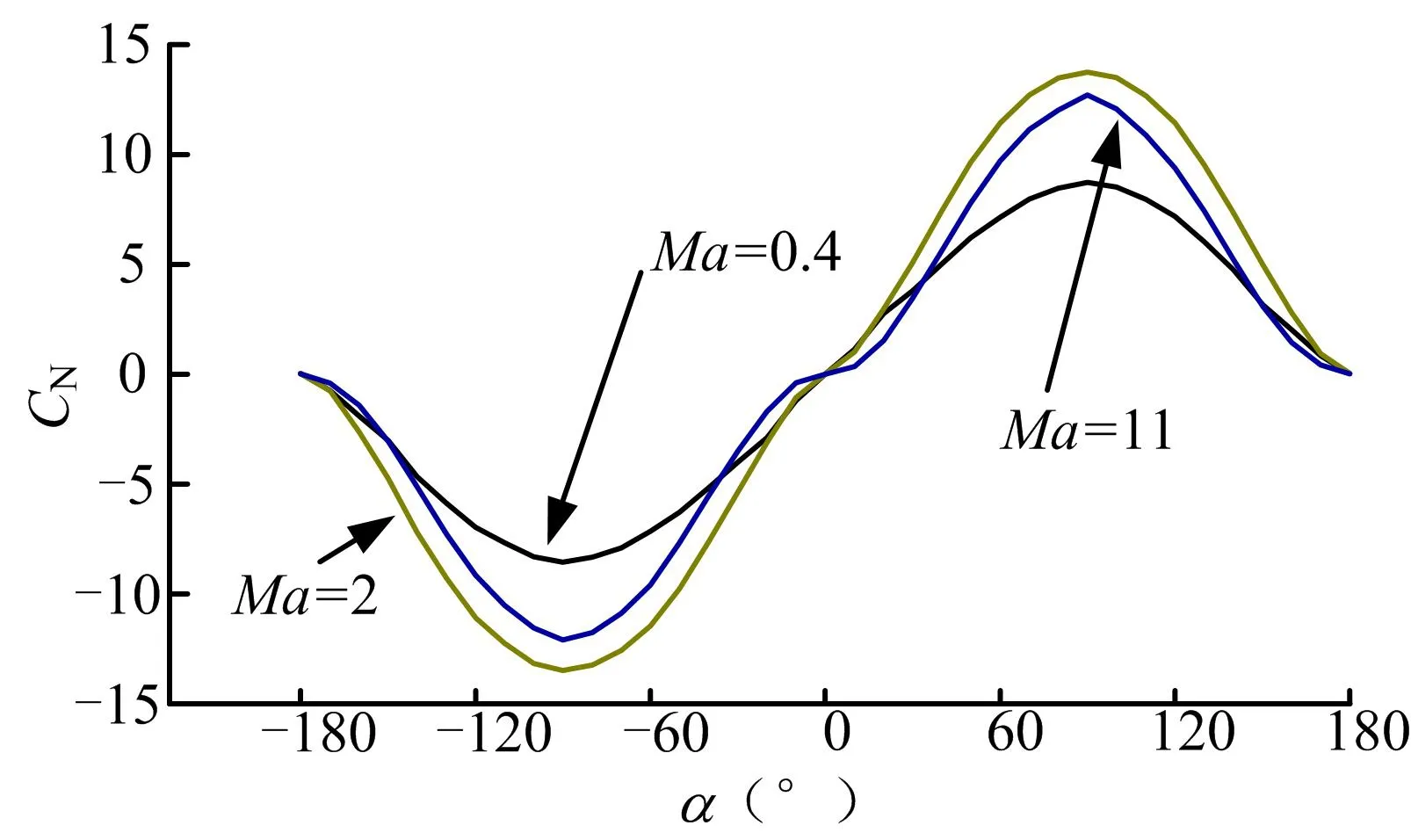
图3 NC 随攻角变化Fig.3 CN’s Relationship to the Change in Angle of Attack

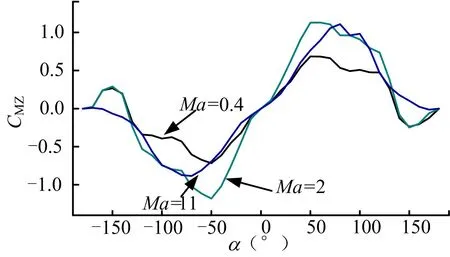
图4 MZC 随攻角变化Fig.4 CMZ’s Relationship to the Change in Angle of Attack

根据非线性微分方程组的特性和助推器气动轴对称的特点，可知若{ζ ˙ ,δ, λ}为方程组的一个解，那么{ζ ˙ ,− δ,π+λ}，{− ζ ˙, δ, −λ}，{−ζ˙,− δ, π −λ}也是方程组的解，且在这 4个解处，系统具有相似的姿态运动规律，可以认为它们代表1个解。因此在下文中仅给出一种解的形式作为相同动态特性解的代表，且如{0 ,π,0} 等显而易见的解也不再记录。最后通过郭涛算法仿真计算得到助推器在不同特征马赫数下对应的非线性姿态运动的平衡点，见表1。

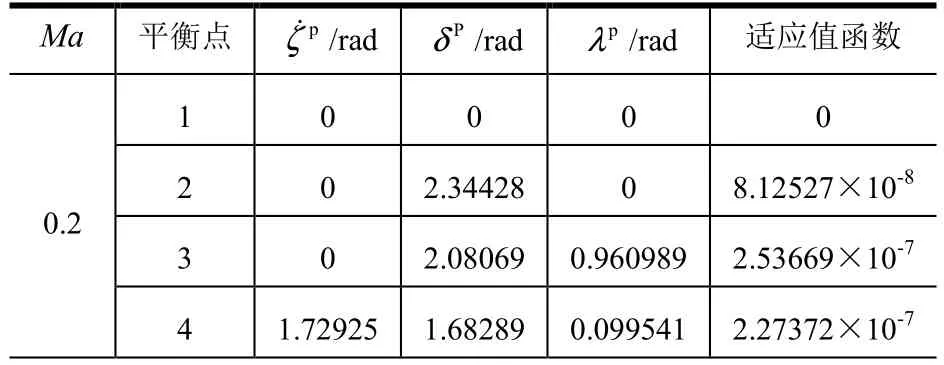
表1 郭涛算法解不同特征Ma下对应非线性模型平衡点Tab.1 Guo Tao Algorithm’s Solutions Depend on Diferrent Ma

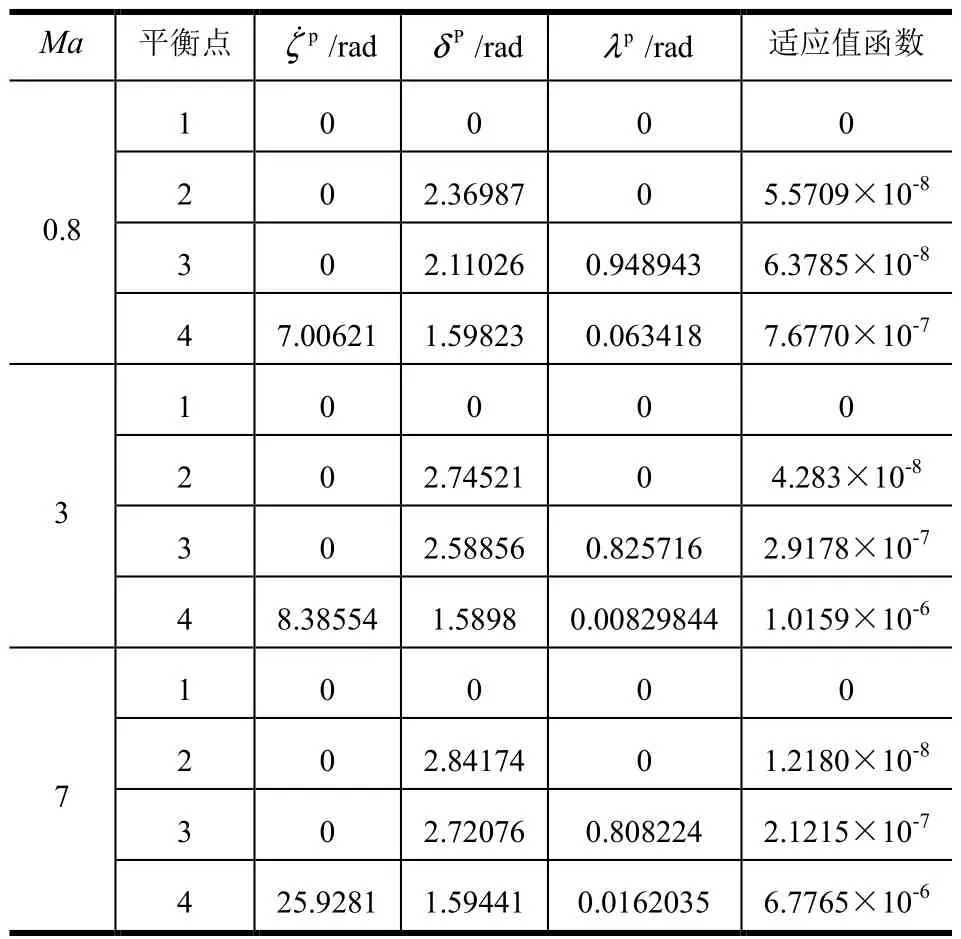
续表1

由表1可知，利用郭涛算法求解出每个特征马赫数下助推器姿态运动非线性方程组存在4组解，每组解对应的适应值函数均接近于零，表明算法精度较高，结果可信。

通过经典欧拉角的定义可知：ζ˙表征助推器的旋转速度；δ表征助推器纵轴与速度轴夹角，等价于总攻角；λ表征助推器纵平面与总攻角平面夹角。通过表 1对不同特征马赫数下的平衡点分析可以得到平衡点随马赫数变化的规律，见图5、图6。由图5以及图6的分析结果知，不同于线性系统，助推器非线性系统存在多组平衡点。不考虑对称分布的相似平衡点，在再入马赫数 M a∈ (1 ,9)的情况下分布着 4组平衡点：其中平衡点1对应δ=0°；平衡点2对应δ≈90°，随着马赫数的增加章动角变化不大，而相应的进动角速度随马赫数增加而增加；平衡点3、4对应δ随马赫数的增加而增加，由δ≈110°向δ≈160°变化。

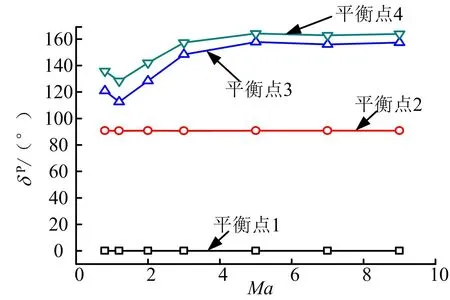
图5 平衡点对应章动角随马赫数变化规律Fig.5 Pδ’s Relationship to the Change in Angle of Attack

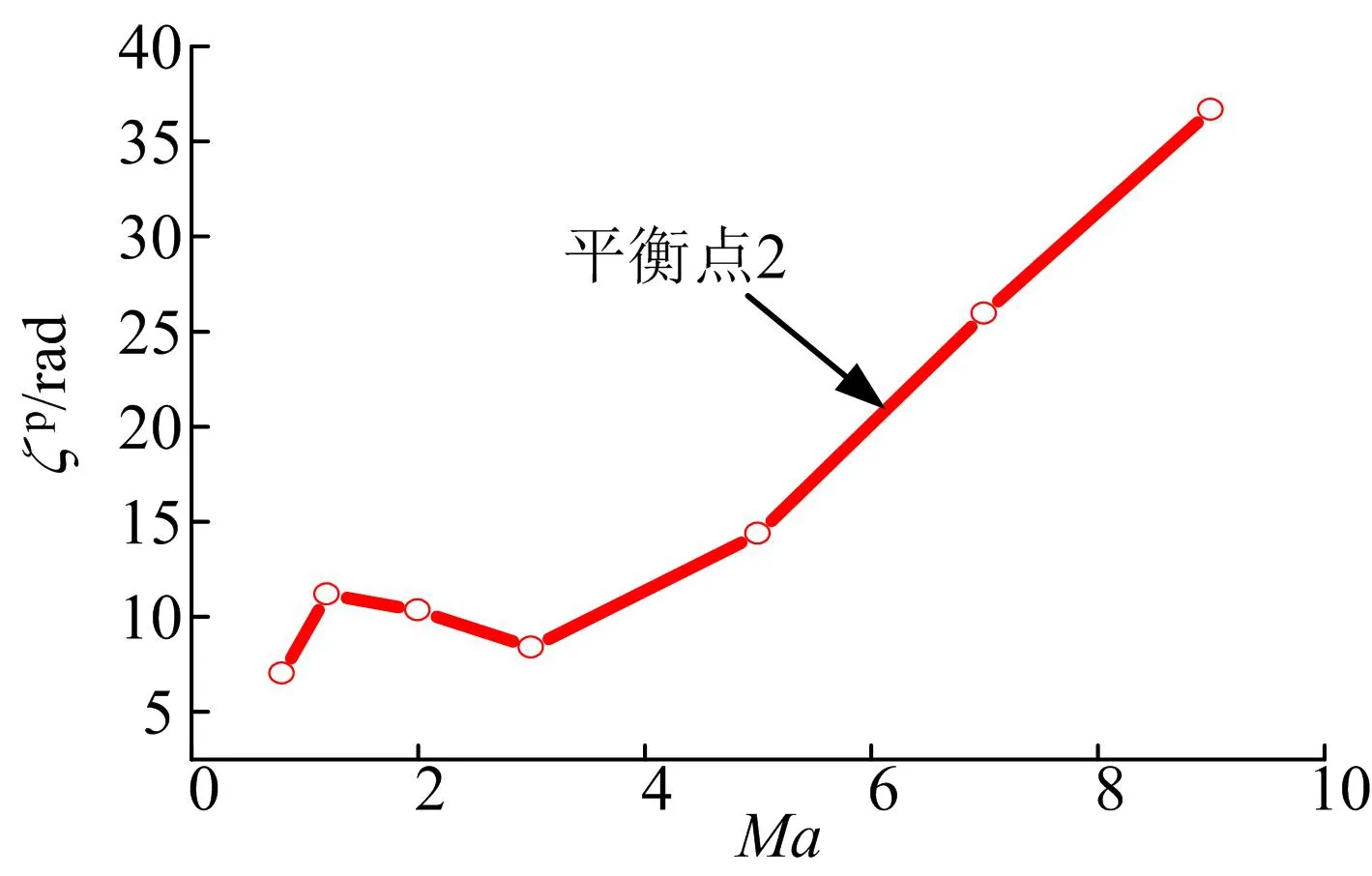
图6 平衡点对应进动角速度随马赫数变化规律Fig.6 ζ ˙p ’s Relationship to the Change in Angle of Attack

4.2 平衡点稳定性分析

助推器再入姿态动力学是强耦合高维非线性系统，很难直接根据李雅普诺夫稳定性的定义来判断其稳定性。对于此类非线性系统，李雅普诺夫第一法（或称间接法）在稳定性的分析中具有着广泛的应用。

李雅普诺夫第一法（间接法）：

若x=0是非线性系统 x˙ =f( x)的一个平衡点，其中f →Rn是连续可微的，设雅克比矩阵为

如果D的所有特征值都满足 R eλi< 0，则原点是渐近稳定的；

如果D至少有一个特征值满足 R eλi> 0，则原点是不稳定的；

如果有某一解的特征根实部在零点而其余特征根的实部为负值，此时则无法判断该平衡点的稳定性。

运用Lyapunov的第1种方法求解本文再入非线性系统平衡点的稳定性，可分析得到平衡点的稳定性随马赫数变化规律，可得到再入助推器姿态动力学平衡点稳定性的变化规律，见图7。

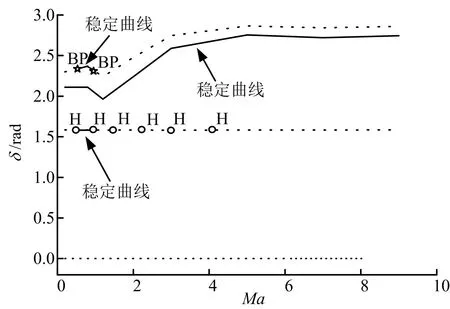
图7 δ解曲线的稳定性Fig.7 Stability of the δ’s Solution

由图7可知，在助推器再入飞行绝大部分马赫数域内，非线性系统具有一组稳定平衡点和3组不稳定平衡点，这意味着在合适的初始条件下系统会被锁定在这一平衡状态下。而在Ma∈（0.76,0.84）这一马赫数域内，系统的2组不稳定解曲线发生了性态变化，演变成稳定平衡解曲线，此时系统存在3组稳定平衡点，意味着在合适的初始条件下系统可能被锁定在其中任意一种平衡状态下。此处以Ma=0.8的工况为例，将不同初始状态对应的相轨迹在δ-δ˙平面上进行投影，所得结果如图8所示。

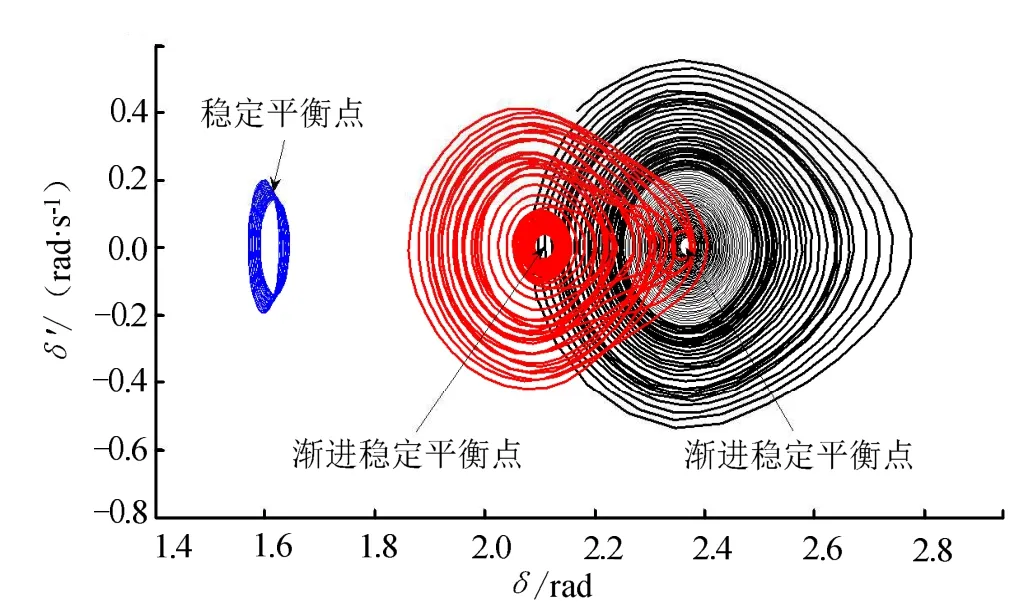
a）相轨迹在δ-δ˙平面上进行投影

续图8

图8 中不同曲线代表的是不同初始条件对应的相图在δ-δ˙平面的投影，从图 8中可以看到在仿真工况下的吸引子包括2个渐进稳定的平衡点和一个稳定的极限环，不同的初始条件会使得助推器的姿态收敛到不同的吸引子，验证了基于演化搜索算法求解的平衡状态的正确性。

将不同初始状态对应的相轨迹在t-ζ˙平面上进行投影，所得结果如图9所示。

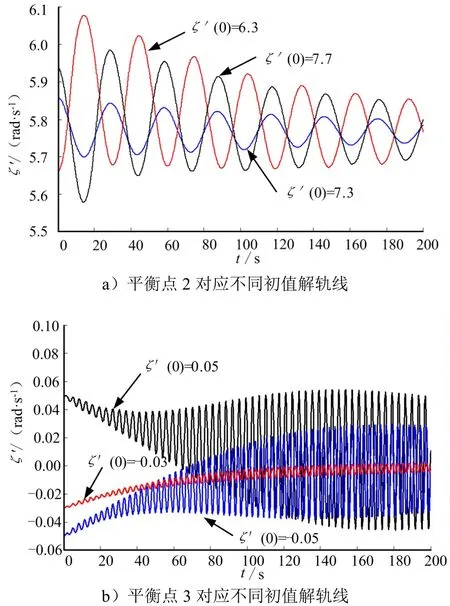
图9 解轨线在t-ζ˙平面投影Fig.9 Solve for the Projection onto t-ζ˙ Plane

由图9可知，在Ma=0.8的工况下，在进动角速度存在初始偏差的情况下，均能收敛到平衡点对应的稳定状态（平衡点2和4）或在平衡点对应稳定状态附近震荡（平衡点3），其中平衡点2对应的稳定进动角速度ζ˙为7.006 21，平衡点3和4对应ζ˙为0。再次验证了平衡点解算的正确性。

5 结 论

本文采用基于演化搜索策略的郭涛算法，解决了助推器再入飞行模态的预示问题。首先推导了以经典欧拉角描述的姿态运动模型，使研究结论更直观，模型更简洁。利用该模型，进一步推导了五维姿态动力学平衡点方程组，并采用基于演化搜索算法的改进郭涛算法解决了非线性方程组的多解问题。进一步，利用Lyapunov第一法对平衡点稳定性进行了分析。最后通过了时域分析的验证。结果表明在再入过程中的特定马赫数域内（Ma=（0.76，0.84））存在3组飞行模态，一组模态对应高速旋转运动，其余两组模态对应姿态稳定运动。进入该飞行速域时的不同初始状态将使助推器姿态运动收敛到不同的飞行模态。

本文提出了助推器无控飞行模态的预示方法，获得了再入飞行速域内助推器可能出现的多个稳定飞行模态，为进一步设计助推器回收系统或精细化设计安控区提供了有力支撑。但本文并未对各模态的稳定域进行分析，如何解决高维非线性模型稳定域的确定将是下一步研究的重点。