宋勃升, 赖乐珊, 李肯立

(湖南大学 信息科学与工程学院, 湖南 长沙 410082)

膜计算是自然计算的分支，它是从生物细胞的结构和功能中抽象出来的计算范式. 自1998年Păun[1]首次提出膜计算概念以来，学者们提出了许多不同的膜计算模型. 一个膜计算系统包含以下几个部分：细胞膜内的物质、进化规则、控制物质转移的蛋白质通道、膜分裂和膜分离等. 最早提出的膜系统属于细胞型膜系统，它的膜结构是分层排列，每个膜包含的区域内含有物质多重集和物质进化规则，每个膜内的进化规则通常以极大并行模式执行计算过程.

膜计算研究主要分为理论研究和应用研究. 理论研究主要关注各类膜系统变型的可计算性、小通用注册机和计算复杂性等. 计算复杂性是近年来膜计算领域一个非常重要的研究方向，已经证明在膜系统中引入膜分裂操作可以在多项式时间内解决NP完全问题，文献[2-4]证明了几类膜系统的计算能力上限为复杂类PSPACE，而文献[5-8]涉及的膜计算模型可以刻画P#P类. 在膜计算应用方面，硅膜启发式算法被用于系统生物学中的建模研究：一方面用于优化和控制方面的研究；另一方面，膜计算模型可以作为人工细胞系统的形式化表达，并且已经有多个侧重于人工细胞系统在合成生物学框架内生物实现方面的研究.

本文主要介绍几类可以有效求解计算困难问题的膜系统，包括介绍活性膜膜系统、膜上带蛋白膜系统、组织膜系统、带膜分裂的同向/反向规则膜系统以及脉冲神经膜系统的相关定义和基本概念[9]；给出了这些膜系统模型的计算效率和计算复杂性；指出了一些可以提高膜系统计算能力的特性；最后给出各类膜系统中存在的一些公开问题.

1 预备知识

多重集M是一个二元组(A,f)，其中f:A→N是一个映射(A是字母表，N是自然数集合).M的支撑集定义为supp(M)={x∈A|f(x)>0}，多重集的基数是指该多重集中重复元素的和. 若多重集的支持集是空集(或有限集合)，则该多重集定义为空(或有限的). 如果M1=(A,f1)，M2=(A,f2)是字母表A上的多重集，那么M1和M2的并集定义为M1+M2=(A,g)，其中g=f1+f2. 用符号P、NP、co-NP和PSPACE表示基本的计算复杂性类型[10]，P#P表示带预判的多项式时间图灵机能够解决的问题类.

定义1一个度为m≥1的膜系统是一个元组

Π=(O,H,μ,w1,…,wm,R,iout),

其中，O是有限字母表；H是膜的标签集合；μ是度为m的膜结构；w1,…,wm∈O*是m个膜中的初始多重集；R是有限的规则集合；iout是输出区域.

Π的格局是当前时刻膜结构μ和存在于所有膜中的物质多重集(初始是w1,…,wm)的元组. 系统的格局通常以最大并行模式(还有其他的规则使用模式，譬如串行和最小并行等)使用规则来转换. 当系统没有可用的规则时，系统停止，输出区域的物质多重集为计算结果.

为了解决判定性问题，通常需要定义识别膜系统.

定义2一个度为m≥1的识别膜系统是一个元组

Π=(O,H,μ,Σ,w1,…,wm,R,iin,iout),

其中,字母表O中包含两个不同的元素yes，no，他们中至少一个包含在初始多重集中，但初始时刻不能出现在环境中；H是膜的标签集合；μ是膜结构；存在一个严格包含在O中的字母表Σ(输入字母表)；wi(1≤i≤m)是OΣ上的初始多重集；iin∈{1,…,m}是输入区域，输出区域iout是环境；所有的计算都停止；如果C是该系统的一个计算，那么，当系统停止时，或者yes或者no(但不是两者)必须出现在环境中.

一个判定性问题X是一个二元组(IX,θX)，其中，IX是一个有限字母表(它的元素称为例子)上的一个语言，θX是IX上的一个全局布尔函数(也就是谓词)[11].

定义3设X=(IX,θX)是一个判定性问题，笔者认为X可以在多项式时间内被识别膜系统族Π={Πu|u∈IX}解决如果以下条件满足：

(1)系统族Π是图灵机在多项式时间内统一的，即关于系统Πu(u∈IX)，存在一个在多项式时间内工作的确定性图灵机；

(2)系统族Π是关于X充分的，如果对每一个例子u∈IX，系统Πu都存在一个接受的计算，那么θX(u)=1；

(3)系统族Π是关于X完备的，如果对每一个例子u∈IX，并且满足θX(u)=1，那么Πu的每一个计算都是一个接受的计算；

(4)系统族Π是多项式有界的，即存在一个多项式函数p(n)，对每一个u∈IX，系统Πu的所有计算都将在p(|u|)步内停止.

因此，系统族Π是判定性问题的一个半统一解.

定义4一个判定性问题X=(IX,θX)在多项式时间内可以被一族识别膜系统Π={Π(n)|n∈N}以统一的模式解决如果满足以下条件：

(1)系统Π是图灵机在多项式时间内统一的，即对于系统Π(n)(n∈N)，存在一个在多项式时间内工作的确定性图灵机；

(2)IX上存在一个多项式时间的计算函数对(cod,s)，使得

①对于任意一个例子u∈IX，s(u)是一个自然数，cod(u)是系统Π(s(u))上的一个输入多重集；

②对每个自然数n∈N，s(-1) (n)是一个有限集合；

③系统族Π是关于(X,cod,s)多项式有界的，即存在一个多项式函数p(n)，对每一个u∈IX，系统Π(s(u)+cod(u))的所有计算都将在p(|u|)步内停止；

④系统族Π是关于(X,cod,s)充分的，即对每一个例子u∈IX，如果系统Π(s(u)+cod(u))存在一个接受的计算，那么θX(u)=1；

⑤系统族Π是关于(X,cod,s)完备的，即对每一个例子u∈IX，并且满足θX(u)=1，那么系统Π(s(u)+cod(u))的每一个计算都是一个接受的计算.

因此,系统族Π是判定性问题的一个统一解.

用PMCC表示由C型膜系统族以统一方式在多项式时间内可解的一类判定性问题. 类似地，用PMCC*表示由C型膜系统族以半统一方式在多项式时间内可解的一类判定性问题.

2 各类膜系统的计算能力

2.1 活性膜膜系统

活性膜膜系统是一类基本的类细胞型膜系统，它的一个重要特征是每个膜上带有三种电荷+，-或0中的一种[1]. 活性膜膜系统含有膜分裂规则，通过使用膜分裂规则，一个膜可以分裂成两个与原膜标签相同的膜，原膜中的物质也将复制到两个子代膜中. 在活性膜膜系统中，学者也研究了将膜分裂替换成膜分离，通过使用膜分离操作，原膜内的物质被分配到子代膜中. 在活性膜膜系统中，还有膜溶解规则，当特定的物质出现在一个膜中时，该膜被溶解，膜内的规则将消失，同时膜内的物质被释放到其父膜中.

定义5活性膜膜系统(简称AM系统)是一个元组

Π=(O,H,μ,w1,…,wm,R,iout)，

其中，O,H,w1,…,wm和iout的概念与定义1中相应元素的概念相同，μ中的膜带指定的电荷+、-或0，R是一个规则集合，具有如下形式：

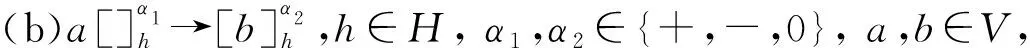
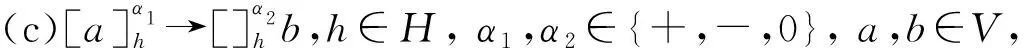
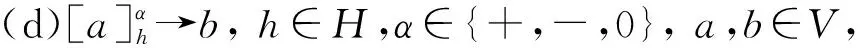
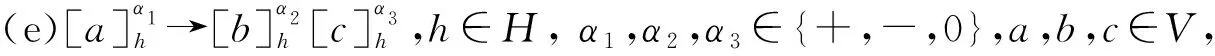
初始格局，系统Π中所有膜的电荷都为0，以最大并行模式运行，直到计算终止. 在一个计算步中，每个物质最多可用于规则类型(a)～(e)的一条规则，每个膜最多可用于规则类型(b)～(f)的一条规则.

表1总结了活性膜膜系统的已知结果[3,5,12-16]，涉及到膜系统(不)允许使用各种类型的规则. 表1中的每一列都定义了允许使用规则类型的特定组合，最后一行显示了仅使用这些类型规则的活性膜膜系统可以解决的问题统一解. 读者可以阅读其详细的证明过程参见文献[17-18].

表1中的结果是膜结构深度不受限制的活性膜膜系统. 当允许非基本膜分裂但膜结构的深度有限时，所得的膜系统可以解决介于P#P和PSPACE之间的复杂类问题[19-20].

表1 识别器带极化的AM系统统一族的计算能力

Table 1 Computational power of uniform families of recognizer AM systems with polarization

规则类型计算能力计算能力计算能力进化规则(a)*XX通讯规则(b)、(c)XXX膜溶解(d)***基本膜分裂(e)X*非基本膜分裂(f)X求解问题类===在多项式时间内PP#PPSPACE

注：X表示允许使用的规则类型；空白表示不允许使用的规则类型；*表示对计算能力没有影响的规则类型.

2.1.1 无极化活性膜膜系统

无极化活性膜膜系统是指该膜系统中所有膜都不具有电荷(用AM0表示无极化活性膜膜系统). 如表2的最后一列所示，当允许使用所有(a)～(f)类型的规则时，AM0系统族仍然能够在多项式时间内解决PSPACE完全问题. 然而，如果AM0不允许使用膜溶解规则，那么该膜系统的计算能力将显著减弱[21].

表2 识别无极化AM系统族的计算能力

Table 2 Computational power of uniform families of recognizer AM systems without polarization

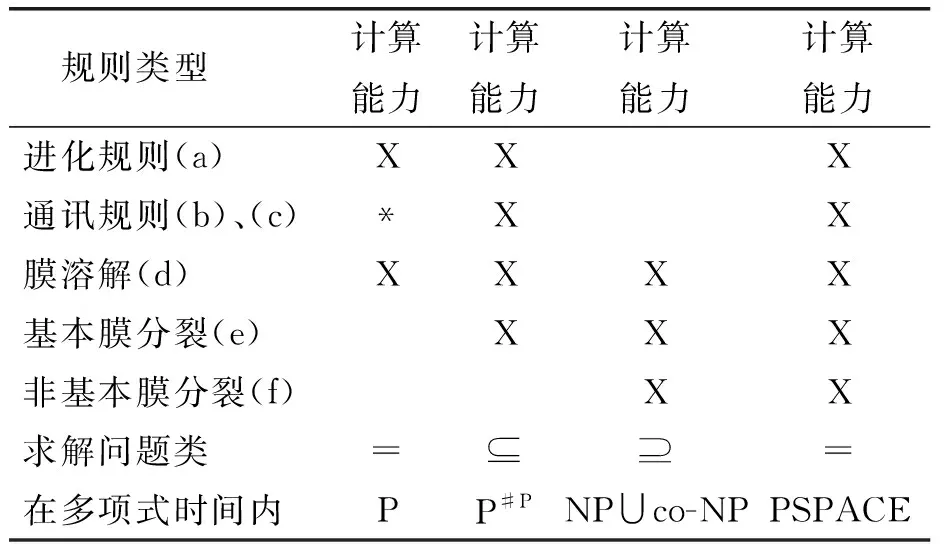
规则类型计算能力计算能力计算能力计算能力进化规则(a)XXX通讯规则(b)、(c)*XX膜溶解(d)XXXX基本膜分裂(e)XXX非基本膜分裂(f)XX求解问题类=⊆⊇=在多项式时间内PP#PNP∪co-NPPSPACE

注：X表示允许使用的规则类型；空白表示不允许使用的规则类型；*表示对计算能力没有影响的规则类型.

如果在只允许使用膜溶解和进化规则的情况下，该膜系统族在多项式时间内的计算能力等价于复杂类P(表2中第一列). 如果系统允许使用类型为(b)和(c)的通讯规则以及限制形式为[a]h→[b]h[b]h(基本膜的对称分裂)的分裂规则(e)，那么系统的计算能力不变. 然而，当系统允许使用基本膜分裂时，系统的计算能力有所提升[5](表2中的第二列). 最后，允许使用规则类型(d)、(e)和(f)的AM0半统一族可以在多项式时间内解决NP∪co-NP[22]中的问题.

表2总结了AM0的一些已知结果[3,15,21-25]. 关于无极化具有活性膜膜系统计算能力的综述可以参考文献[26-27]，该文讨论了进化和通讯规则的各种限制/扩展条件下对系统计算能力的影响.

公开问题1 含有规则类型(a)～(e)的AM0多项式统一族的计算能力是否等价于复杂类P(Păun猜想).

公开问题2AM0系统在使用规则类型(d)、(e)和(f)时的严格上下限.

2.1.2 时间无关的活性膜膜系统

在标准膜系统中，每条规则的执行时间是一个单位时间；而在带时间的活性膜膜系统中，定义了一个时间函数，每条规则的执行时间都由该时间函数确定.文献[28]定义了时间无关膜系统，即对任意的时间函数，系统的计算结果都相同. 文献[29]首次提出了在时间无关模式下求解计算困难问题的概念. 文献[30]第一次给出了活性膜膜系统族在时间无关模式下求解SAT问题. 在时间无关活性膜膜系统中，作者提出了规则启动步的概念，即在某一计算步中，至少有一条规则开始执行时，则该计算步被记为一个规则启动步. 随后其他类型的膜系统(譬如膜上带蛋白质膜系统，组织膜系统)也被证明可以在时间无关模式下的求解计算困难问题，其中包括QSAT问题在内的PSPACE完全问题.

2.1.3 非流利活性膜膜系统

流利活性膜膜系统是指对给定的非确定型膜系统(给定输入)，它可以通过不同的计算途径，最终只能得到一个相同的结果，或者拒绝或者接受. 在这一小节，笔者讨论非流利活性膜膜系统，即相同的膜系统可以同时产生接受和拒绝计算. 在非确定图灵机中，如果至少有一个计算被接受，则认为膜系统接受该输入.

文献[31]证明了即使没有膜分裂，非流利膜系统也能够在多项式时间内解决NP完全问题. 文献[32]证明了深度为1的非流利活性膜膜系统的多项式统一族在使用进化规则、物质送出通讯规则和基本膜分裂规则时，可以在多项式时间内解决PSPACE问题. 由于非流利膜系统在其计算过程中最多可以使用的计算空间为指数个，因此文献[33]给出了EXPSPACE计算能力的上界.

公开问题3非流利活性膜膜系统统一族是否能够刻画复杂类PSPACE.

2.2 带膜分裂的同向/反向规则膜系统

带膜分裂的同向/反向规则膜系统实际上是将同向/反向规则和膜分裂引入到膜系统中[34]. 同向/反向是指物质在细胞或环境内进行位置的移动或交换，物质本身不发生变化. 在同向/反向规则中，每条规则可以有任意多个物质参与.

同向规则的形式是(u,in)或(u,out)，多重集物质u被送进膜内或被送出膜.

反向规则的形式是(u,out;v,in)，多重集物质u被送出膜的同时，多重集物质v被送入该膜中.

文献[34]证明了仅使用同向/反向规则膜系统具有计算通用性，学者们又提出了该模型的许多变型. 文献[35]中提出了带膜分裂的同向/反向规则膜计算模型，在使用基本膜分裂规则和通讯规则长度不超过时，证明了该膜系统可以在线性时间内求解NP完全问题(子集和问题)的统一解. 当同向/反向规则膜系统中允许使用非基本膜分裂时，该膜系统可以在多项式时间内求解PSPACE完全问题(QSAT问题)的统一解. 笔者推测PSPACE问题也是带非基本膜分裂的同向/反向规则膜系统在多项式时间内计算能力的上限.

2.3 膜上带蛋白的膜系统

受膜上膜蛋白控制物质进出细胞这一生物事实的启发，Păun等[36-38]提出了膜上带蛋白的膜系统模型.

定义6带膜分裂的膜上带蛋白膜系统是一个元组

Π=(O,P,μ,w1/z1,…,wm/zm,E,R1,…,Rm,io),

其中：O是物质的集合，P是蛋白质集合，O∩P=∅；

μ是膜结构(一颗根树)；

w1,…,wm是m个膜中的物质多重集；

z1,…,zm是m个膜上的蛋白质多重集；

E⊆O是环境中的物质多重集；

R1,…,Rm是m个膜中有限规则集；

io是输出区域.

在带膜分裂的膜上带蛋白膜系统中，当使用某条规则时，该规则中物质的位置可以发生改变，该物质也可能发生进化，同时与该规则涉及的膜上的蛋白质也可能发生改变.膜上带蛋白膜系统有以下几种规则的类型(表3)，其中a、b、c和d是物质，p和p′是蛋白质，i是膜的标签.

表3 膜上带蛋白膜系统的规则类型

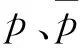
使用以下形式表示膜分裂(称为类型6)，其中p、p′、p″是蛋白质(可能相等)：

[p|]i→[p′| ]i[p″| ]i.

膜i可以是非基本膜. 分裂产生的膜与原膜标签相同，原膜内的物质和膜上的蛋白质(除了p′和p″之外)也将复制到新产生的两个膜中. 文献[4]证明了带膜分裂的膜上带蛋白膜系统可以在多项式时间内求解QSAT问题，该文进一步证明了复杂类PSPACE是该类膜系统计算能力的上界. 文献[41]证明了带膜分裂的膜上带蛋白膜系统可以在多项式规则启动步内以时间无关的模式求解QSAT问题.

公开问题4带膜分裂的膜上带蛋白膜系统能否在只允许使用“res”类型规则情况下求解QSAT.

公开问题5膜上带蛋白膜系统在什么限制条件下可以刻画计算复杂类P.

2.4 组织膜系统

组织膜系统的基本思想是将细胞型膜系统的树状结构推广到任意图结构[42-43]. 因此，组织膜系统中任何两个细胞可以直接进行通讯. 通常组织膜系统中的规则为同向/反向规则，近年来，学者们提出了许多组织膜系统的变型[44-48]，并证明了绝大多数组织膜系统的变型具有图灵通用性.

定义7一个度为m≥1的组织膜系统是一个元组

Π=(Γ,E,M1,…,Mm,R,iout),

其中：

Γ是物质的有限字母表；

E⊆Γ是初始时刻位于环境中的物质集合；

Mi(1≤i≤m)是初始时刻m个细胞中的有限物质多重集；

R是形式为(i,u/v,j)的有限通讯规则集，i,j∈{0,1,2,…,m}，i≠j，u,v∈Γ*，其中规则的长度定义为|uv|>0；

iout∈{0,1,2,…,m}是输出区域.

当使用规则(i,u/v,j)时，物质多重集u从细胞i送到细胞j，同时物质多重集v从细胞j送到i. 如果u=λ或v=λ，则该规则称为同向规则.

用TC表示识别组织膜系统. 根据文献[49]，得出如下结果：

P=PMCTC.

2.4.1 带细胞分裂的组织膜系统

受活性膜膜系统中膜分裂规则的启发，Păun将膜分裂引入到组织膜系统中.

分裂规则:[a]i→[b]i[c]i，i∈{1,2,…,m},a,b,c∈Γ,i≠iout.

如果细胞i中存在物质a，则细胞i分裂成两个具有相同标签的细胞，在两个子细胞中，原始物质a分别进化为物质b和物质c，原细胞中的其他物质被复制到两个子细胞中. 当细胞在分裂时，该细胞不能与其他细胞发生通讯.

笔者用TDC(k)表示带细胞分裂且通讯规则长度最长为k的组织膜系统. 当通讯规则的长度不受限制时，直接省略k. 显然，当k≥j≥1，TDC(j)⊆TDC(k)⊆TDC.

如果通讯规则的最大长度k=1，则带细胞分裂识别组织膜系统刻画复杂类P[50]：

P=PMCTDC(1).

如果通讯规则的最大长度k=2，则带细胞分裂识别组织膜系统可以求解NP完全问题[51]:

NP∪Co-NP⊆PMCTDC(2).

如果通讯规则的长度k≥4，可以得到如下结论[6]:

PMCTDC(4)=PMCTDC=P#P.

近年来，学者们对带细胞分裂的组织膜系统在时间无关模式下求解NP完全问题进行了深入研究，譬如文献[52-53]用带细胞分裂的组织膜系统在时间无关模式下求解了最大团问题、汉密尔顿路径问题和子集和问题. 然而，带细胞分裂的组织膜系统是否能在时间无关的情况下求解P#P中的问题仍然是个公开问题.

2.4.2 具有细胞分离的组织膜系统

膜分离作为另一种可以增加膜数量的操作在文献[54]中被首次提出. 与膜分裂不同，当执行膜分离操作时，原细胞中的物质被分配到两个子代膜中. 笔者把字母表Γ分成两个非空集合，即Γ=Γ1∪Γ2，Γ1,Γ2≠∅，Γ1∩Γ2=∅.

分离规则：[a]i→[Γ1]i[Γ2]i，其中i∈{1,2,…,m}，a∈Γ,i≠iout.

细胞分离规则[a]i→[Γ1]i[Γ2]i能够被使用当且仅当细胞i中存在物质a.当该条规则被使用时，细胞i被分裂成两个具有相同标签的细胞，物质a被消耗，细胞i中存在的其他物质被分配到两个子细胞中，这样，来自集合Γ1的物质被分配在第一个细胞中，来自集合Γ2的物质被分配在第二个细胞中.

笔者用TSC(k)表示带细胞分离和通讯规则的长度至多为k的识别组织膜系统，用TSC表示带细胞分离和讯规则长度不受限制的识别组织膜系统.

当通讯规则的长度k=2时，带细胞分离的组织膜系统刻画复杂类P[55]:

P=PMCTSC(2).

当通讯规则的长度k≥3时，带细胞分离的组织膜系统可以求解NP完全问题[55]：

NP∪Co-NP⊆PMCTSC(3).

文献[6]给出了在对通讯规则长度不受限制情况下的结论:

PMCTSC=P#P.

文献[6]中的结果改进了文献[2,56]中给出的组织膜系统计算能力的上限PSPACE. 更多有关带细胞分裂/细胞分离组织膜系统的计算复杂性和计算效率问题可参见文献[57-58].

公开问题6研究带细胞分裂或细胞分离的组织膜系统在只允许使用同向(或只允许使用反向)规则情况下的计算能力.

2.5 脉冲神经膜系统

脉冲神经膜系统(简称SN P系统)是受生物神经系统中电脉冲信息传递启发[59]的一类膜系统. 与组织膜系统类似，SN P系统的结构用拓扑有向图描述，有向图的节点对应于神经元，弧对应于突触. 一个神经元同时向所有与其有向弧相连的神经元传递脉冲. 脉冲在神经元中积累(就像活神经细胞中的电位)，脉冲数触发控制神经元脉冲的激发规则.

SN P系统从神经元中初始给定的脉冲开始计算，以极大并行模式使用激发规则. 计算结果可以定义为两个脉冲之间的间隔长度或者指定神经元中累积的脉冲数量.

定义8一个度为m≥1的脉冲神经膜系统是一个元组

Π=(O,σ1,…,σm,syn,in,out),

其中：

O={a}是字母表(a为脉冲).

σ1,…,σm是神经元，具体形式为σi=(ni,Ri)，1≤i≤m，

其中：

ni≥0是σi中包含的初始脉冲数.

Ri是具有以下两种形式的有限规则集：

E/ac→a;d，其中，E是正则表达式，c≥1和d≥0；

as→λ，s≥1，对来自Ri每条类型(1)的规则E/ac→a;d，都满足as∉(∈)L(E)；

syn⊆{1,2,…,m}×{1,2,…,m}，对任意的1≤i≤m，均有(i,i)∉syn；

in,out∈{1,2,…,m}分别表示输入和输出神经元.

激发规则E/ac→a;d可以使用当且仅当神经元σi包含k个脉冲，并且ak∈L(E)，k≥c. 当使用该激发规则时，包含该规则的神经元消耗c个脉冲，并且它在d个单位时间后产生一个脉冲，在这d个单位时间内，该神经元处于关闭状态，不接收新的脉冲.

规则as→λ称为遗忘规则，遗忘规则可以使用当且仅当神经元σi正好包含s个脉冲，当使用遗忘规则时，σi中消耗s个脉冲. 在每个单位时间中，如果神经元σi可以使用Ri中的规则，那么必须以非确定性的方式随机使用其中的一条规则.

为了研究SN P系统的计算效率，学者们引入了能够在多项式时间内产生指数数量神经元的操作(如神经元分裂、神经元芽殖等)，证明了该膜系统可以在多项式时间内求解NP完全问题[60-63].

公开问题7能否给出带神经元分裂或芽殖的SN P系统的精确刻画复杂类.

公开问题8有预先计算资源的SN P系统能否精确刻画复杂类PSPACE.

3 结 论

本文介绍了几类常用的膜系统以及其各种变型，分析了各类膜系统(活性膜膜系统、膜上带蛋白膜系统、组织膜系统、带膜分裂的同向/反向规则膜系统以及脉冲神经膜系统)的计算能力，并给出了一些相关模型中存在的公开问题.

目前膜计算中研究的计算效率和计算复杂性问题都是考虑在各类膜系统中引入膜分裂、膜分离、膜产生等能使膜数量增加的操作，利用空间换时间的方式，在指数个膜内同步进行计算. 一个公开问题是如何在不使膜数量增加的情况下，研究膜系统的计算复杂性.

环境对各类膜系统的计算能力起着重要作用，因为笔者通常假设环境中的每种物质都是任意多的. 一个公开问题是研究各类膜系统在环境中物质为空集或者环境中每种物质的数量为有限时的计算能力.