变分方法与交叉科学
2019-07-01丁彦恒
丁彦恒
(1.中国科学院 数学与系统科学研究院, 北京 100190; 2.中国科学院大学 数学科学院, 北京 100049)
0 引 言
变分原理是自然界事物遵从的客观法则.世界是由物质构成的,万物处于永不停息的运动中.运动是物质的根本属性和存在方式.运动自然的和力及能量紧密联系.运动能量泛函的变分对应着事物的拉格朗日方程,即所谓的数学模型,它描述事物的状态,诸如存在性、演化性,等等.因此,变分理论是研究事物的重要方法.
变分学历史悠久,它的起源可追溯到16世纪最速曲线问题. 史上许多大数学家都在这一领域做出了非常大的贡献,如伯努力、欧拉、柯西、拉格朗日、牛顿和莱布尼茨、庞加莱、希尔伯特,等等.
变分方法是含着金钥匙出生的,它激励着数学的发展——助力经典理论、孕育新的学科.特别如:实分析 (Lebegue 测度与积分)、 泛函分析 (强、弱拓扑,单调算子,Sobolev 空间)、偏微分方程 (椭圆型方程,存在性和正则性)、 几何变分 (测地线, 极小曲面,调和映射,Finsler 几何: Garding, Vishik, Agmon, Douglise, Nirenberg, De Giorgi)、几何测度 (极小子流形: J. Nash)、 变分不等式 (自由边值问题: J. Moser, Stampacchia, Lions, Ladyzenskaya Uraltseva)、优化控制 (R. Bellman, L.S. Portryagin, J. L. Lions)、 大范围变分 (临界点理论、Morse 理论、Floer 同调、辛容量)、有限元方法,等等.
变分学的发展对科学特别是自然科学发挥着日益重要的作用.譬如,物理学中的变分问题:Newton 方程、Hamilton 系统、Maxwell 方程 (电磁场)、Einstein 方程 (重力场)、Yang Mills 方程 (规范场);几何学中的变分问题:测地线、极小曲面、调和映射;其它学科如:Dirichlet 原理、电流分布、Riemann 映射定理、Weierstrass 反例、Schwarz 方法、 Neumann 方法、Poincare 方法.Hilbert 在 ICM1900 宣布的23个著名数学问题中有3个涉及变分方法,即第19(正则性)、第20(存在性)、第23(发展变分理论).
就变分学直面的泛函而言,一般分为两类:
•(下方)有界泛函的变分方法 典型例:
-直接方法 经典的变分理论表现在研究泛函的极值问题. 相当长时期内常用直接变分方法, 其中一个代表性定理如是说.
设X是一个可分 Banach 空间的共轭空间 (例如,自反Banach 空间). 又设E⊂X是一个弱*序列闭非空子集. 若f:E→弱*序列下半连续且强制的 (即,∀x∈E, 当时,f(x)→+∞), 则f在E上有极小值.
-Ekeland 变分原理 设(X,d)是一完备的度量空间,f:X→∪{+∞},f≢+∞,下方有界,且下半连续.若 ∃ε>0,xε∈X使得则 ∃yε∈X满足
(1)f(yε)≤f(xε);
(2)d(yε,xε)≤1;
(3)f(x)>f(yε)-εd(yε,x)∀x∈X{yε}.
• 无界泛函的变分方法 典型例:
- 近代变分法—临界点理论 (参阅文献[1-26]), 始于: 1973 年; 着力点: 上下方均无界的泛函的临界点(非极值问题); 重要内容包括:
∘ 极大极小方法;
∘ 指标理论;
∘ (无穷维) Morse 理论;
∘ 标志性工作:(山路定理 1973; Hamilton 系统周期解 1978; 对偶变分法 1978; 集中紧性原理 1984; 对称摄动方法1984等); Floer 同调 1988;
∘ 强不定问题的变分方法.
1 变分框架
这里介绍的变分框架,是笔者及其合作者针对强不定问题建立的,但它对半定问题自然也是适用的.其原创点: 利用自共轭算子的绝对值构造工作空间; 利用线性算子插值理论研究空间的嵌入性质, 利用算子的谱进行空间分解,进而给出非线性条件,得到泛函的规范结构以适合应用临界点理论[2,5,26]
考虑形如
Au=N(u),u∈H
(1)
的半线性方程,这里,H代表Hilbert空间,A是(无界)自共轭算子,其定义域(A)⊂H,N:(A)→H是(非线性)梯度映射,换言之,存在函数ψ:(A)⊂H→H使得N(u)=ψ(u). 形式上,式(1)的解是泛函
(2)
的临界点,其中(·,·)H记H的内积 (其对应的范数记作‖·‖H).一般而言,式(2)没有提供足够的信息.注意Φ仅定义于H的一个真子空间上,应用中很难对ψ给出可验证的条件以保证式(1)的解的存在.例如,如何处理量子力学中的非线性Dirac 系统、力学中的无穷维 Hamilton系统、反应-扩散系统呢?需要选择合适的工作空间E(既不能“太大”也不能“太小”),在E上重新恰当地表示Φ使得它的临界点对应问题(1)的解、且具有易于研究的表达形式. 这就是建立变分框架(或变分原理).
以σ(A)、σe(A)及σd(A)分别记A的谱、本质谱及有限重特征值集合.根据算子理论,Hilbert空间H具有正交分解:
H=H-⨁H0⨁H+,u=u-+u0+u+.
使得A在H-和H+分别是负定和正定的,H0是A的零空间.以{E(λ):λ∈}记A的谱族,U=I-E(0)-E(-0),|A|记A的绝对值,|A|1/2记|A|的平方根.由定义,U与A、从而与|A|1/2可交换.取E=(|A|1/2), 并在E上引进内积
(u,v)E=(|A|1/2u, |A|1/2v)H+(u,v)H.
以‖·‖E记(·,·)E导出的范数.则E有关于内积(·,·)H和(·,·)E都正交的分解:
E=E-⨁E0⨁E+,u=u-+u0+u+
(3)
其中,E±=E∩H±与E0=H0.
设ψ∈C1(E,)且ψ′(u)=N(u) (在应用中,只要对非线性项作适当的假设,就能满足这一要求).在E上定义泛函
-ψ(u), ∀u=u-+u0+u+∈E
(4)
则Φ∈C1(E,).进一步,当u∈(A)是Φ的临界点时,它就是方程(1)的解. 事实上,对任何v∈E,
0=(|A|1/2u+, |A|1/2v+)H-
(|A|1/2u-,|A|1/2v-)H-(N(u),v)H=
(|A|(u+-u-),v)H-(N(u),v)H=
(|A|Uu,v)H-(N(u),v)H=
(Au-N(u),v)H.
注1式(3)直接来自σ(A)的分解.
(1)当0至多是A的有限重特征值时,为更方便起见,通常在E上定义下述等价内积
(u,v)=(|A|1/2u,|A|1/2v)H+(u0,v0)H.
此时,以‖·‖记由 (·,·)导出的范数,Φ可表示为
(5)
(2)记σ-=σ(A)∩(-∞,0)和σ+=(0,∞), 当σ-由至多有限多个有限重特征值组成时,称方程(1)为半定的;当σ-由无穷多个有限重特征值组成时,称方程(1)为不定的. 此外称方程(1)是强不定的,如果σ±各是无穷集;称方程(1)是非常强不定(或本质强不定)的, 如果σ±各含有本质谱.
(3)注意: 由强不定性有dimE±=∞; 应用中要紧的是E的某种嵌入性质 (关联到应用中非线性ψ的合适性).
现代临界点理论初期,大都处理半定或强不定问题,20世纪90年代以来,人们越来越对强不定问题感兴趣. 下面举几个本质强不定问题的例子,限于篇幅,不具体讨论例子中的非线性项需满足的条件 (可参阅下一节关于 Dirac 方程的有关细节).
•Schrödinger 方程. 考虑
-Δu+V(x)u=f(x,u),u∈H1(n,)
(6)
假设V∈C(3且周期地依赖于x∈n,g(x,u)∈C(3×,). 方程(6)具有抽象形式(1),其中H=L2(n,), 在H中A=-Δ+V是自共轭的,ψ(u)=N(u)(=g(;u))参见文献[11,26-39].在infV<0的条件下, 当0∉σ(A)时,(6)是本质强不定的.
•Hamilton 系统的同宿轨. 考虑 Hamilton 系统,参见文献[15-16,20,22,25,40]
(7)

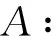
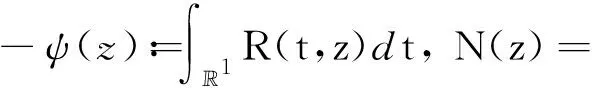
系统(7)可表示为式(1)的形式:
Az=N(z).
•反应扩散系统. 考虑下述(时间依赖)非线性系统参见文献[12,17,28,34,41-44]:
(8)
(t,x)∈×n,G:×n×2m→,L是L2(×n,2m)中的对称稠定算子.求解z=(u,v):×n→2m, 使得z(t,x)→0, (当|t|+|x|→∞). 置
令
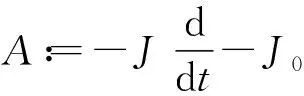
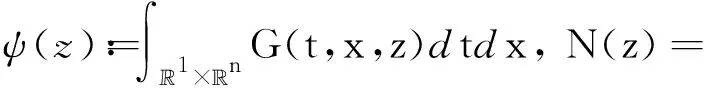
则(8)可表示为(1)形式:
Az=N(z).
特别地,当L=(-Δ)s时就是所谓的分数阶反应扩散系统,参见文献[21].
注2观察对于本质强不定泛函(1),由于一方面σe(A)∩(-∞, 0)≠Ø且σe(A)∩(0, ∞)≠Ø,从而导致E±都是无穷维的子空间,另一方面通常用以处理无界区域上的变分问题,而无界区域上的 Sobolev 型嵌入是非紧的,因之Φ一般不具有紧性(即常说的 Palais-Smale条件),所以问题十分复杂.特别是不能应用Leray-Schauder度以判别所谓的“相交数”问题.在这方面笔者相对系统的工作,其原创点:引入“gage space” (非距离拓扑) 的Lipushitz正规性概念,建立Lipushitz 单位分解;建立局部凸拓扑线性空间上的常微分方程的柯西问题流的存在唯一性这一基础性理论;获得新的形变理论,把无穷维水平集依弱拓扑局部形变到有限维空间中.基于此,笔者得到了一系列新的Minimax 方法, 发展了指标、畴数理论及其他几何拓扑方法,参见文献[5,13,18].
2 非线性 Dirac系统
粒子物理学中出现的Dirac方程是由英国物理学家Paul Dirac提出的一种相对论下的复向量方程,其中×3上自由的(即无外力场)Dirac方程:
-i∂tψ=ic×3→4,
已经被公认为是用于描述带有质量的相对论电子的基本模型.方程中的c是光速,是Planck常数,m是带电粒子的质量,α1、α2、α3以及β是4×4的Pauli矩阵:
此处
这一自由模型很好地给出了自然界许多真实粒子的近似描述.为了更进一步地刻画真实的粒子运动,就必须引入(新的)非线性项.一般说来,在非线性外力场下Dirac方程可表示为
-i∂tψ=ic
(9)
此方程中出现的函数N(x)与ψF(x,ψ)来自于非线性粒子物理中的数学模型,主要用于逼近刻画真实的外力场.其中,非线性耦合项ψF(x,ψ)刻画了量子电动力学中的自耦合作用,给出了一个与真实粒子非常接近的描述.关于非线性项F的例子可以在标量自耦合作用理论中找到,它既可以是多项式型的也可以是非多项式型的函数. 大量的非线性函数已经被公认为是统一场论中合理的基本数学模型.
对于Dirac方程的研究,从变分学的角度讲,人们关心形如ψ(t,x)=exp(iξt/)u(x)的稳态解(也可称为驻波解).于是在研究稳定态问题中,一个自然的假设是
ψF(x,eiξφ)=eiξ,ψF(x,φ).
对所有的ξ∈和φ∈4成立.在此条件下,稳态解ψ满足方程(9)当且仅当函数u满足方程
-ic
(10)
整理后并令α=(α1,α2,α3),
α·
就得到了如下的(一般型)稳态Dirac方程 (a>0):
-iα·u+aβu+M(x)u=Gu(x,u)
(11)
或
-iα·u+aβu+M(x)u=Gu(x,u)
(12)
注3稳态Dirac方程(11)吸引着众多学者的关注.文献中较早研究非线性Dirac方程(11)的工作只是自治系统,即M=ω是常数,G(x,u)=G(u)不依赖于空间变量x(参见文献[45]) 研究所谓Soler模型,即G满足
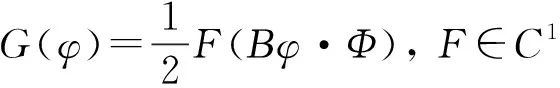
(13)
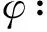
令
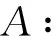
则式(11)呈式(1)的形式.此时σ(A)既无上界又无下界,且一般而言σe(A)∩(-∞,0)≠∅,σe(A)∩(0,∞)≠∅.这表明式(11)是非常强不定的.继续前面的记号:令空间E=E-⨁E0⨁E+由式(3)定义,泛函Φ(u)由式(5)给出.
下面回顾关于非线性Dirac方程研究的主要方面及部分结果.先考虑=1的情形,参见文献[5,13-14,35,45].
(1)关于A的谱, 有下述结论:
-σ(A)=σc(A)=(-a+ω,a+ω), 如果(V1):M(x)≡ω.
-σ(A)=σc(A)是一列两两无交的闭区间的并,如果(V2):M(x)关于xj是Tj>0周期的,j=1,2,3.

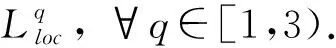
(3)关于非线性,常考虑下述情形:
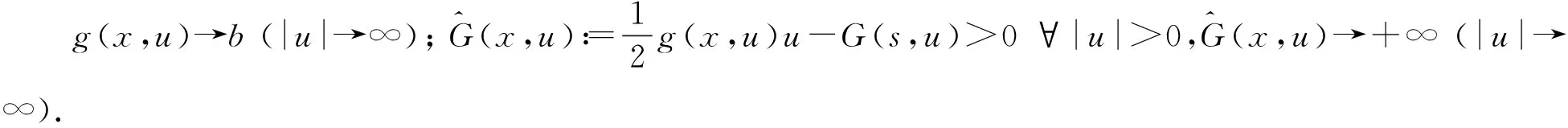
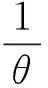
- 临界: 当 |u|→∞时,G(x,u)~|u|3.
- 周期外力场: 即M(x) 和G(x,u)关于xj是Tj>0 周期的,j=1,2,3.
(4)关于解类型, 主要包括:
- 衰减型: 求解u∈H1(3,4) (或u:3→4满足u(x)→0 (当|x|→∞);(x,u)→+∞ (|u|→∞).
- 周期解:u(x+T)=u(x),T=(T1,T2,T3). 此时要求M(x) 和G(x,·)关于x都是T-周期的[32].
α·(-i·g(|w|)w.
在量子力学中,一个很自然的奇异扰动问题就是动力学方程的半经典问题,其物理解释就是对应原理,即当普朗克常数趋于零时所有量子力学的规律将回归于经典力学.作为对应原理的重要体现,量子理论中的两大动力学方程(Schrödinger, Dirac)的解在随着消失过程中的渐进行为尤其值得关注.所谓的集中现象是指:在预先给定的集中集合以外,动力学方程的解随着参数的消失而一致衰减到零.在这样的定义下,从数学上来说,寻找并刻画集中集合成为最本质的问题.
早先对于带小参数的变分问题,学者们主要关注非线性Schrödinger方程的半经典解,获得了丰富的成果.而对于非线性 Dirac 方程的相关问题的研究,因为其研究比前者困难得多,直到2010年才由笔者突破强不定性引起的极大障碍得到第一个结果[19], 引发了一系列后续研究.
记ε=, 利用伸缩变换xεx,式(12)等价于
-iα·u+aβu+Mε(x)u=Gu(εx,u)
(14)
其中Mε(x)=M(εx). 为了反映M的性质,取A0=-iα·+aβ.注意到σ(A)=σc(A0)=(-a,a),因此,L2将有如下的正交分解:
L2=L+⨁L-,u=u++u-
(15)
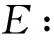
(u,v)=(|A0|1/2u,|A0|1/2v)2
以及诱导范数‖u‖=(u,u)1/2.可以得到:对所有u∈E,
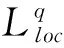
(16)
• 集中于非线性位势的最大点集. 文献[19]考虑
-iεα·w+aβw=W(x)g(|w|)w
(17)
假设(W):infW>0, lim sup|x|→∞W(x) κ=maxW; 利用“山路型”导出、与极限方程的联系、极限方程的性质等. 假设 (W),κ∞<κ, 且g(|w|)~|w|p-2,p∈(2, 3). 文献[19]证明: (1) (存在性)∀ε>0充分小, 式(17)至少有1个最小能量解wε∈s≥2W1,s. (2) (集中性) ∃|wε|的最大值点xε,dist(xε,)→0 (ε→0), 使得 ∀xε→x0, 序列uε(x)=wε(εx+xε)一致收敛于下述极限方程的最小能量解: -iα·u+aβu=κg(|u|)u. • 竞争型位势. 文献[30-31,36]考虑具有线性位势,或同时具有线性和非线性位势的情形: -iεα·w+aβw+V(x)w=W(x)g(|w|)w (18) 其中V,W∈C1(3,), max|V| 不失一般性,设W(xv)=maxx∈W(x),V(xw)=minx∈V(x),并置 文献[30]证明:∀ε>0充分小, 式(18)具有最小能量解wε∈s≥2W1,s满足: -iα·v+aβv+V(x0)v=W(x0)g(|v|)v (19) • 局部最小条件. 前述的半经典结果都要求M(x)=V(x)I4满足所谓“全局”性条件,一个自然的问题就是位势函数M(x)=V(x)I4是否可以摆脱全局性条件. 文献[14]回答了此问题,证明必然存在一个单峰解,且随着的消失该解将集中于V(x)在Λ内的最小值处.即取代假设∃有界开集Ω⊂3使得 得到相应的结论. • Maxwell-Dirac系统. Dirac方程作为描述相对论电子的基本模型,对于真实粒子的运动描述依然存在一定的误差.所谓的这些误差,其来源就是粒子运动所产生的电磁效应对其自身的影响以及周围粒子的相互耦合作用.为了将这样的误差考虑在内,笔者将面对如下形式的复杂方程组Maxwell-Dirac 系统: (20) 其中,向量函数A=(A1,A2,A3):×3→3表示变化的磁场分布,A0=Q:×3→表示变化的电场分布,g代表非线性耦合.A,w遵循电动力学中的Maxwell方程组,真实地刻画出带电粒子高速运动下产生的电磁效应,利用伸缩变换u(x)=w(εx),得到式(20)的等价问题 (21) 其中,Qε(x)=Q(εx),Pε(x)=P(εx),Aε(x)=A(εx),Aε,k(x)=Ak(εx)以及 文献[43]建立了式(23)解的存在性、指数衰减性、集中性. 文献[37]则讨论了它的解的多重性. • Klein-Gordon-Dirac系统. 考虑下述系统 (22) 这里,λ>0表示耦合系数.方程组(22)通过Dirac场ψ与标量场φ之间的Yukawa作用,刻画出Dirac方程与Klein-Gordon方程之间的耦合关系,描述了在介子影响下原子核之间的强作用力.作变换u(x)=φ(εx),V(x)=φ(εx), 式(22)等价于 (23) - 所有基态解的集合在H1(3,4)×H1(3,)是紧的. (i) |φε|有最大点xε,limε→0dist(xε,)=0,使得 (uε,Vε),uε(x)=φε(εx+xε)与在H1×H1中收敛到下极限方程的基态解: (24) • 自旋流形上Dirac方程的分歧现象和边值问题. 设(M,g)是m-维的紧自旋流形,(M)是M上的自旋丛, D:C∞(M,(M))→C∞(M,(M)) 是Atiyah-Singer Dirac算子: 其中,{ej}1≤j≤m是TM上的一组局部正向标准正交基. 又设h:(M)→(M)是保持纤维的非线性映射. ★ 文献[23]考虑下述方程: μDψ(x)=ψ(x)+h(ψ(x)),x∈M (25) 其中,ψ(x)∈C∞(M,(M))代表旋量丛的光滑截面.此方程可看作 Dirac 算子D的摄动特征值问题.在适当条件下证明在原点及无穷远处出现分歧现象. - 对任何 1/μk∈σ(D),k∈, (μk,θ) 是方程(25)的分歧点. - 若 1/μk∈σ(D),k∈,h全连续,在W1/2,2(M,(M))中,h(ψ)=o(‖ψ‖) (‖ψ‖→∞). 则 (μk,∞) 是方程(25)在无穷远处的一个分歧点. 此外,若加强适当对h的假设, 则μk有右邻域λ使得,任给μ∈Λ{μk}, 方程(25)至少有一个非平凡解ψμ使得 ‖ψμ‖→∞ (μ→μk). ★ 文献[24]研究下述边值问题 (假设M具有光滑边界∂M): (26) 这里BCHI记 Chirality 算子,P代表在该边界条件下的Dirac算子. 该文证明了下述结果: ①方程(26)具有至少一个解; ②如果h还是奇的,则方程(26)具有无穷多对解 {±ψk}k, 其相应的能量序列趋于无穷 (k→∞). 前述例子及大量的事实让人们看到,变分方法在交叉科学研究中发挥着十分重要的作用. “所谓交叉学科是指自然科学和社会科学相互交叉地带生长出的一系列新生学科”(钱学森),通常指两个或多个学科之间跨学科的综合研究,是不同领域和不同学科在认识世界过程中,用不同角度和方法为解决共同问题产生的学科交融,经过反复论证和试验而形成的新的科学领域.20世纪下半叶,各类交叉学科的应用和兴起为科学发展带来了一股新风,许多科学前沿问题和多年悬而未决的问题在交叉学科的联合攻关中都取得了可喜的进展.随着越来越多交叉学科的出现及其在认识世界和改造世界中发挥作用的不辩事实,交叉学科在科学领域中的生命力都得到了充分的证明. 交叉科学则是指更为广泛的科学交叉,即自然科学与社会科学的大交叉,探讨的主题是自然科学之间且和社会科学的结合和渗透问题.1985年4 月,在钱学森、钱三强和钱伟长等学者的倡导下,在北京召开了全国首届交叉科学学术讨论会,提出了激动人心的口号:“迎接交叉科学的新时代!”. 一般而言,交叉科学分为四个层次: • 学科的“内部”交叉 交叉学科的最基本的类型即是一个学科内的各个方向的内部交叉.当学科发展到一定程度,子学科的建设呈现一定规模时,学科内部方向的融合交叉可以拓展更多的研究领域,提示整个学科的科学水平. • 学科间的“近距离”交叉 是在不同子学科背景下的合作.如数学与统计学、数学和力学等的交叉,这均属于在一类的学科间的交叉.数学应用于其他学科是20世纪科学发展的突出特点,定量的方法被广泛地应用于几乎所有的学科 (自然科学、社会科学),不断实现真正的科学整体化发展. • 学科间的“远距离”交叉 如数学与中文、人口学与物理学、医学与地质学等等,也出现了学科交叉.学者在研究和探索过程中,有意或无意地发现原来相距很远的学科间有一种可以相互推理或者是互为所用的极妙关系.交叉往往会解决一些较为棘手和尖端的科学问题. • 人们以往所认识的交叉学科,大多是在自然科学学界内或社会科学学界内的研究.近些年来,研究两界间交叉合作日益增多,逐步体现出以“把握学科前沿,促进学科交叉”的导向, 在思想上把社会科学和自然科学放在同等重要的地位. 交叉科学的重要性主要体现在: ①社会进步科学发展需要加强交叉科学. ②学科交叉点往往就是科学新的生长点、新的科学前沿,这里最有可能产生重大的科学突破,使科学发生革命性的变化. ③有利于综合性地解决人类面临的重大问题.交叉科学是自然科学、社会科学、人文科学、数学科学和哲学等大门类科学之间发生的外部交叉,以及本门类科学内部众多学科之间发生的内部交叉所形成的综合性、系统性的知识体系,因而有利于有效地解决人类社会面临的重大科学问题和社会问题,尤其是全球性的复杂问题.这是交叉科学所能发挥的社会功能. ④国家对交叉科学的高度重视. 下面列举一些交叉科学领域.变分理论在研究这些领域的某些方面已经表现出重要作用及强大的生命力,而在某些方面则期待着原始性的创造性的工作出现. ◆ 社会科学方面 • 经济学. 数学在经济学发展中起着重要作用.统计显示,至2008年止的62 位诺贝尔经济学奖中有20位获得过数学学位.大范围变分是研究经济学的一个重要手段. • 上层建筑学. 经济基础决定上层建筑.数学和经济学的交叉自然延展为数学与上层建筑的交叉. • 系统控制. 如优化管理,国防指挥系统,运筹博弈,等. • 复杂系统. 复杂系统理论、预测科学、金融数学与风险管理、信息学、不确定性决策理论与方法. • 哲学. 数学和哲学同是高度抽象的学问,有相同的思考方式,用数学去描述哲学大有可为.例如“无数偶然蕴含必然”,用大数据描述偶然,经数学分析可前瞻必然或掌控必然的趋势. • 文学艺术. 设想把各种描述感情的词藻集成文库,当写诗词小说时输入该感情符号,让电脑自动组合输出成文该多美妙啊.数学的思想、方法和精神对于绘画、做诗具有十分重要的意义. “越往前走,艺术就要科学化,同时科学也要艺术化”(福楼拜).“数学到了最后阶段就遇到想象……于是数学也成了诗”(雨果). ◆ 自然科学方面 • 宇宙学. 宇宙起源、中微子、暗物质与暗能量、多体问题、自旋流形. • (无界)Hamilton控制. • 力学系统. 钱伟长曾说过力学就是变分. 19世纪前历史上最著名的数学家同时也是顶尖的力学家,如19世纪前的阿基米德、牛顿、莱布尼兹、欧拉、拉格朗日、柯西等. 在20 世纪科学日益成为专家在愈来愈窄的邻域内进行着的事业,鲜有如庞加莱、希尔伯特、柯尔莫哥洛夫等同时是数学家和力学家. 1)量子力学. 研究微观粒子的运动规律的物理学分支学科,它主要研究原子、分子、凝聚态物质,以及原子核和基本粒子的结构、性质的基础理论. 量子世界的调控与信息、能源、材料等技术的新突破. 特别如 Schrödinger 方程、Dirac 系统的驻波与行波,描述Bose-Einstein 凝聚及光在非线性介质的传播等. 2)理论力学. 用拉格朗日力学和哈密顿力学的观点处理牛顿力学问题,并加入混沌等较新的内容. 3)电动力学. 主要研究电磁场的基本属性、运动规律以及电磁场和带电物质的相互作用.包括:介质中的场方程和边值问题,有介质存在时电磁波的传播,以及电动力学对超导体、等离子体和晶体的电磁性质的描述. 4)相对论. 关于时空和引力的理论,主要由爱因斯坦创立.奠定了现代物理学的基础.相对论极大地改变了人类对宇宙和自然的“常识性”观念,提出了“同时的相对性”、“四维时空”、“弯曲时空”等全新的概念. 5)热力学与统计物理. 研究热运动的规律和热运动对物质宏观性质的影响.热力学是热运动的宏观理论,统计物理是热运动的微观理论. 宏观量是微观量的某种统计平均值. 6)材料力学. 研究材料在各种外力作用下产生的应变、应力、强度、刚度、稳定和导致各种材料破坏的极限. 7)流体力学. 变分法在研究流体力学方程中的Rayleigh-Taylor线性不稳定问题中起着重要的作用. 针对具有重力场的三维非齐次不可压缩 Navier-Stokes 方程组, 就是用的经典变分法得到解的存在性.其方法还被推广运用到其它更复杂的流体运动,例如,磁流体、粘弹性流、分层可压缩磁流体、 无磁扩散效应的不可压缩磁流体,等等. • 生态学. 以数学的理论和方法研究生态学,它包括生态数学模型、生态系统分析、统计生态学、生态模拟等内容.而今它在理论、实验和应用研究方面都有着很大的进展. • 生命科学. 生命起源、进化和人造生命 • 认知科学. 脑与认知科学及其计算建模 • 随机微分方程的变分方法. • 大数据科学. 建立与应用相应的山路定理. • 杨-米尔斯(Yang-Mills) 存在性(“千禧难题”之五). 又称规范场理论,是研究自然界四种相互作用(电磁、弱、强、引力)的基本理论,是由物理学家杨振宁和米尔斯在1954年首先提出来的.杨-米尔斯提出了杨-米尔斯作用量(规范势的泛函). 作它的变分,就得到纯杨-米尔斯方程. 杨-米尔斯联络是在给定结构群的联络空间上由曲率的平方模定义的泛函的临界点.


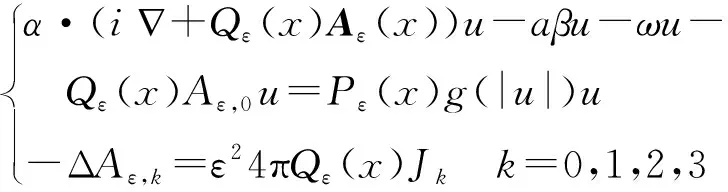
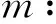
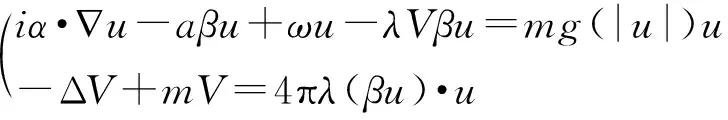

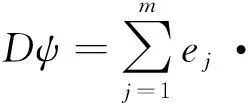
3 交叉科学
