王双炎，李聪，杨玉龙，庞志成，汤晗青



向量式有限元面内逆向转角计算方法

王双炎，李聪，杨玉龙，庞志成，汤晗青

(浙江大学 建筑工程学院，浙江 杭州，310058)

为提高向量式有限元方法的计算效率，以三角形平面固体单元为例，提出一种用边转角法计算逆向运动的面内转角的方法，并将其与常用的质心转角方法进行对比，比较2种方法的计算效率；通过自编程序，分别验证边转角法在计算单元刚体运动、小变形、大变形及复杂结构的变形时的准确性和计算效率。研究结果表明：与质心转角法相比，采用边转角法计算面内逆向转角具有较高的准确度和计算效率，该方法对于常见结构面内逆向转角的计算是可行的、有效的。

向量式有限元；逆向运动；平面三角形单元；计算准确度；计算效率

向量式有限元[1-3](vector form intrinsic finite element, VFIFE)是基于向量力学和数值计算所提出的新型有限元数值计算方法，其核心思想在于将构件离散成若干个质点，通过描述各质点的运动从而对构件整体进行描述。该方法的计算特点在于通过时间积分实现对各点各步的逐步循环计算。由于不存在单元刚度矩阵和矩阵奇异等问题，又无需求解繁杂的非线性方程组，所以，相比传统有限元方法，向量式有限元在计算特殊的非线性问题有着独特的优势。王震等[4-6]从单元形式入手，将向量式有限元理论推广至薄板、薄壳以及四节点实体单元。HOU等[7]在此基础上，推导了八节点正方体单元的向量式有限元应用。在向量式有限元非线性行为研究中，如有关断裂[8-9]、碰撞[10−11]等方面的研究，目前也有了一定的进展。但由于目前还没有商业的向量式有限元软件，一般需要通过Matlab程序实现向量式分析计算，而Matlab自身的运行速度具有一定的局限性。而且越是复杂的结构，划分的单元数越多，所需的计算总时间也越多，因此，提高计算效率就显得尤为重要。YANG等[12]在其研究中阐述了向量式有限元的计算效率。传统的向量式有限元一般采用质心转角法计算逆向转动角度。为了提高计算效率，本文以理论体系较为成熟的三角形平面固体单元[13-15]为例，采用边转角法计算逆向转动角度。HOU等[7,16]虽使用了边转角法进行计算，但未对该方法在计算过程中的计算准确度和计算效率进行详细讨论。为此，本文作者对单元逆向运动过程中，边角转角法与质心转角法2种面内转角的计算方法的计算准确度和计算效率进行比较分析；通过算例验证使用边转角法计算面内逆向转动角度的准确性及其在计算效率方面所具有的优势。

1 向量式有限元平面固体单元理论

1.1 点值描述

传统有限元采用1个有限个单元的集合体来描述求解的结构，而向量式有限元则采用点值描述。这些质点通过相互连接形成单元，建立了质点与单元间的拓扑关系。质点是描述构件受力变形、几何尺寸、空间位置、边界条件的载体。构件在运动过程中，通过描述各质点的位置和速度向量来描述固体构件的整体运动。

每1个质点的运动都遵循牛顿第二运动定律。对于质点而言，m为质点的质量，为质点的空间位置向量，则质点的运动平衡方程可表示为

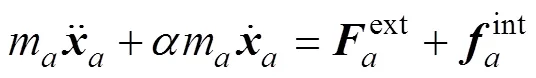
1.2 途径单元

每1个质点的运动过程都是连续的，这些质点的运动轨迹可以表示为以时间为自变量的空间位置函数。在质点运动的全运动周期过程中，用一组时间节点(0，1，2，…，t)将质点的运动轨迹离散成若干微小时间段。在a～b时间段内，若质点的运动均满足连续的时间函数，则称2个时间节点间的时间段为途径单元。

时间点和途径单元可根据结构可能产生的行为进行设定。每1个离散质点连接形成的单元在设定的途径单元内发生的变形均为小变形。当构件有大的几何变形时，整个变形的过程被途径单元离散为许多小变形运动过程的叠加，从而使得描述大变形变得简单。

1.3 逆向运动

为了计算得到单元节点内力，需要从单元节点的整体位移中扣除刚体位移得到节点的纯变形量，进而由虚功原理获得单元节点内力。

在1个途径单元内，平面固体单元的刚体位移由刚体平动和刚体转动2个部分组成。图1所示为1个三角形平面固体单元在a至时刻的途径单元内的刚体位移变化。a时刻为单元基础构型，此时单元节点分别为1a，2a，3a。单元在时刻运动到了图示位置，此时单元节点为1，2和3。图1中，为节点的刚体平移向量(=1，2，3)；2和3为经过逆向平移后的节点；为扣除刚体平移后的节点位移向量。

图1 刚体逆向平移

在局部坐标系下，和a时刻节点的位置向量分别为和a，选取任意一点作为参考点(本文选取1号节点)，将单元平移，使得2个对应参考点位置重合，则参考点经过的逆向平移向量即为单元逆向刚体平移向量：

由此得到扣除刚体平移后的节点变形量为

式中：=2，3。

对单元进行逆向刚体转动。假设逆向转动角度为，则各节点的刚体转动位移为

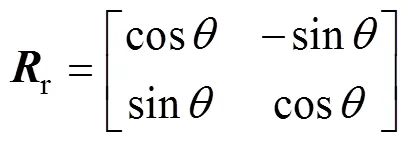
式中：=2，3。

1.4 节点内力计算

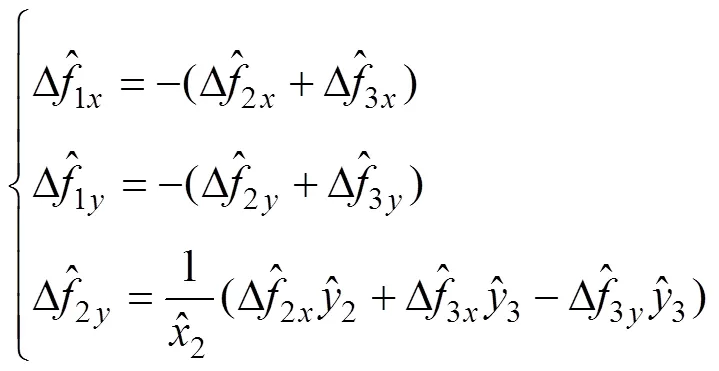
最后，经过正向运动，将局部坐标系下的单元节点内力转换至整体坐标系下：

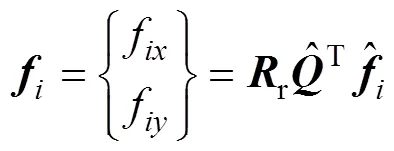
式中：=1，2，3。获得单元节点内力后，即可由中央差分公式实现循环计算。

2 逆向运动方式探究

2.1 面内转角的计算方法与计算精度

由本文第1节的分析可知：求解逆向运动过程中的逆向转动角度至关重要，其计算准确度和计算效率将影响整体计算结果和计算效率。文献[17−18]中，逆向运动过程的面内转角估算值均采用了质心对应转角取平均值的方法进行计算(以下简称质心转角法)，如图2所示。其中，aO和dO分别为单元在a和时刻的质心位置向量；aO与dO分别为a和时刻单元各节点相对于质心的方向向量。(=1，2，3)为节点相对于自身平面单元形心的转动角度。

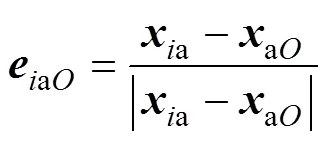
式中：=1，2，3。

在逆向转动面内，取3个节点转动角度的平均值作为逆向转动转角：

“面向传动装置的ABB AbilityTM 状态监测解决方案也是本次ACW的亮点之一。”ABB中国机器人及运动控制事业部负责人李刚表示，“它是业内首个集成化服务，能够将每台设备的关键运行参数集中显示，借助ABB的技术优势，它还能使客户提前了解维护需求，确保设备实现理想运行状态。总而言之，借助ABB AbilityTM 状态监测服务，用户可以更好地掌握如何优化设备运行，减少宕机风险，延长设备寿命，降低成本并且增加收益。”

经逆向运动扣除了单元节点位移中的单元刚体平动和刚体转动后，a基础构架时刻和d时刻虚拟单元间的节点位移仅包含单元纯变形和残余转动变形。这个残余转动变形来源于单元变形的不均匀分布。而向量式有限元在设定途径单元时，保证每一个途径单元内单元变形均为小变形，单元变形接近均匀变形，这就使得单元纯变形对节点内力影响为一阶量，而残余变形的影响相对纯变形的影响为高阶量。

因此，可采用任意方法对面内转动角度进行估算，只需要满足以下基本条件：假设单元的纯变形为0时(单元仅存在刚体运动)，估算方法得到的转角应为正确的转动角度。例如，当固体平面单元发生角度为的刚体转动且单元变形量为零时，根据质心转角估算法，1=2=3=，=成立，是正确的刚体转角。

基于上述理论，本文建议使用另1种方法估算面内转角，即边转角计算法(见图2(b))。三角形平面固体单元经历了逆向平动后，参考点1已重合。此时，需进一步扣除逆向刚体转动。与逆向刚体平动一样，任取包含作为逆向刚体平移的参考点的单元一边作为参考边，以参考边的转动角度作为刚体逆向转动角度。图2中选取的边为节点1和3所形成的单元边，则有：

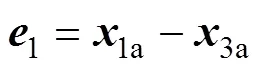
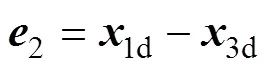
式中：1为单元在a时刻节点1和节点3所形成的边向量；2为单元在时刻经逆向刚体平移后，节点1和节点3所形成的方向向量。假设单元仅发生刚体运动而没有纯变形，且单元刚体转动角度为，此时，根据边角计算法，=成立，满足面内转角估算方法的基本条件。

图2 面内逆向转角计算方法对比

2.2 不同计算方法的计算效率

向量式有限元方法在求解式(1)的运动方程时，通常采用显式时间积分法中的中央差分法。

无初始条件下的中央差分表达式为

有初始条件下的中央差分表达式为

式中：+1为第+1步的节点位置向量；为质点质量；和分别表示节点所受到的外力和节点内力；为时间步长；1=1/(1+/2)；2=1/(1−/2)。

除此之外，在向量式有限元中，还有一项重要的工作即估算临界步长。在平面三角形固体单元内，材料轴向应力刚度一般较高，分析单元轴向运动时所需的时间步长较短，因此，一般以单元轴向运动为基准对计算过程中的临界步长进行考量。将单元简化成长度为的质点和劲度系数为的弹簧单自由度体系，材料的弹性模量为，横截面积为，在外力作用下，构件长度变化量为，则有：

=(23)

由此可见，在材料参数相同的情况下，离散质点数越多，质点连接而成的单元网格越小，所能取得的临界步长越小。向量式有限元作为一种在处理碰撞、断裂、接触等结构大变形问题时具有独特优势的新型数值计算方法，往往需要将构件离散成数量庞大的质点组来满足对构件变形精确描述的要求。而在内力计算过程中，为避免内力误差迅速积累而出现结果发散现象，尤其是在使用显示时间积分求解运动方程的情况下，时间增量很小，迭代计算的循环步数一般很庞大，此时，计算效率的提升就显得尤为重要。

图3所示为不同计算方法的计算流程图。相较于传统的质心转角计算方法，边转角计算法无需计算单元质心位置，向量计算量也明显较少。对于1个时间步长内的1个单元而言，在面内逆向转角计算步骤中，质心转角算法需完成10次向量加减运算、8次向量乘法运算、3次向量点乘运算、6次向量求模运算、2次标量加减运算以及1次标量乘法运算；边转角法仅需完成2次向量加减运算与1次向量乘法运算。由计算机工作原理可知，边转角计算法可以有效提高计算机的运行速度。

3 算例验证

从上述分析可以看出，取质心与节点的向量转角平均值作为逆向转动角度和以边向量转角为基准作为逆向转动角度均是可行的。同时，在计算效率方面，由于边转角法的计算量更小，在多质点多单元的情况下更具优势。本节通过自编Matlab程序进行算例模拟，对上述边转角理论的正确性进行验证。

3.1 单元刚体运动

由表1可知：2种方法在处理单元刚体运动问题时，均具有较高的准确性。当单元旋转10圈时，质心转角法所用时间为2.7 s，边转角法所用时间为2.2 s。

3.2 正方形薄板受压问题

正方形薄板示意图及单元划分如图5所示。由图5(a)可见：正方形薄板对角受到均布压力荷载的作用，荷载沿垂直于平面的薄板厚度方向均匀分布，为2 N/m。正方形薄板对角线长=4 m，板厚0.1 m，弹性模量=1×1011Pa，泊松比=0。

由于结构具有对称性，只需取1/4部分作为分析对象。由图5(b)可见：构件的1/4被离散成6个质点，质点间互相连接形成共4个单元。将向量式有限元分析结果与传统有限元分析结果进行对比，结果如表2所示。由表2可以看出：在小变形情况下，2种面内转角计算方式的向量式有限元分析结果均与传统有限元的理论值较符合。质心转角法所用时间为2.2 s，边转角法所用时间为1.8 s。

图3 不同计算方法流程图

图4 单元刚体转动

图5 正方形薄板示意图及单元划分

3.3 悬臂梁自由端受集中荷载作用

在Euler−Benoulli梁理论[19]中，悬臂梁端部受集中荷载作用发生剧烈变形是经典的非线性有限元算例，该算例常被用于验证非线性算法理论的正确 性[20−23]。悬臂梁算例示意图如图6所示。悬臂梁长=10 m，梁高=1 m，梁厚为1 m。构件离散成544个质点，以三角形平面单元形式相互连接。材料弹性模量=10 Pa，泊松比=0。当外荷载以荷载因子/2(其中，为悬臂梁横截面的惯性矩)来衡量时，此时悬臂梁变形为大变形。由于该算例是拟静力问题，荷载加载形式取斜坡加载方式。同时，施加虚拟阻尼使结果收敛，取虚拟阻尼系数=10.0。使用质心转角计算法和边转角计算法分别进行计算，验证大变形情况下理论的正确性。

悬臂梁荷载施加点竖向位移和横向位移对比分别如表3和表4。表3和表4中，ABAQUS的单元划分方式均与算例的相同。由表3和表4可知：对于质心转角法和边转角法2种不同的逆向转动计算方法，其自由端在竖直和水平方向上的位移均与理论结果较吻合，2种方法得到的结果之间的差异也很小。即使是当荷载因子达到10这样的高度非线性情况下，依然能取得理想结果，验证了本文第3节提出的边转角计算方法的计算精确性。在计算效率方面，质点转角法最终所用时长为878 s，而在相同情况下，边转角法所用时长为779 s。

表1 节点坐标对比

表2 节点位移对比

图6 悬臂梁算例示意图

表3 悬臂梁荷载施加点竖向位移对比

表4 悬臂梁荷载施加点水平位移对比

3.4 半圆弧结构受力大变形

图7所示为半圆弧结构示意图，圆弧底部两端完全固定。圆弧外径1=21 m，内径2=20 m，材料弹性模量为10 Pa，泊松比为0.25。将结构分别离散成108，318和860个质点进行计算。半圆弧顶部位置施加1个竖直向上的集中荷载。由于该问题是1个拟静力问题，荷载加载方式同样采用斜坡加载方式。取虚拟阻尼系数=10.0。构件将在荷载作用下发生 大变形，验证工程结构条件下边转角计算方法的正 确性。

为验证除荷载施加点之外，圆弧拱所离散成的其他节点位移的正确性，分别选取荷载为1.0 N和3.5 N，观察圆弧拱拱肋上沿部分其他质点产生合位移后连接所成的拱肋变形，如图8所示。同时，选取荷载施加质点进行定量分析。图9(a) 所示为圆弧结构离散为不同质点数情况下荷载施加点的位移与荷载的曲线(由于质心转角法和边转角法的结果差距极小，图8和图9(a)仅展示了边转角法的结果)，并将结果与商业通用有限元软件ABAQUS分析结果进行对比(其中，圆弧结构被离散成5 992个三角形单元)。

图7 半圆弧结构示意图

荷载/N：(a) 1.0; (b) 3.5

由图9(a)可知：圆弧顶点将在荷载作用下先发生非线性位移变化；随着荷载的增加，顶点两边的弧形结构逐渐由曲线变为直线，位移−荷载的变化又重新趋于线性相关；自编向量式有限元程序的分析结果与ABAQUS显示的位移变化趋势相吻合。随着离散质点数的增加，顶点位移逐渐接近ABAQUS非线性有限元分析结果；且在相同的单元划分情况下，向量式有限元计算结果也与ABAQUS计算结果相吻合。

由上述分析可以看出：在保证计算准确度的前提下，边转角法较质心转角法有着更高的计算效率。由于向量式分析的特点，为了获得更精确的结果，需要将结构离散成更多的质点以达到更精确描述结构的目的。此时，运用边转角法进行计算所能节省的绝对时间会更多。

图9 半圆弧结构算例计算结果

图9(b)所示为不同质点数下Matlab程序对于2种方法所需的平均计算时间。由图9(b)可知：对于3种不同离散情况，边转角法相较于质心转角法都能节省时间12%～15%；当结构离散成860个质点时，2种方法的绝对计算时差可达约360 s。

4 结论

1) 为提高向量式有限元的程序计算效率，基于向量式有限元的基本理论和假定，采用边转角法计算单元在逆向面内转动过程中的逆向转角。

2) 通过自编的Matlab程序算例对单元刚体运动、小变形、大变形、复杂结构4种情况进行了验算，计算结果表明边转角法在保证较高计算准确度的前提下，相较于传统的质心转角法计算效率更高。

[1] TING E C, SHIH C, WANG Y K. Fundamentals of a vector form intrinsic finite element: Part 1. Basic procedure and a plane frame element[J]. Journal of Mechanics, 2004, 20(2): 113−122.

[2] TING E C, SHIH C, WANG Y K. Fundamentals of a vector form intrinsic finite element: Part II. Plane solid elements[J]. Journal of Mechanics. 2004, 20(2): 123−132.

[3] SHIH C, WANG Y K, TING E C. Fundamentals of a vector form intrinsic finite element: Part III. Convected material frame and examples[J]. Journal of Mechanics. 2004, 20(2): 133−143.

[4] 王震, 赵阳, 胡可. 基于向量式有限元的三角形薄板单元[J]. 工程力学, 2014, 31(1): 37−45. WANG Zhen, ZHAO Yang, HU Ke. Triangular plate element based on vectored finite element[J]. Engineering Mechanics, 2014, 31(1): 37−45.

[5] 王震. 向量式有限元薄壳单元的理论与应用[D]. 杭州：浙江大学建筑工程学院, 2013: 80−85. WANG Zhen. The theory and application of a vector finite element thin shell element[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2013: 80−85.

[6] 王震, 赵阳, 杨学林. 基于向量式有限元的实体结构非线性行为分析[J]. 建筑结构学报. 2015(3): 133−140. WANG Zhen, ZHAO Yang, YANG Xuelin. Nonlinear behavior analysis of solid structure based on vector finite element method[J]. Journal of Architectura, 2015(3): 133−140.

[7] HOU Xiangying, FANG Zongde. Solid structure analysis with large deformation of eight-node hexahedral element using vector form intrinsic finite element[J]. Advances in Structural Engineering, 2018, 21(6): 852−861.

[8] DUAN Y F, WANG S M, WANG R Z, et al. Vector form intrinsic finite element based approach to simulate crack propagation[J]. Journal of Mechanics, 2017, 33(6): 797−812.

[9] HOU Xiangying, FANG Zongde, ZHANG Xijin, et al. Static contact analysis of spiral bevel gear based on modified VFIFE (vector form intrinsic finite element) method[J]. Applied Mathematical Modeling, 2018, 60: 192−207.

[10] XU Leige, LIN Mian. Numerical modeling of the configuration of a long-distance free-spanning submarine pipeline on an uneven seabed[J]. International Journal of Offshore and Polar Engineering, 2017, 27(1): 102−111.

[11] WU T Y. Dynamic nonlinear analysis of shell structures using a vector form intrinsic finite element[J]. Engineering Structures, 2013, 56: 2028−2040.

[12] YANG Yulong, CHENG J J R, ZHANG Tuqiao. Vector form intrinsic finite element method for planar multibody systems with multiple clearance joints[J]. Nonlinear Dynamics, 2016, 86(1): 421−440.

[13] TORNABENE F, FANTUZZI N, BACCIOCCHI M, et al. Mechanical behavior of damaged laminated composites plates and shells: higher-order shear deformation theories[J]. Composite Structures, 2018, 189: 304−329.

[14] 刘人怀, 薛江红. 复合材料层合板壳非线性力学的研究进展[J]. 力学学报, 2017, 49(3): 487−506. LIU Renhuai, XUE Jianghong. Research progress in nonlinear mechanics of laminated composite plates and shells[J]. Journal of Mechanics, 2017, 49(3): 487−506

[15] 韩强.高等板壳理论[M]. 北京: 科学出版社, 2002: 216. HAN Qian. Advanced theory of plates and shells[M]. Beijing: Science Press, 2002: 216.

[16] XU Leige, LIN Mian. Analysis of buried pipelines subjected to reverse fault motion using the vector form intrinsic finite element method[J]. Soil Dynamics and Earthquake Engineering, 2017, 93: 61−83.

[17] 王震, 赵阳, 杨学林. 薄壳结构的向量式有限元屈曲行为分析[J]. 中南大学学报(自然科学版), 2016, 47(6): 2058−2064. WANG Zhen, ZHAO Yang, YANG Xuelin. Vector form intrinsic finite element method for buckling analysis of thin-shell structures[J]. Journal of Central South University of Science and Technology, 2016, 47(6): 2058−2064.

[18] 底大钧. 三维空间柔性杆件的三角单元向量式有限元模型研究及仿真[D]. 哈尔滨：哈尔滨工程大学理学院, 2017: 24−31. DI Dajun. Research and Simulation of triangular element vector finite element model for three-dimensional flexible members[D]. Harbin：Harbin Engineering University. College of Science, 2017: 24−31.

[19] MATTIASSON K. Numerical results from large deflection beam and frame problems analyzed by means of elliptic integrals[J]. International Journal for Numerical Methods in Engineering. 1981, 17(1): 145−153.

[20] 张鹏飞. 结构破坏行为的数值模拟计算方法研究[D]. 杭州：浙江大学建筑工程学院, 2016: 84−85. ZHANG Pengfei. Study on numerical simulation method for structural failure behavior[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2016: 84−85.

[21] 罗尧治, 杨超. 求解平面固体几何大变形问题的有限质点法[J]. 工程力学, 2013, 30(4): 260−268. LUO Yaozhi, YANG Chao. Finite particle method for solving large deformation problems in plane solid geometry[J]. Engineering Mechanics, 2013, 30(4): 260−268.

[22] El-Abbasi N, Meguid S A. A new shell element accounting for through-thickness deformation[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 189(3): 841−862.

[23] SZE K Y, CHAN W K, PIAN T. An eight-node hybrid-stress solid-shell element for geometric non-linear analysis of elastic shells[J]. International Journal for Numerical Methods in Engineering, 2002, 55(7): 853−878.

Research on reverse rotation angle calculation method of vector form intrinsic finite element in plane

WANG Shuangyan, LI Cong, YANG Yulong, PANG Zhicheng, TANG Hanqing

(College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China)

In order to improve the calculation efficiency of vector form intrinsic finite element (VFIFE), the side-angle-method for calculation of the reverse rotation angle of the triangular plane solid element reverse motion was proposed. By comparing the side-angle-method with the commonly used centroid-angle-method, the calculation efficiencies of these two methods were studied. The accuracy and efficiency of the side-angle-method in calculating the rigid body motion, the small deformation, the large deformation and the deformation of complex structure were discussed and verified by examples using the self compiled program. The results show that compared with conventional centroid- angle-method, the side-angle-method has good computation accuracy and computational efficiency, and it is feasible and effective for calculation of the reverse rotation angle of common structures.

vector form intrinsic finite element; reverse motion; planar triangular element; calculation accuracy; calculation efficiency

TU33+9

A

1672−7207(2019)05−1135−09

10.11817/j.issn.1672−7207.2019.05.017

2018−06−19；

2018−08−19

国家水体污染控制与治理科技重大专项(2017ZX07201004)(Project(2017ZX07201004) supported by the Major Science and Technology Program for Water Pollution and Treatment)

杨玉龙，博士，讲师，从事市政工程安全分析研究；E-mail: yulongy@zju.edu.cn

(编辑 伍锦花)