☉江南大学附属实验中学 胡德林

☉江南大学附属实验中学 黄 静

数学模型（数学模型：对于现实世界的一个特定对象，为了一个特定的目的，根据特有的内在规律，做出一些必要的简单假设，运用适当的数学工具，得到一个数学结构）为我们提供了一种解决问题的方法和手段，一把开启问题大门的钥匙，它把数学和生活紧密联系起来，使我们有了一双发现生活中的数学的眼睛，是解决实际问题的一种有效工具，它的运用，让我们感受到数学无处不在，感受到生活与数学息息相关.要能更好地学习和生活，我们必须学会数学的运用，培养应用能力.古人曰：“授人以渔，不如授人以渔”，我们要教会学生学习，教会学生学习的方法和解决问题的能力远比教给学生知识更重要，模型的运用更好地体现了数学运用的广泛性和灵活性，更有利于培养学生的应用能力.现就初中数学课本中出现的一个数学模型的运用，谈谈数学应用能力的培养策略.

原始模型问题呈现：

将军饮马问题：如图1，据说，在古希腊有一位聪明过人的学者，名叫海伦.有一天，一位将军向他请教了一个问题：从A地出发到河边MN饮马，然后回到B地，走什么样的路线最短？如何确定饮马的地点？

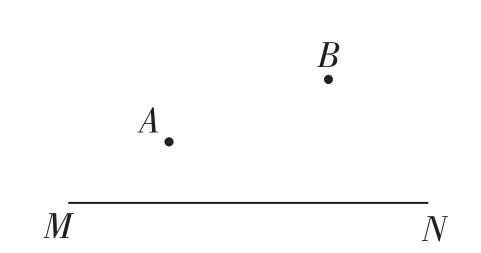
图1

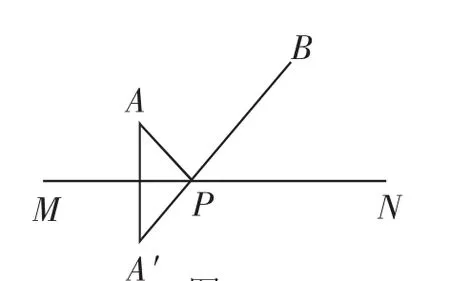
图2

海伦给出的解决方法：如图2，作点A关于直线MN的对称点A′，连接A′B，交直线MN于点P，则P点所在位置即为将军饮马的地点.

应用能力培养策略1：教会学生阅读和分析，弄清问题的本质，提炼数学模型

上面的问题是一个实际问题，我们通过分析、梳理，发现其本质就是关于两个点和一条直线的问题，找出了关键的要素，就可以将它提炼成一个简洁的数学模型.

这个问题模型可以提炼为：已知两个定点A、B和一条定直线MN的问题.

通过这样的提炼，建立起了如图2所示的数学模型，学生更加容易理解、掌握和运用.

在教学过程中，通过引导学生对内容进行认真细致的阅读、理解、分析、领悟，弄清来龙去脉，抓住问题的本质和关键，提炼出数学模型，做到一针见血.

应用能力培养策略2：教会学生总结和归纳，洞察问题的真相，掌握模型的变化

模型运用一：在平面图形中的运用

（一）在三角形中的运用：与三角形的特殊性质融合.

问题1：如图3，在等边△ABC中，AB=6，N为AB上一点，且AN=2，∠BAC的平分线AD交BC于点D，M是AD上的动点，连接BM、MN，则BM+MN的最小值是______.

图3

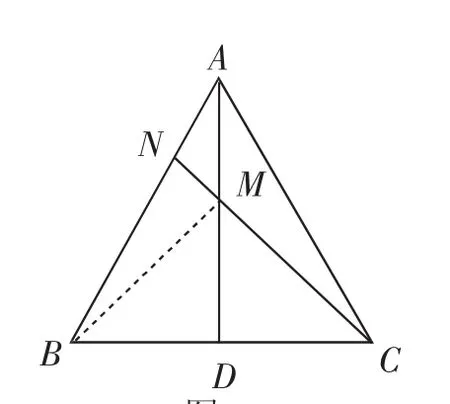
图4

模型提炼：在这个问题中，B、N是两个定点，AD是定线，要求在AD上确定一点M.

解决方法：如图4，根据模型，根据等边三角形的性质，因为点B与点C关于AD对称，所以只要连接CN，交AD于点M，此时M点就满足BM+MN的值最小.（改变等边三角形为等腰三角形，同样可以这样处理）

（二）在正方形中的运用：与正方形性质的融合.

问题2：如图5，E为正方形ABCD的边AB上一点，AE=3，BE=1，P为AC上的动点，则PB+PE的最小值为______.

模型提炼：在这个问题中，B、E是两个定点，AC是定线段，要求在AC上确定一点P.

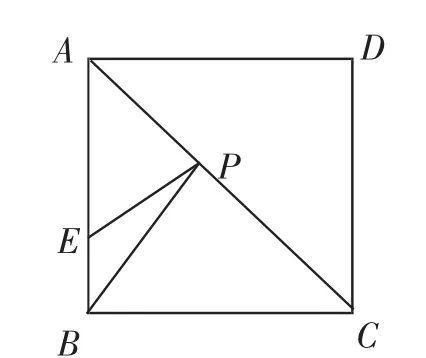
图5

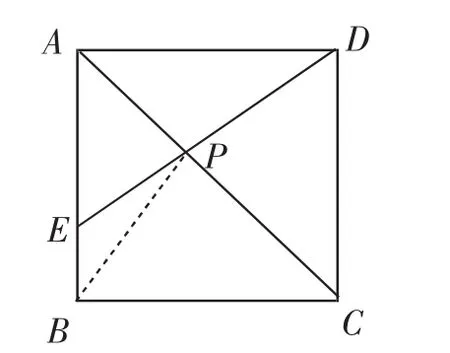
图6

解决方法：如图6，根据模型，因为点B与点D关于AC对称，所以只要连接BD，交AC于点P，此时PB+PE的值最小.（此题中的正方形也可以改为矩形、菱形）

（三）在圆中的运用：与圆的性质的融合.

问题3：如图7，已知⊙O的直径CD为2，弧BC的度数为60°，点A是弧BC的中点，在直径CD上作出点P，使BP+AP的值最小，则BP+AP的最小值为______.

模型提炼：如图7，在这个问题中，A、B是定圆⊙O上两个定点，直径CD是定线段，要求在线段CD上确定一点P，使BP+AP的值最小.

图7

图8

解决方法：如图8，根据模型，只要过点A作AA′⊥直径CD，交⊙O于点A′，则A′就是点A关于CD的对称点，连接A′B，交CD于点P，此时点P就满足BP+AP的值最小.

模型运用二：在函数图像中的运用

（四）在一次函数中的运用：与坐标系的融合.

问题4：如图9，已知两点A（-1，3）、B（3，5），点P为x轴上一个动点.当PA+PB的值最小时，求点P的坐标.

模型抽取：在这个问题中，A、B是两个定点，x轴是定直线，要求在x轴上确定一点P.

解决方法：如图10，作点A（或B）关于x轴的对称点A′（或B′），连接A′B（或B′A），交x轴于点P，此时P点就满足PA+PB的值最小.

（五）在二次函数中的运用：与二次函数的性质融合.

图9

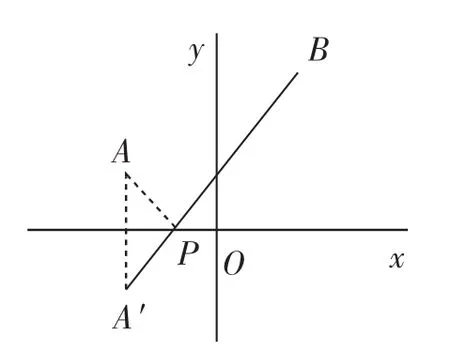
图10

问题5：如图11，抛物线y=ax2+bx+c的对称轴为直线x=-3，该抛物线交x轴于A、B两点，交y轴于点C（0，4），以AB为直径的⊙M恰好经过点C.

（1）求这条抛物线所对应的函数关系式.

（2）设⊙M与y轴的另一个交点为D，请在抛物线的对称轴上求作一点E，使得△BDE的周长最短.

模型抽取：在本题第（2）问中，由于△BDE的周长=BD+BE+DE，而BD的长是定值，所以要使△BDE的周长最短，就是要使BE+DE最短，从而就转化为模型问题.在这个模型中，B、D是两个定点，抛物线的对称轴是定直线，要求在对称轴上确定一点E.

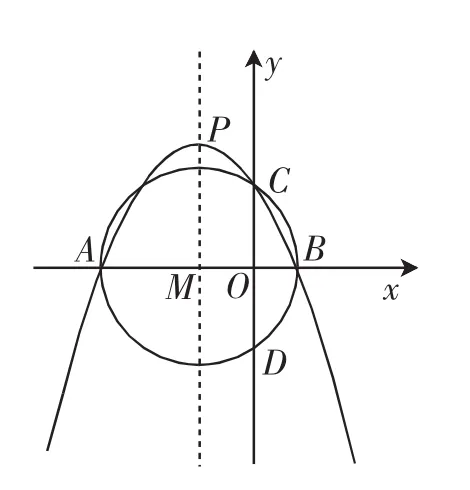
图11

图12

解决方法：如图12，由抛物线的性质，知点B关于抛物线的对称轴的对称点就是点A，所以连接AD交抛物线的对称轴于点E，此时点E就满足BE+DE最短，从而△BDE的周长也就最短.

上面的几个问题展现了模型在不同的几何图形中以不同的变换形式呈现，但只要我们细心观察，认真归纳总结，对情景进行梳理、对问题进行提炼，就能发现这些问题无非是给原始模型换上了不同的外衣，使模型出现在不同的场合中，“人还是那个人，物还是那个物”，只是不变中的变化，变化中的不变，万变不离其宗，仍然是两个定点和一条定直线的问题，达到了一通百通.

应用能力培养策略3：教会学生转化思想，把握问题的本质，突破模型的空间

模型运用三：在立体图形中的运用：圆柱体中的运用与圆柱体性质的融合

问题6：有一圆柱形食品盒，它的高等于16cm，底面直径为20cm，蚂蚁爬行的速度为2cm/s.

（1）如图13，在盒内下底面的A处有一只蚂蚁，它想吃到盒内对面中部点B处的食物，那么它至少需要多少时间？（盒的厚度和蚂蚁的大小忽略不计，结果可含π）

图13

图14

（2）如图14，在盒外下底面的A处有一只蚂蚁，它想吃到盒内对面中部点B处的食物，那么它至少需要多少时间？（盒的厚度和蚂蚁的大小忽略不计，结果可含π）

模型提炼：此题的第（2）问只要将圆柱体沿侧面展开（如图15），问题就转化为已知两个定点A、B和定直线CD，在直线CD上找一点P，使得PA+PB最短.

解决办法：如图16，将圆柱体沿侧面展开，得到长方形，其中A、B两点是定点，线段CD是定线段，要求在CD上确定一点P，使PA+PB最短.所以对照模型很容易想到……

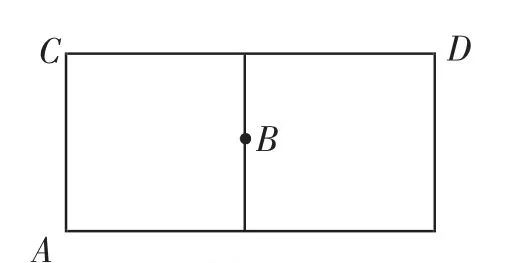
图15

图16

此问题看似与模型无关，模型是在平面图形中的运用，而此问题是在立体图形中的运用，但只要将圆柱体沿侧面展开，就将立体图形转化成了平面图形，呈现在我们面前的就是模型的真面目，揭开面纱就显出了真相，只是模型的转化而已，实现了举一反三.

应用能力培养策略4：教会学生类比延伸，利用问题的联系，实现模型的扩展

模型运用四：模型外延运用：类比推理、运用延伸

问题7：如图17，台球桌面上有如图所示的母球A和红球B，现要将母球A先击打台球桌面的边沿CD后反弹击中红球B，画图说明击打的线路.

模型提炼：此题与模型问题没有本质的区别，都是用对称的方法解决，类比模型问题就能找到答案.

图17

图18

解决办法：如图18，作点A关于直线CD的对称点A′，连接A′B，交直线CD于点P，则只要母球A击打桌边点P处，反弹后就会击中目标红球B.

此问题看似与模型不同，但通过将问题与模型进行对比，发现其与模型问题的本质基本一样，思想相同也相通，运用模型方法，轻易就将其解决.类比的思想、创新的延伸，使模型扩容，帮助我们解决了与之相近的问题，真正做到触类旁通.

数学模型给我们提供了一种解决问题的方法和有效手段，学生在建模、观模、用模和思模的过程中培养了：学习习惯、观察视角、思考方法、思维方式、探索精神和创新能力，提高了数学应用能力，掌握了开启数学问题的“钥匙”，感受到了学习数学的轻松，收获了学习数学的成功，体会到了学习数学的乐趣，增强了学习数学的信心，进而激发了学习数学的兴趣、探究数学的热情.W