平面向量问题的几种处理策略
2019-04-24安徽蒋玉芳张道梅
安徽 蒋玉芳 张道梅
在以往高考中,从平面向量的命题形式可以看出,整个命题过程紧扣课本,重点突出,有时考查单一知识点,有时通过知识的交汇与链接,全面考查平面向量的有关概念、线性运算、数量积及坐标运算等内容.试题难度多为容易题或中档题,少数为选择或填空的压轴题,尤其是近几年的高考和模拟考试中,平面向量难度有所提升,难点多为求解数量积的取值范围、模的取值范围等问题,与其关联的知识点有函数、直线与圆、基本不等式等,题目综合性比较强,大多数学生求解起来相对困难.那么对于这类问题有什么好的处理策略吗?下面本文将呈现出针对该难点的几种处理策略.
【策略一】基底法
此法所涉及的知识点是平面向量的线性运算及平面向量基本定理,即将题目涉及的所有向量,通过线性运算统一成两个不共线的向量,即“多元”变“少元”.这样处理的好处是使题干的条件所表达的含义更“透明”,思路更清晰,性质运用得更合理.具体的解题步骤是:①通过题干合理选取基底;②利用线性运算,统一向量;③结合已知建立等量关系或函数关系等即可求解.
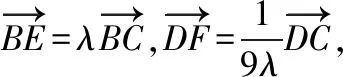
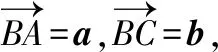
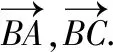
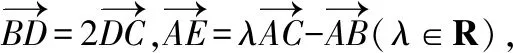

【策略二】构造平面直角坐标系
平面向量是连接代数与几何的桥梁,尤其是平面向量的坐标运算的引入,使得向量与代数的互换运算更是深入人心.一些基于考查向量和代数的互换运算的好题应运而生,这些题目绝大多数都有一个很显著的特征:已知某两个向量所成角.通过这个已知即可建立平面直角坐标系进行求解.具体解题步骤是:①通过题干,合理建系;②将所有向量转化为坐标形式;③利用向量的坐标运算公式和法则对原题进行转化与化归;④在最后的计算时,往往需要借助函数、基本不等式、平面几何等知识方可求解.
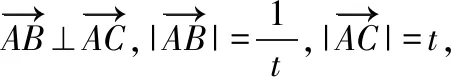
( )
A.13 B.15
C.19 D.21
【解析】以A为坐标原点,建立平面直角坐标系,如图所示,
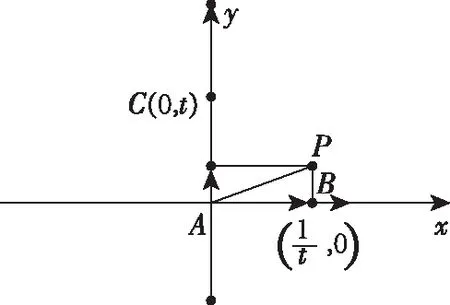
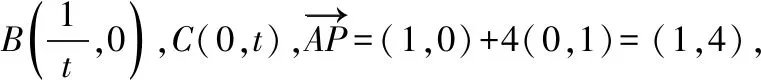
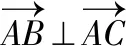
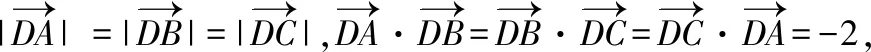
( )
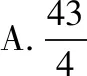
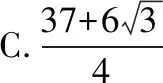
【答案】B.
【策略三】构造图形
在策略二中,谈到平面向量是连接代数与几何的桥梁,也已经了解了向量与代数之间是如何转换的,那么向量与几何之间又是通过什么进行转化的呢?一种转化方式是通过平面向量的几何意义“构造平面图形”,使问题图形化,此种转化称为“形化”.而对于平面向量中有关最值问题通过“形化”后, 问题更具有直观性,即可借助于平面图形的特征直接进行判断.此法具体解题步骤是:①将题干向量用有向线段表示;②通过已知构造图形;③判断动点轨迹;④利用动点轨迹的特征即可求解.
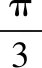
( )
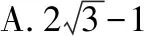
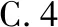
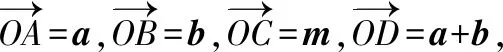
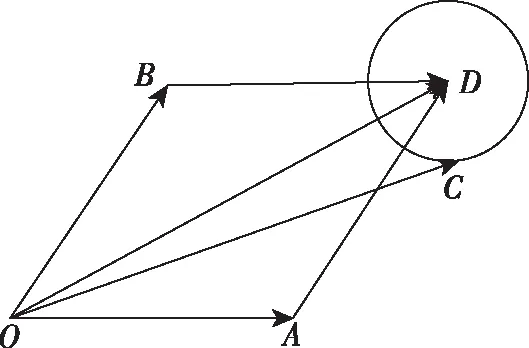
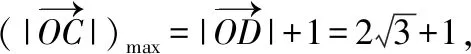
【评注】通过此题可以发现,利用平面图形解决向量问题更清晰、更简洁.而此法需要学生对平面向量的几何意义和一些特殊的平面图形特征的熟练掌握,同时对学生空间想象能力也有一定的要求.
【变式3】(2017·浙江宁波2模)已知|a|=|b|=1,a与b夹角为90°,若c满足(a-c)(b-c)=0,则|c|的最大值是________.
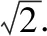
【策略四】极化恒等式
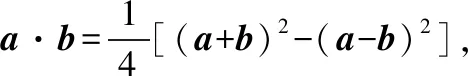

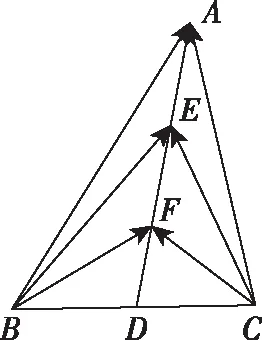
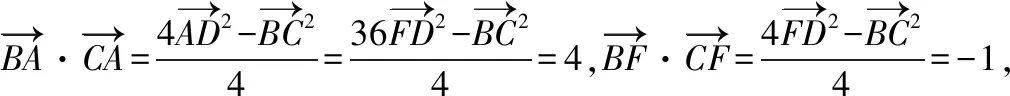
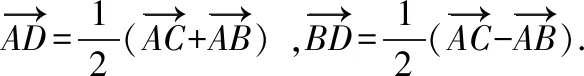
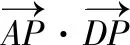
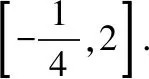
【策略五】利用等和线

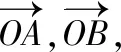
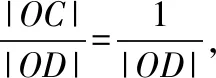
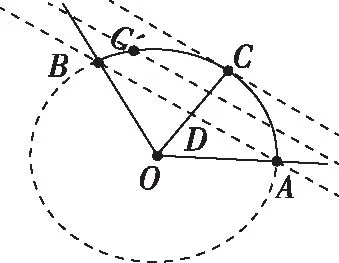
【评注】此法和“极化恒等式”有异曲同工之处,都源于教材,又高于教材,其本质是平面向量共线基本定理的推论和数乘向量.同时此法也考查了数形结合思想.

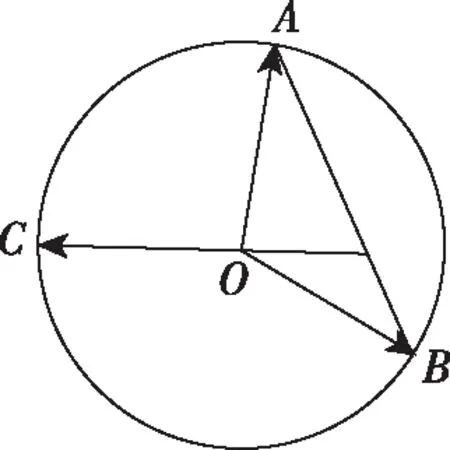
( )
A.1 B.2
【答案】C.

【答案】[-2,-1).
【策略六】利用平面向量数量积的几何意义
利用平面向量数量积的几何意义求解平面向量数量积问题,具有直观性和简捷性的特点,同时它具有的灵活性也使得它不易被掌握,但用好向量的数量积的几何意义能使和数量积有关求值、求最值、求范围等问题的解决变得更加简单.
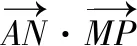
【解析】过M点作AN的垂线,垂足为D,如图所示,
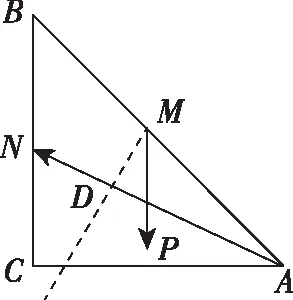
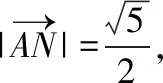
【评注】此题如果不用向量数量积的几何意义同样也可得到正解,但可能稍显麻烦,用几何意义来解则更加简洁、更加直观,在计算方面只需着力计算长度和夹角的余弦值,但要注意先判断所求向量的夹角的情况,若夹角为钝角,则数量积为负;若夹角为锐角,则数量积为正;若夹角为直角,则数量积为零.
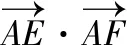
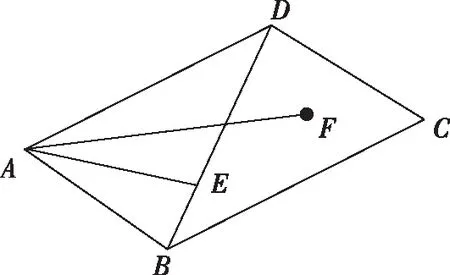
【答案】[9,18].
【策略七】换元法
换元法在函数、多元变量最值、平面解析几何初步中的应用耳熟能详,但在平面向量中,却不能被熟知,而换元法更能有效地将平面向量、代数、几何有机结合,完美地体现了向量这个重要的解题工具.在向量中换元法主要体现在两种换元思想:①构造新向量思想进行换元;②利用代数思想进行换元.在此笔者重点谈“利用代数思想进行换元”,此思想主要解决和向量模有关的问题.具体应用如下:
【例7】(2017·浙江卷·15)已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是________,最大值是________.
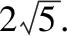
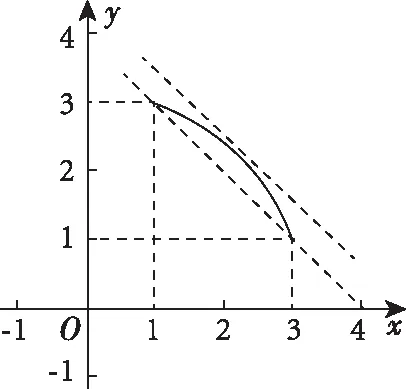
【评注】此法先对|a+b|,|a-b|进行换元,再对|a+b|=x,|a-b|=y两边平方,最终转化为直线z=x+y与曲线x2+y2=10(x,y∈[1,3])的位置关系,完美地诠释了向量是连接代数和几何的桥梁.但利用此法,有一个易错点,是换元变量的范围问题,如本题中的x,y的范围.
【变式8】(2018·浙江丽水一模)已知|m|=2,|m+2n|=2,则|2m+n|+|n|的最大值为________.