周俊屹，郑 霜

(重庆师范大学 数学科学学院，重庆 401331)

0 引 言

众所周知，在经济管理、工程设计、生态保护与道路交通运输等领域中，存在着大量的多目标优化问题。自20世纪70年代以来，关于多目标优化理论与方法的研究已有大量重要而基础的研究成果[1-3]。又由于真实世界中多目标优化问题的数据通常是不确定的，因此研究不确定型鲁棒多目标优化问题就有了十分重要的理论意义与应用价值，其中鲁棒多目标优化问题的最优性条件和对偶性也受到了研究者们的广泛关注。

2013年，Chuong等人[4]考虑了非光滑半无限多目标优化问题，提出了一类根据局部 Lipschitz 函数极限次微分的广义凸和严格广义凸函数，研究了在广义凸和严格广义凸下有效解和弱有效解的充分条件，并且探索了在广义凸和严格广义凸下的弱对偶性和强对偶性；2016年，Chuong[5]考虑不确定鲁棒多目标优化问题，基于Ehrgott等人提出的鲁棒有效解。在广义凸性下，建立了局部鲁棒Pareto有效解和局部鲁Pareto弱有效解的一些最优性条件，表述了鲁棒多目标优化问题的对偶问题，探索广义凸性下的弱对偶性和强对偶性。

受文献[4-5]研究工作的启示，利用极限法锥和极限次微分，进一步在广义伪凸和严格广义伪凸的条件之下研究了一类鲁棒有效解的一些最优性条件和强弱对偶性。

1 预备知识

为了得到结论，首先给出一些基本记号和基本定义。序关系在多目标优化问题研究中扮演了十分基础且重要的作用[6]，一般采用下面空间中序关系：

Rp空间的一些常用子集定义：

的正象限。

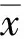
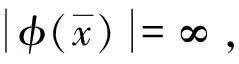
设Rni是欧氏空间且Ωi是Rni的非空紧子集，其中∀i∈(1，...，l)，ni∈N：={1，2，...，q}。

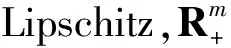
考虑以下形式的多目标优化问题

(UP)minf(x)

s.t.gi(x，wi)≤0，i=1，...，l，

其中x∈Rn是决策变量，wi∈Ωi是不确定参数，gi：Rn×Ωi→R，i=1，...，l是给定的函数。

对于研究的问题(UP)，通常有与之相关的鲁棒对应

(RP)minf(x)

s.t.x∈C，

其中可行集C定义为

C：={x∈Rn|gi(x，wi)≤0，∀wi∈Ωi，i=1，...，l}

(1)

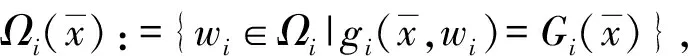
(2)

将问题(UP)的局部鲁棒Pareto(弱)有效解解集定义为locS(RP)(locSw(RP))。

定义中，若U=Rn，则问题(UP)的鲁棒Pareto(弱)有效解解集定义为S(RP)(Sw(RP))。

使得

(3)

2 主要结果

2.1 鲁棒多目标问题的最优性条件

为了刻画问题(UP)的鲁棒Pareto(弱)有效解的充分条件，需要首先给出(f，g)在某一给定点处广义伪凸和严格广义伪凸的定义如下。

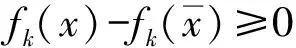
使得

(4)

(5)

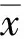
因此

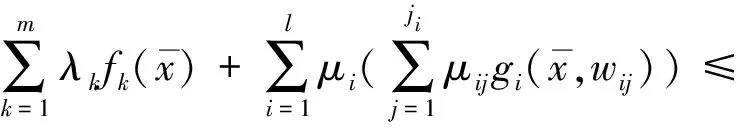
(6)

这必然能够推出存在k0∈{1，...，m}，使得

(7)

(8)

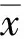
因此

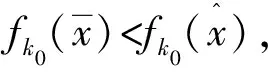
2.2 鲁棒对偶问题的最优性条件

这一部分，首先给出定义并建立鲁棒多目标优化问题的对偶问题，再在广义伪凸和严格广义伪凸的条件之下探索强弱对偶性。

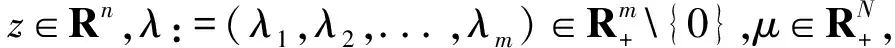
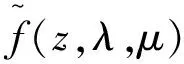
与鲁棒多目标优化问题(RP)相关，下面是对偶鲁棒多目标优化问题

s.t.(z，λ.μ)∈CD

对偶问题(RD)的(局部)鲁棒(弱)有效解的定义类似于定义2，将对偶问题(RD)的鲁棒Pareto(弱)有效解解集记作(Sw(RD))S(RD)。

定理2 (弱鲁棒对偶性)令x∈C和(z，λ，μ)∈CD。

(Ⅰ)若(f，g)在z处是广义伪凸的，则

(Ⅱ)若(f，g)在z处是严格广义伪凸的，则

(9)

(10)

因x∈C，由式(10)可以得到

与式(9)矛盾故(Ⅰ)得证。

再证明(Ⅱ)。反证：假设

(11)

(12)

式(11)意味着x≠z,若x=z，则

由式(11)推出

这是不可能的。因为x∈C可以推出

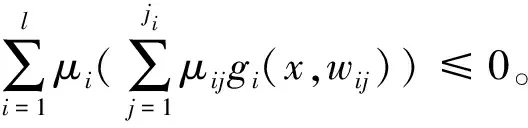
因为x∈C因而可以得到

与式(12)矛盾。故(Ⅱ)得证。

定理3 (强鲁棒对偶性)

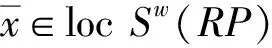
(13)

(14)

故

(Ⅱ)中(f，g)在任意点z∈Rn处是严格广义伪凸的，由定理2的(Ⅱ)则有