安徽省无为第三中学城北校区(238300) 朱小扣

对数是高中数学的重要内容和考点,在研究函数和不等式中具有重要的应用.在高中数学竞赛中的考查频率也颇高,且命题灵活,综合度较高,因而具有一定的难度和挑战性.但随着高考及模拟题不断创新,使得多数人对对数解题的创新运用仍不是很了解,掌握起来也不熟练.为此,本文将通过剖析高考及模拟题中对数的创新应用,进一步探究对数解题应用的新视角.

1.在求导中的运用

例1 (2003年安徽省高考改编)已知m,n是正整数,且1＜m＜n,求证：(1+m)n＞(1+n)m.

证明原命题等价于令则只需证明f(x)在[2,+∞)单调递减即可.两边同时取对数得：两边同时对x求导得：

当x≥2 时,故此时y′＜0 恒成立,即证得.

例2 设

解两边同时取对数得：

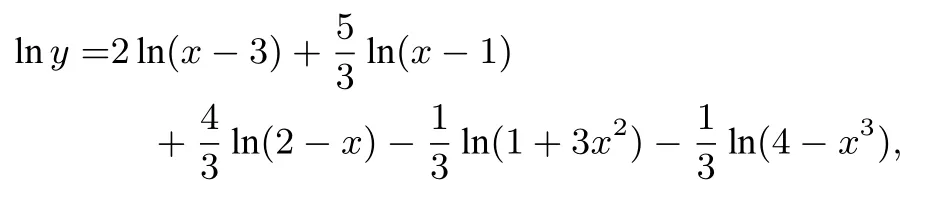
两边同时对x求导得：

点评利用取对数后再求导,有利于将繁琐的问题简化,像例1 等.与此同时,由于是复合函数的求导,故不能用错.

2.在非线性规划题中的运用

例3 已知x,y实数,满足：3 ≤xy2≤8,4 ≤≤9,求的最大值.

解有题设知x,y ∈R+,对原条件两边取对数得：lg 3 ≤ lgx+2 lgy≤ lg 8,lg 4 ≤ 2 lgx-lgy≤ lg 9,令a=lgx,b=lgy,z=则问题转化为：在条件下,求目标函数z=3a-4b的最大值.画出可行域,易得zmax=lg 27,故

例4 已知动点P(x,y)满足：则x2+y2-2x的最小值为____.

解析xy≤yx ⇔lnxy≤lnyx ⇒ylnx≤xlny ⇒令则f′(x)=恒成立.则f(x)在(0,2]上单调递增,故y≥x.问题转化为在条件下,求x2+y2-2x的最小值.

设P(x,y),Q(1,0),则x2+y2-2x=PQ2-1,如图1易知：PQ≥MQ,故x2+y2-2x=PQ2-1 ≥MQ2-1=故答案为

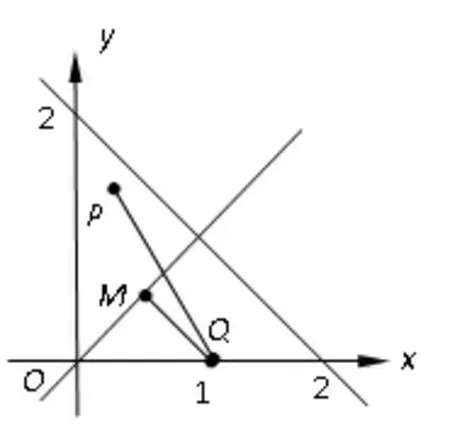
图1

点评这类题能考察学生对线性规划的掌握情况,通过取对数可以将非线性条件转化线性条件,进而用线性规划的方法求最值,这能极大拓宽了线性规划的应用范围.

3.在求通项公式中的运用

例5 数列{an}满足a1=1,an+1=求{an}的通项公式.

解对原式两边同时取倒数得：

例6 (2016年内蒙古省预赛题)数列{an}满足求{an}的通项公式.

解对原式两边同时取倒数得：

点评利用取对数方法,可以将不是齐次的数列递推公式,转化为齐次的递推公式,进而可以转化为等差或等比数列,使得问题能顺利解出.

4.在琴生不等式中的运用

例7 设ai＞0,i=1,2,3,··· ,n.证明：

证明令f(x)=lnx(x＞0),则f′′(x)恒成立,所以f(x)在(0,+∞)是上凸函数,故

综上可得：

例8 (08年南京大学自招)设a,b,c ∈R+且a+b+c=1,求证：

证明令f(x)=则

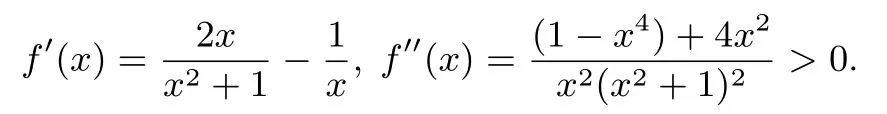
由琴生不等式得：

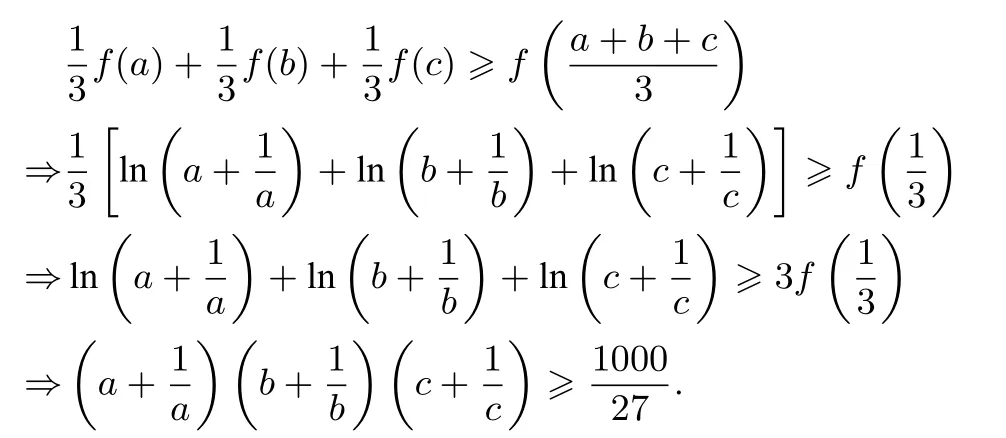
例9 在△ABC中,α,β,γ ∈R+,求证：

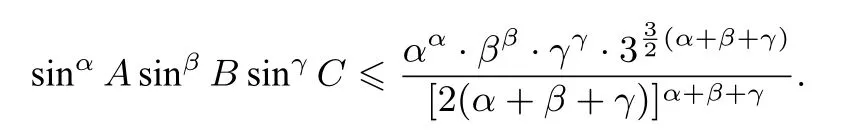
证明令f(x)=lnx,x ∈(0,1),则由琴生不等式得：

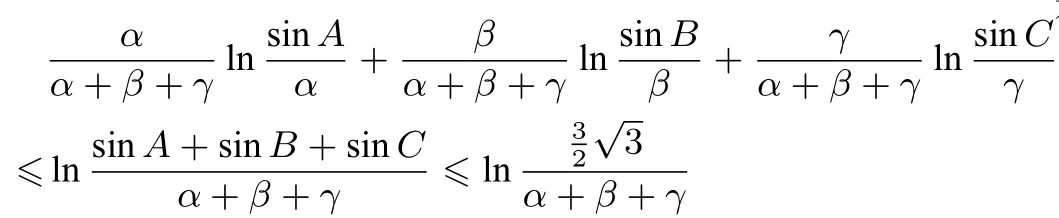
(我们知道：sinA+sinB+sinC因此,

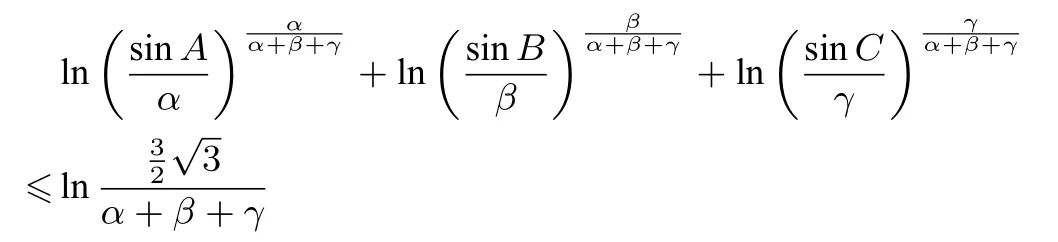
因此,sinα Asinβ Bsinγ

点评运用对数法辅助琴生不等式去证明问题,化归得当是难点,合理构造函数是重点,拼凑是关键.若能把握住重难点和关键就会运用自如,并可以解决很多高考和竞赛题.

5.对数平均不等式在解题中的运用

引理对数平均不等式：(b＞a＞0).

例10 (2017年苏州市届高三调研)已知函数f(x)=(lnx-k-1)x(k ∈R).

(1)当x＞1 时,求函数f(x)的单调区间和极值;

(2)若对于任意x ∈[e,e2],都有f(x)＜4 lnx成立,求实数k的取值范围;

(3)若x12,且f(x1)=f(x2),证明：x1x2＜e2k.

解(1),(2)略; (3)不妨设x1＞x2,由f(x1)=f(x2)得：(lnx1-k-1)x1=(lnx2-k-1)x2,解 得：k=欲证：x1x2＜e2k,即证lnx1+lnx2＜2k ⇔lnx1+lnx2＜由对数平均不等式可知上述不等式成立,即证得.

例11 (2016年湖南预赛)已知函数f(x)=xlnx-

(1)当m=-2 时,求函数f(x)的所有零点;

(2)若f(x)有两个极值点x1,x2,且x1＜x2,求证x1x2＞e2.

解(1)当m=-2 时,f(x)=xlnx+x2-x=x(lnx+x-1),x＞0.设p(x)=lnx+x-1,x＞0,则p′(x)=+1＞0,于是p(x)在(0,+∞)上为增函数.又p(1)=0,所以,当m=-2 时,函数f(x)有唯一的零点1.

(2)若f(x)有两个极值点x1,x2,则导函数f′(x)有两个零点x1,x2.由f′(x)=lnx-mx,可知要证x1x2＞e2,即证明lnx1+lnx2＞2.由得所以即故只需证因为x1＜x2,故只需证由对数平均不等式可知上述不等式成立,综上知,x1x2＞e2得证.

点评用对数平均不等式能解决很多诸如极值点偏移的问题,在此不一一例举,但在每次解答时必须要将对数平均不等式的证明过程写出,不然会导致扣分.

总结以上列举了运用对数思想解五类高考题,在解决类似的问题时,应多角度,多思维的去考虑.与此同时,方法和技巧也不能生搬硬套,必须自己尝试、自己领悟,这样才能在解题中达到自身水平的提高.这样才能一题多解,才能一解多题! 希望此文带来新的视角让大家对对数法解题有更深的认识,达到用对数法解题能力的提升.