湖南省衡南县第一中学(421141) 谢德斌

纵观全国各地历年高考导数题,以对数平均不等式及变式为背景的导数压轴题不在少数,学生在解决此类问题时,往往未能真正把握试题背景与思路,心存畏惧心理,要么因动不了笔,直接放弃;要么乱写一气,切不中要害,导致这类题型得分率很低.本文摘取了近年来各地高考真题,深入分析了导数综合大题的共性特点及解决方法,期望能对读者有所启迪和感悟.

一、问题的提出

现有反比例函数f(x)=(x＞0)的图象,如图(1)(2)所示,作AP//BQ//V K//UT,设(其中b＞a＞0),f(x)在点K处的切线分别与AP,BQ交于E,F,过点K的直线MN//x轴且分别与AP,BQ交于M,N.试探究如下问题：

(1)如图1,由曲边梯形ABQP与梯形ABFE面积大小的关系提炼相应的不等式;

(2)如图2,由曲边梯形AUTP与梯形AUTP面积的大小关系提炼相应的不等式;

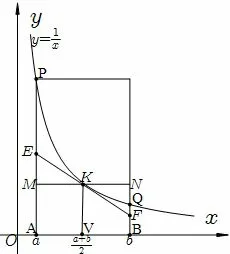
图1

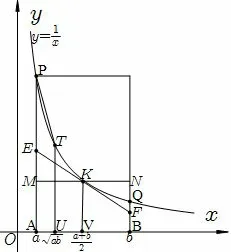
图2

分析(1)由S曲边梯形ABQP＞S梯形ABF E=S矩形ABNM,即所以

(2)由S曲边梯形AUT P＜S梯形AUT P,即即所以

由(1)(2)及基本不等式可得到一个不等式链：a＜(其中0＜a＜b).

二、从对数平均不等式的代数证明方法追根朔源

分析1 由于a,b是两个独立的变量,如果能够变形为一个整体,则可通过换元再构造函数利用单调性得证.观察到两边成齐次结构式形状,故可先做如下变形：令即证由则g(t)在t ∈(1,+∞)上单调递增,所以g(t)＞g(1)=0.

分析2 要证的不等式含两个独立变量,不防将其中一个视为主元,另一个视为常量来处理.(a+b)(lnb-lna)-2(b-a)＞0.令g(x)=(a+x)(lnxlna)-2(x-a)(x＞a),原问题转化为证明：g(b)＞0 即可.由g′(x)=(lnx-lna)+-2=lnx-lna+-1,则g′(x)在x ∈(a,+∞)上单调递增,所以g′(x)＞g′(a)=0,则g(x)在x ∈(a,+∞)上单调递增,由0＜a＜b,所以g(b)＞g(a)=0.

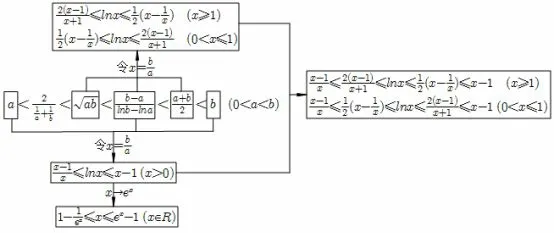
对数平均不等式衍生不等式关系图

三、由对数平均不等式衍生的其它基本函数不等式及网络关系图

事实上,由对数平均不等式链,通过齐次化变形后再换元,可得到如上图所示的常见基本函数不等式.

四、对数平均不等式链及变式在高考导数题中的运用

(一)对数平均不等式链及变式在“证明不等式”中的运用

例1 (2018年新课标卷I 理科)已知函数f(x)=

(1)讨论f(x)的单调性;

(2)若f(x)存 在 两 个 极 值 点x1,x2,证 明：

分析1 (1)略.

(2)f′(x)=由(1)知,当且仅当a＞2时,f(x)存在两个极值点x1,x2,且x1,x2满足x1x2=1,不妨设x1＜x2,又x1,x2∈(0,+∞),则x2＞1.因为

转化至此,可看出以对数平均不等式为背景显然易见,运用对数平均不等式可知,成立.

分析2 事实上,本题由于x1x2=1,故也可消元后构造函数,利用单调性证明.

练习1 (2005年湖南卷)已知函数f(x)=lnx,设函数f(x)的图象C1与函数g(x)的图象C2交于点P.Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M.N,证明：C1在点M处的切线与C2在点N处的切线不平行.

分析设P(x1,y1),Q(x2,y2),(x1,x2∈(0,+∞),x12).由则有：

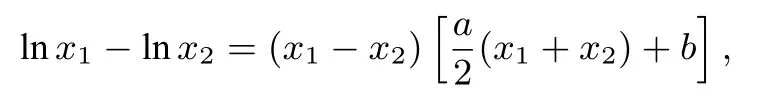
即

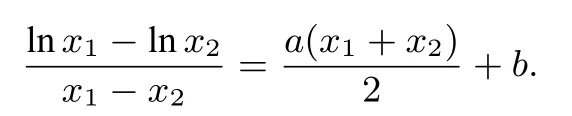
因为C1在M处的切线斜率

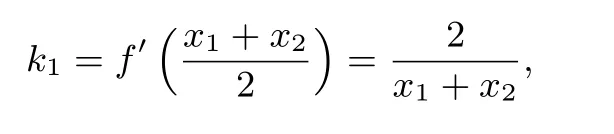
C2在N处的切线斜率

原问题转化为即证：k12,由对数平均不等式知：故k12.

练习2 (2010年高考天津卷)已知函数f(x)=xe-x(x ∈R),如果x12,且f(x1)=f(x2).证明：x1+x2＞2.

分析由f′(x)=(1-x)e-x,则f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减,且当x＞0 时,f(x)＞0,因为f(x1)=f(x2),不妨设x1＜x2,则有0＜x1＜1＜x2,由x1e-x1=x2e-x2,则 有lnx1-x1=lnx2-x2,即由对数平均不等式知故x1+x2＞2.

评注对这类典型的“极值点偏移”问题的处理,构造辅助函数利用单调性证明也不失为较好的方法,本题中：等价转化为0＜2-x2＜x1＜1,构造g(x)=f(2-x)-f(x)(x＞1)只须证明g(x)在x ∈(0,1)上单调递减即可.

例2 (2018年新课标卷I 文科)已知函数f(x)=aex-lnx-1,证明：当a≥时,f(x)≥0.

分析要证的式子中既含有ex,又含有lnx结构式,可尝试考虑ex,lnx的不等式链实现放缩.由前述第三部分中的网络关系图中可知,由或换元及变形后可得如下两个基本函数不等式链：①2○ex≥x+1(x ∈R).本题中：要证f(x)≥0,转化为即证：当a≥时,a·ex≥lnx+1,由基本函数不等式链知：a·ex≥ex-1≥x≥lnx+1,得证.

练习3 (2013年新课标卷II)已知函数f(x)=ex-ln(x+m).当m≤2 时,证明：f(x)＞0.

分析由基本函数不等式链知：当m≤2 时,ln(x+m)≤ln(x+2)≤x+1 ≤ex,而ln(x+2)=x+1 当且仅当x=-1,x+1=ex当且仅当x=0,所以等号同时取不到,故当m≤2 时,f(x)＞0.

(二)对数平均不等式链及变式在“含参不等式恒成立求参数范围问题”中的运用

例3 (2017年新课标卷III)已知函数f(x)=x-1-alnx.

(1)若f(x)≥0,求a的值;

(2)设m为整数,且对于任意正整数n,求m的最小值.

分析对这类题型通常的处理方法：一是直接求导分类讨论; 二是分离参数.由f(x)结构式特征：想到lnx≤x-1(x＞0)这一利器的运用,可尝试分离参数处理.

(1)f(x)≥0⇔x-1 ≥alnx.

①当x=1 时,a ∈R;

②当x＞1 时,a≤恒成立,由平均不等式链变式可知：lnx＜x-1(x＞1),即此时则a≤1;

③当0＜x＜1 时,a≥恒成立,由基本函数不等式可知：lnx＜x-1(0＜x＜1),即此时则a≥1.

综合 ① ② ③得,a=1.

(2)通过两边取对数,将左边积变和式,通过适当放缩使之和可求出.由对数平均不等链变式有：lnx≤x-1(x＞0),则ln(x+1)≤x(x＞-1)取x=即有ln所以故m的最小值为3.

练习4 (2011年新课标卷)已知函数f(x)曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.如果当x＞0,且1 时,求k的取值范围.

分析易得a=b=1,由f(x)＞即1-k＞由对数平均不等式：或换元及变形后可得如下基本函数不等式：所以当x＞0 且1时,有故1-k≥1,即k≤0.

(三)对数平均不等式链及变式在“函数零点及恒成立问题取点”中的运用

例4 (2017年新课标卷I)已知函数f(x)=ae2x+(a-2)ex-x.若f(x)有两个零点,求a的取值范围.

分析含参函数零点问题的处理思路一般有如下两种：一是直接分类讨论单调性结合零点存在性定理求解; 二是分离参数运用函数方程思想解决.为使方法具有通用性,我们不妨按思路一来解决此题.由f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1)(x ∈R)

①若a≤0,则f(x)在(-∞,+∞)上单调递减,f(x)至多有一个零点.

② 若a＞0,则f(x)在(-lna,+∞)上单调递增,在(-∞,-lna)上单调递减,则fmin(x)=f(-lna)=当a=1 时,f(-lna)=0,此时f(x)只有一个零点;当a＞1 时,fmin(x)=f(-lna)＞0,此时f(x)没有零点;当0＜a＜1 时,fmin(x)=f(-lna)＜0,而f(-1)=所以f(x)在(-1,-lna)上有一个零点,下证f(x)在(-lna,+∞)上有一个零点即可.即证∃x0＞-lna,使f(x0)＞0 即可,根椐零点存在性定理,即说明了f(x)在(-lna,x0)上有一个零点.由对数平均不等式链及变式则有：ex≥x+1＞x,则-x＞-ex,由f(x)＞ae2x+(a-2)ex-ex=ex(aex+a-3)可得这样一来,就找到了使得f(x0)＞0,所以f(x)在上存在一个零点,

综上：当0＜a＜1 时,f(x)有两个零点.

评注本题的难点在于找点,当0＜a＜1 时,说清∃x0,使f(x0)＞0.解决此类找点问题时,我们不妨联想到对数平均不等式链及变式将超越不等式某些项放缩,变成常规的一次或二次不等式来找点.

练习5 (2010年全国新课标卷)设函数f(x)=ex-1-x-ax2,若当x≥0 时f(x)≥0,求a的取值范围

分析f′(x)=ex-1-2ax,观察到f(0)=0,先求f(x)≥0 的一个充分条件.由f′(x)=ex-1-2ax≥x-2ax=(1-2a)x,当时,f′(x)≥0,此时f(x)在[0,+∞)上单调递增,则有f(x)≥f(0)=0;再验证必要性,即证明∃x0＞0,当x ∈(0,x0)时,f(x)＜0 即可.当时,由ex≥x+1,则-x≤e-x-1,由f′(x)=ex-1-2ax≤可得x＜ln(2a),这样一来就找到了x0=ln(2a),当x ∈(0,ln(2a))时,f′(x)＜0,从而可得f(x)＜f(0)=0,与题意相矛盾.综上：a≤即为所求.

站在系统的高度来研究这类导数综合题的通性通法及背景,引导学生理清知识脉络,对我们的复习备考效率的提高无疑会有很大的推动作用.