井沛良， 段宇， 韩超， 郭荣化， 宁小磊， 刘瑜

(1.中国华阴兵器试验中心， 陕西 华阴 714200； 2.空军军医大学， 陕西 西安 714299； 3.海军航空大学， 山东 烟台 264001)

0 引言

作为评估无控炮弹、有控导弹等攻击类武器打击精度和雷达、光电等侦察类装备目标定位精度的重要评估指标之一，圆概率误差(CEP)在国内外武器装备实验与评估中得到广泛应用[1-3]。与命中概率[4-5]、命中/定位准确度[6](偏差)以及命中/定位密集度[7-8](方差)等评估指标无需假设攻击点/定位点概率分布模型不同，现有CEP计算方法高度依赖于攻击点/定位点概率分布模型。由于大部分武器装备的攻击点/定位点都呈现出单一密集中心特性，可以认为其分布服从或近似服从高斯分布。同时，高斯分布可由其1阶原点矩和2阶中心矩完全表述，而1阶原点矩和2阶中心矩可通过矩估计方法由样本数据计算得到，故目前可查文献中CEP计算方法大都采用了高斯分布模型。然而在实际实验中，攻击点/定位点时常会呈现出多密集中心现象，此时采用高斯分布模型显然不再适合。国家军用标准GJB 6289—2008和GB/T 4882—2001指出，利用高斯分布模型进行CEP计算前需进行正态性检验，只有通过正态性检验的实验数据才可以使用高斯分布模型进行CEP计算。而对于未通过正态性检验的实验数据，如呈现多密集中心的实验数据，目前尚无计算CEP的具体标准可以依据。

针对上述问题，本文拟采用高斯混合模型(GMM)[9-10]作为攻击点/定位点通用概率分布模型，并使用期望最大化(EM)算法[11]迭代求解模型参数，进而使用二分法计算CEP指标。采用该处理思路原因有3个方面：1)GMM作为非线性贝叶斯滤波[12-13]的关键实现模型之一，使用多个不同高斯概率密度函数(PDF)的加权和近似描述任意PDF，可在参与加权高斯PDF数量足够多的条件下，使得近似误差收敛于0，因此特别适合于描述多密集点特性的攻击点/定位点概率分布；2)GMM待估计参数个数随着参与加权高斯PDF数量的增加呈线性增加，因此即使采用最简单的最大化似然(ML)参数估计方法[14-15]或传统网格搜索法，计算量也十分巨大。虽然也可以尝试使用蚁群算法[16-17]、遗传算法[18-19]、模拟退火算法[20-21]等现代优化算法，但是考虑到目前EM算法求解GMM参数在工程中应用更为广泛，故本文采用EM算法进行GMM参数的ML估计计算；3)GMM为其参数的指数和函数形式，其在圆域上的积分往往需转换至极坐标系下进行，因此给定GMM参数和圆域积分概率求解CEP的解析表达式十分困难，基于此，本文拟在给定最大积分概率误差约束条件下，采用二分法求解CEP.

1 GMM和EM算法

1.1 GMM

GMM基本思想为使用一组高斯分布PDF加权和来近似描述任意PDF，即

(1)

式中：x为观测矢量；K为高斯分量总个数，wk为第k个高斯分量的权重系数；N(x;μk,Rk)为第k个高斯分量的PDF，且

(2)

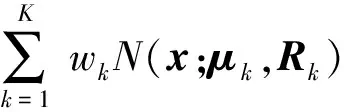
1.2 EM算法

EM算法广泛应用于ML估计的多参数求解问题。ML估计作为经典估计理论的重要方法之一，由于其求解思想简单、渐近有效，在很多工程问题中得到广泛应用。ML估计参数的典型求解方法有很多，如：1)最直接的方法是对似然函数关于各个待求参数求解导数，进而求解微分方程或方程组。但该方法往往与似然函数的函数形式有很大关系，经常因为函数形式复杂而难以求得解析解；2)网格搜索法[22]求解逻辑简单，但计算复杂度随参数数量增多呈指数增加；3)Newton-Raphson迭代法[23-24]可能会遇到收敛问题。当然还可以使用遗传算法、蚁群算法和模拟退火算法等现代优化算法求解ML参数估计问题，但由于EM算法在求解GMM参数时，收敛速度快且可以保证收敛，本文采用EM算法对GMM的ML参数进行计算。

假设观测数据为{x1,x2,…,xM}，数据间相互独立，待估计参数为矢量θ，则似然函数可以写成(3)式形式：

(3)

由于对数函数不改变函数的单调性，因此ML函数可通过最大化对数似然函数

(4)

求得。EM算法的关键是引入隐含变量的概念来对估计问题进行分解，隐含变量的引入应使得估计问题变得简单易行，设隐含变量为z(m)，则(4)式可写为

(5)

式中：Qm(z(m))为隐含变量的PDF. (5)式的推导使用了Jensen不等式[25]。由Jensen不等式性质可知，无论m取任意值，f(xm,z(m);θ)/Qm(z(m))都为固定常数时，(5)式中等号成立。又由于

(6)

从而可得

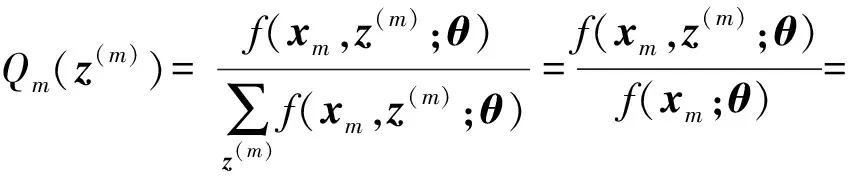
(7)

(7)式即为EM算法的E步，而EM算法的M步则是基于(7)式所得Qm(z(m))对估计问题进行分解，进而采用一般ML求解方法计算：

(8)

从(8)式可以发现，E步中计算Qm(z(m))需要事先已知θ，而M步中计算θmax需要事先已知Qm(z(m)). 因此，EM算法具体操作时往往采取迭代计算方法，即事先给定参数初始值θ0，然后代入(7)式得到Qm(z(m))，再把Qm(z(m))代入(8)式得到θmax，如此交替使用(7)式和(8)式进行迭代，直至相邻两次迭代得到的θmax基本不变时结束迭代，并把迭代结果作为最终θ估计值。

2 非高斯分布CEP求解具体步骤

2.1 观测数据收集和整理

观测数据是指攻击类/侦察类装备在指定坐标系下的命中/定位坐标值，通常可写成矢量x的形式。坐标系一般选择笛卡尔直角坐标系，坐标原点选在靶标或待侦察目标中心点。

2.2 GMM参数选择

GMM选用(1)式所示形式。确定高斯分量总个数K是采用GMM的关键。理论上，可以使用分量尽可能多的GMM. 在求解出模型参数后，仅选取权重较大的高斯分量来重构PDF，舍弃那些权重较小的，这种方法尤其适合人不在回路时大数据的自动处理。对于武器装备CEP评估，由于人往往都在回路中，高斯分量个数可以选择目视密集中心个数。

2.3 EM算法实施步骤

使用EM算法求解GMM参数的具体计算实施步骤如下。

步骤1给定参数初始值。

取初始权重参数为

wk=1/K.

(9)

步骤2约定隐含变量及内涵。

对于GMM来讲，由模型生成观测数据的物理内涵可以理解为：依据权重参数wk来随机选取高斯分量，然后依据所选取分量的PDF(即N(x;μk,Rk))来生成具体观测。因此，隐含变量z(m)可以构建为观测矢量xm与高斯分量的隶属关系，即xm到底由哪个高斯分量生成这一随机事件，而Qm(z(m))则表述了xm隶属于第z(m)个高斯分量的概率。

步骤3依据当前参数模型，求解出Qm(z(m)).

(10)

步骤4依据E步所得Qm(z(m))，对GMM参数进行更新。

(11)

(12)

(13)

步骤5重复步骤3和步骤4，直到相邻两次所得GMM参数基本不变。

2.4 针对GMM的二分法CEP计算方法

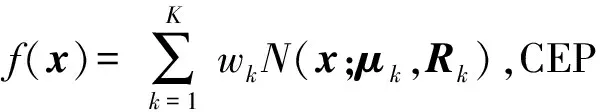
(14)

式中：|·|为矢量2范数操作。显然，直接求解出CEP是困难的，因为给定f(x)在|x|≤r约束区域的积分概率，很难写出以r为自变量的解析表达式。然而，考虑到给定的r取任意值时，f(x)在|x|≤r约束区域的积分概率容易求解出，且p(r)为r的单调不减函数的现实，可以在给定p(r)精度ξ(后续仿真实验中ξ取为1×10-6)要求的前提下，使用二分法迭代求解r，其基本步骤如下。

步骤1初始化。

步骤2二分法求解结果测试。

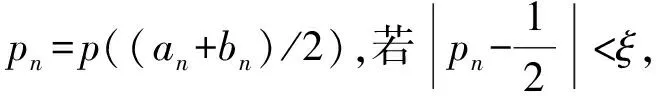
步骤3二分法收缩可行解区间。

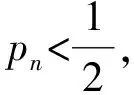
[an+1,bn+1]=[(an+bn)/2,bn]；

(15)

否则取

[an+1,bn+1]=[an,(an+bn)/2]；

(16)

并令n=n+1.

步骤4如果n=N，则取CEP=(an+bn)/2，并结束迭代；否则跳转至步骤2.

3 仿真结果与分析

3.1 算法单次实施典型仿真结果与分析

以一个简单的二分量GMM为实施例进行仿真。模型真实参数设置如下：K=2，w1=2/5，w2=3/5，μ1=[2,2]T，μ2=[4,5]T，R1=diag([1,1]T)，R2=diag([1,2]T)；EM算法初始GMM参数设置为：K=3，w1=1/3，w2=1/3，w3=1/3，μ1=[1,1]T，μ2=[5,6]T，μ3=[7/2,7/2]T，R1=diag([3,4]T)，R2=diag([2,3]T)，R3=diag([3,3]T). 可得真实PDF曲面和EM算法初始GMM的PDF曲面分别如图1和图2所示。

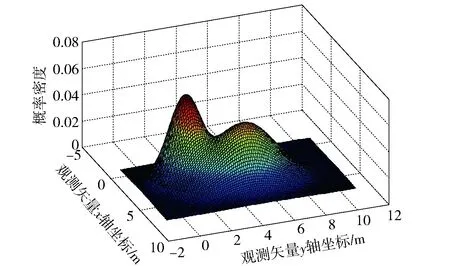
图1 真实PDF曲面Fig.1 Surface of true PDF

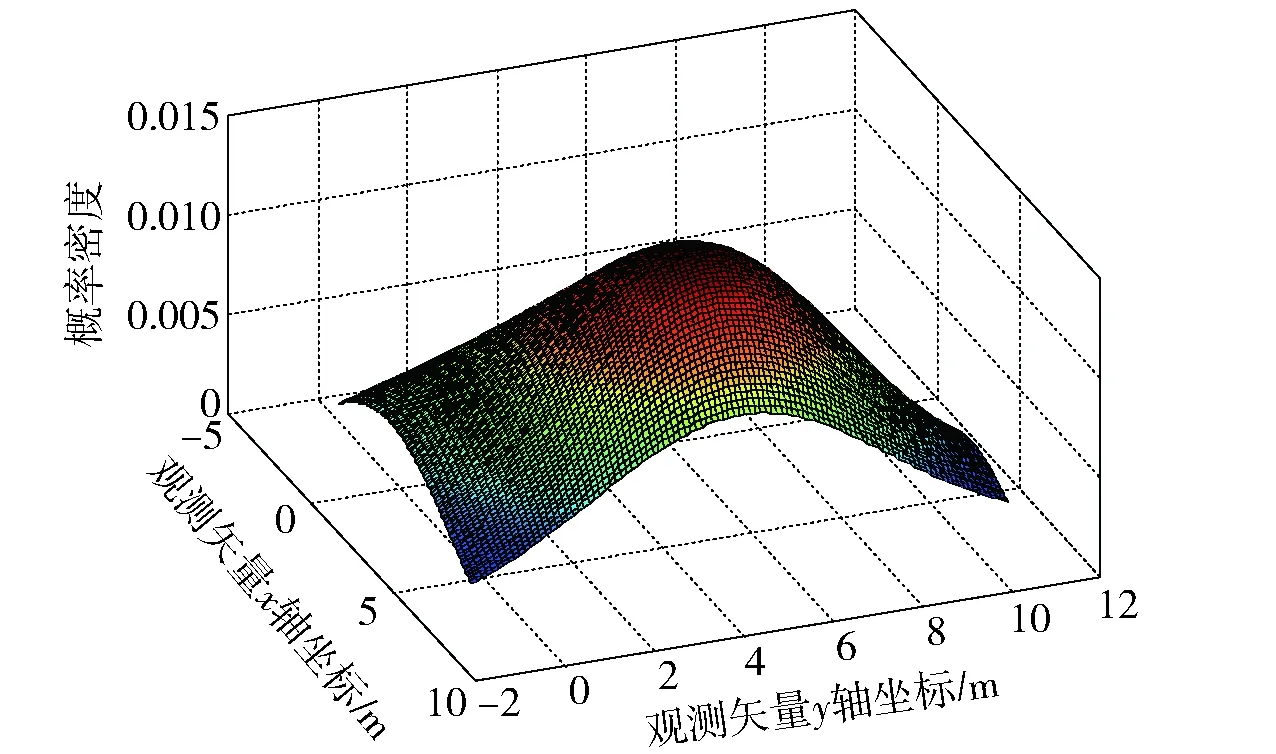
图2 EM算法初始设置GMM的 PDF曲面Fig.2 Surface of initial GMM PDF derived by EM algorithm

依据真实PDF生成200个观测数据，如图3所示。针对生成观测数据，EM算法最终迭代求解出GMM的PDF曲面如图4所示。

图3 依据真实PDF生成观测Fig.3 Observations generated by true PDF

图4 EM算法最终迭代求解出GMM的 PDF曲面Fig.4 Surface of GMM PDF derived by EM algorithm

图4所表征的GMM中高斯分量的权重、均值、协方差阵依次为：w1=0.341 8，w2=0.351 3，w3=0.304 9，μ1=[1.867 3,1.675 5]T，μ2=[4.189 5,5.711 2]T，μ3=[3.399 7,3.436 8]T，R1=diag([1.018 8,0.881 0]T)，R2=diag([0.935 1,1.903 7]T)，R3=diag([1.144 0,1.640 5]T). 把图4、图2分别与图1进行对比可以发现，EM算法迭代求解GMM的PDF曲面较初始设置GMM的 PDF曲面明显更接近于真实PDF曲面。另外，将EM算法迭代前后GMM中高斯分量的均值和协方差阵分别与真实GMM中高斯分量的均值和协方差阵进行对比可以发现，EM算法迭代使得GMM前两个高斯分量更接近于真实GMM的两个高斯分量，这表明了EM算法的良好性能。

为了定量对比本文算法和传统单高斯模型的性能优劣，采用经典Kullback-Leibler(KL)区分度[26]指标以及PDF差值绝对值积分指标对算法性能，即算法求解PDF与真实PDF的相似度，进行评价。KL区分度是衡量两个PDF差异大小的经典指标，KL区分度越小，表明两个PDF越趋于相同。为了更好地展示不同算法性能细节，本文后续部分采用了KL区分度的对数值来表征不同函数之间的接近程度。对于给定的两个PDF：f1(x)和f2(x)，f2(x)相对于f1(x)的KL区分度定义如下：

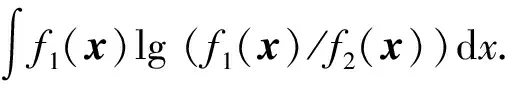
(17)

由于lg(·)为上凸函数，由Jensen不等式可知，dKL(f1(x)‖f2(x))≥0总是成立，且等号成立时有f1(x)=f2(x). 与KL区分度类似，PDF差值绝对值积分指标也可以对两个PDF接近程度进行评价，PDF的f2(x)相对于f1(x)的差值绝对值积分定义如下：

(18)

显然，两个PDF越相似，其差值绝对值积分越小。当差值绝对值积分为0时，两个PDF完全一致。

定义真实PDF为fT，隐含变量已知时PDF为fH，传统方法求解PDF为fRSGM，初始GMM的PDF为fIGMM，EM算法迭代求解GMM的PDF为fRGMM，可得fRSGM、fIGMM、fRGMM分别与fT、fH这两个参考基准之间的KL区分度如图5所示，差值绝对值积分如图6所示。

图5 不同PDF之间对数KL区分度Fig.5 Logarithmic KL divergence between different PDFs

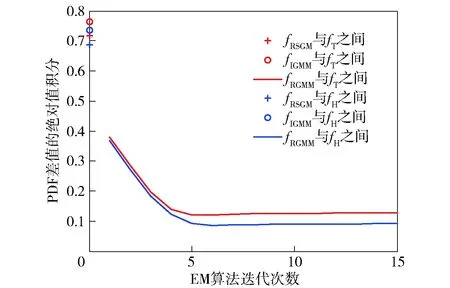
图6 不同PDF之间差值绝对值积分Fig.6 Integral of absolute value of difference between different PDFs

注意：fRSGM、fIGMM、fT、fH并不随着EM算法的迭代而发生变化，因此fRSGM、fIGMM与fT、fH之间的指标值仅在图5、图6中的第0次迭代位置处给出。而fRSGM与fT、fH之间的指标值为EM算法迭代次数的函数，因而以曲线形式展示。从图5和图6中可以看出，采用EM算法求解GMM参数，能够快速、稳定地收敛到一个显著优于单高斯模型参数的结果值。由于EM算法需要克服隐含参数来求解GMM参数，因此相对于fT，EM算法迭代结果更趋近于fH. 这恰恰表明了EM算法的优异性能，当观测矢量个数足够多时，fT与fH足够相似，此时EM算法便通过逼近fH来逼近fT.

如图7所示给出了EM算法迭代过程中，初始GMM分量中心位置的收敛变化轨迹。同时，依据求解PDF计算出了不同PDF的CEP圆域，并以圆圈的形式画出。

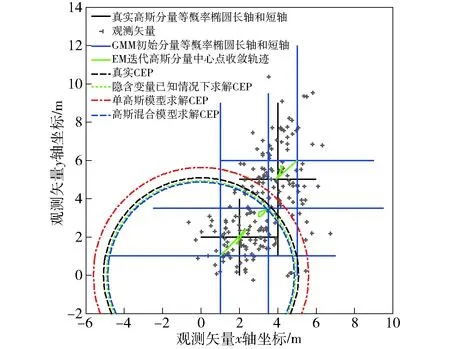
图7 EM算法迭代收敛轨迹及不同算法CEP求解 结果对比示意图Fig.7 Iterative convergence trace of EM algorithm and CEP results of different algorithms

从图7中可以看出，fT与fH求解出的CEP基本一致，而本文方法求解CEP要比传统方法求解CEP更接近真实PDF所对应的CEP.

3.2 算法多次Monte Carlo仿真性能曲面对比与分析

为了更充分对比算法性能，固定3.1节中初始GMM参数设置，并在变化真实GMM中高斯分量中心位置的同时，保持真实GMM中高斯分量协方差阵和高斯分量系数不变。真实GMM中高斯分量中心位置仅作平移变化，对每一平移变化后的真实GMM，采用Monte Carlo方法生成100组观测数据。针对每一组数据分别使用传统方法和本文方法求解出对应PDF及CEP，并计算所得PDF与真实PDF相似程度以及所得CEP与真实CEP的接近程度。对所有对比结果进行统计，即可得到传统方法和本文方法平均性能。当GMM中高斯分量中心位置在一定区域多次进行平移时，便可得到一个平均性能的曲面。这里采用的性能指标有PDF之间的KL区分度(如图8、图9所示)、差值绝对值积分(如图10、图11所示)以及CEP的均方误差(如图12、图13所示)。曲面对应的x轴坐标值和y轴坐标值分别表示GMM中高斯分量中心位置在x轴方向和y轴方向上的平移幅度。

图8 传统方法求解PDF与真实PDF之间对数KL区 分度均值曲面Fig.8 Surface of average logarithmic KL divergence between PDF derived by traditional method and true PDF

图9 本文方法求解PDF与真实PDF之间对数KL区 分度均值曲面Fig.9 Surface of average logarithmic KL divergence between PDF derived by the proposed method and the true PDF

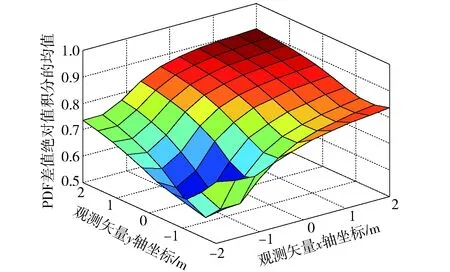
图10 传统方法求解PDF与真实PDF之间差值 绝对值积分的均值曲面Fig.10 Integral mean value of absolute value of difference between PDF derived by traditional method and true PDF

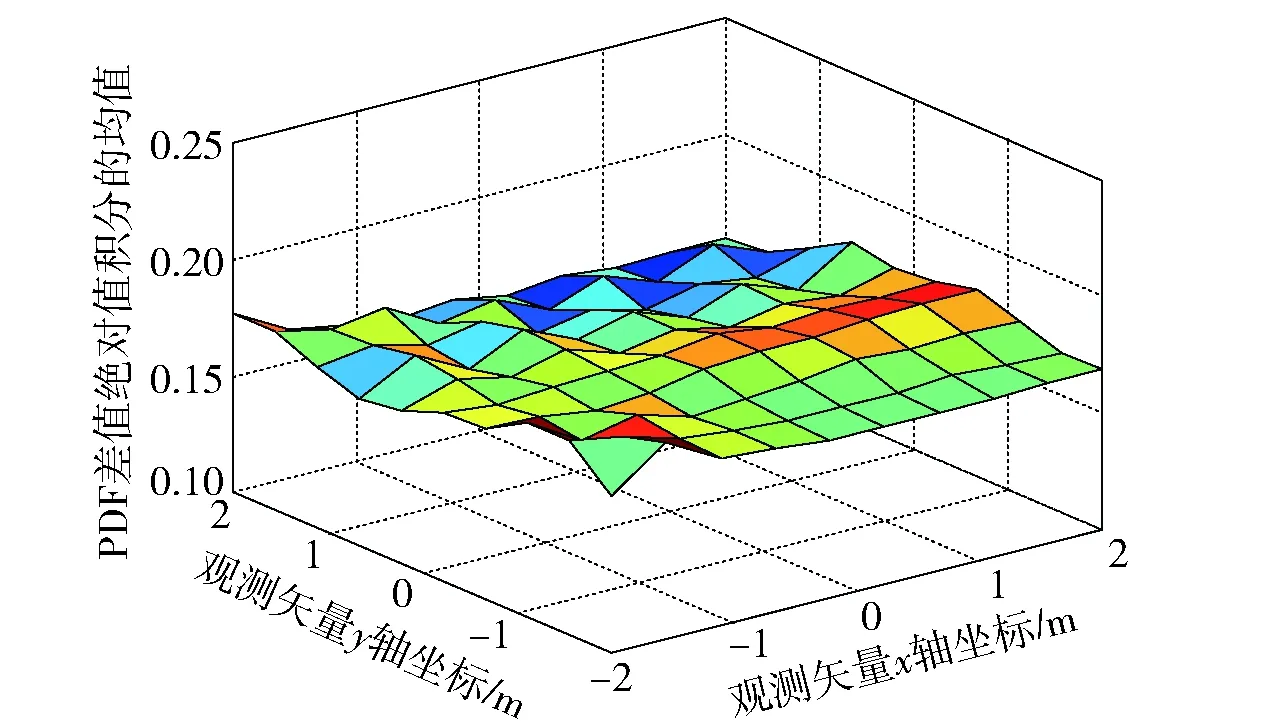
图11 本文方法求解PDF与真实PDF之间差值绝对值 积分的均值曲面Fig.11 Integral mean value of absolute value of difference between PDF derived by the proposed method and true PDF

图12 传统方法求解CEP均方误差曲面Fig.12 Mean square error of CEP derived by the traditional method

图13 本文方法求解CEP均方误差曲面Fig.13 Mean square error of CEP derived by the proposed method

从图8、图9、图10和图11可以看出，本文方法在变化参数的总体范围内，相较于传统方法能够取得更接近于真实PDF的PDF估计。由图12和图13可知，图12曲面积分值为68.376 3，图13曲面积分值为5.311 6，二者对比结果表明，本文方法求解CEP的均方误差显著小于传统方法求解CEP的均方误差。这说明，本文方法相对于传统方法具有十分优异的CEP估计性能，十分适用于观测数据非高斯分布时的CEP估计问题。

4 结论

本文分析了传统CEP求解方法在处理观测数据呈现非高斯分布时存在的缺陷，并基于GMM和EM算法，提出了观测数据服从任意分布时的CEP求解新方法。仿真结果表明，无论从KL区分度，还是从PDF差值绝对值积分来分析，所提方法求解出的PDF相较于传统方法明显能够更接近真实PDF. 最终求解CEP的均方误差结果也揭示了本文方法的优异性能。