两体懒态的几种刻画
2019-02-23侯晋川
刘 亮, 侯晋川
(1. 太原理工大学 力学学院, 山西 太原 030024; 2. 太原理工大学 数学学院, 山西 太原 030024)
0 引 言
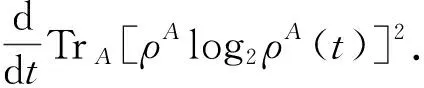
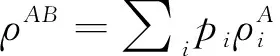
在有限维的情况下, Xu J W[12]给出了一个两体懒态的判据, 并且研究了懒态和纠缠态, 以及懒态和Discordant态的关系. 对于连续系统, Xu J W[13]发现一个高斯态是懒态当且仅当它是热态的张量积. 而在一般无限维情形下, 没有给出判别懒态的方法. 本文给出了没有维数限制的懒态判据, 并且结合新的判据, 讨论了无限维情形下懒态和纠缠态以及Discordant态的关系.
在给出主要结论之前, 先介绍一些预备知识. 假定dimHA⊗HB=∞, |iA〉和|iB〉分别是希尔伯特空间HA和HB上固定的一组正交基. 令Fij=|iB〉〈jB|, 那么, 任意一个S(HA⊗HB)里的两体态ρAB都可以表示为[14]
ρAB=∑ijAij⊗Fij,
式中:Aij为HA上依迹范数收敛的迹类算子. 也就是
且ρA=TrB(ρAB)=∑iAii. 类似的, 任意一个ρAB∈B(HA⊗HB)上的态可以按A系统的一组基展开, 表示为ρAB=∑klEkl⊗Bkl, 其中Bkl为HB上依迹范数收敛的迹类算子.
1 主要结论及证明
定理1 对任意的两体态ρAB=∑ijAij⊗Fij∈B(HA⊗HB),ρAB是懒态当且仅当对所有的(i,j),Aij和约化态ρA交换.
证明假定|iA〉和|iB〉分别是希尔伯特空间HA和HB上一组给定的正交基, 那么ρAB可以表示为ρAB=∑ijAij⊗Fij, 其中Fij=|iB〉〈jB|, 约化态ρA=(I⊗Tr)ρAB=∑iAii. 由定义,ρAB是懒态当且仅当[ρAB,ρA⊗IB]=0, 进而有
∑ijAij⊗Fij·∑iAii⊗I=
∑iAii⊗I·∑ijAij⊗Fij
∑ijAij⊗Fij·(ρA⊗I)=
(ρA⊗I)·∑ijAij⊗Fij
∑ijAijρA⊗Fij=∑ijρAAij⊗Fij,
因此,AijρA=ρAAij对任意(i,j)都成立.
证毕.
在上述过程中可以发现, 局部算子Aij和ρA的交换性决定了一个态是否是懒态. 利用这一点可以给出另一个懒态的等价刻画. 在这之前, 我们回顾一下非交换性度量的定义.
令X和Y是希尔伯特空间上任意给定的两个算子. 那么[X,Y]=XY-YX=0当且仅当‖[X,Y]‖=0, 其中‖·‖为算子空间上定义的任意范数. 也就是说[X,Y]≠0蕴含着X和Y的非交换性. 一般的, ‖[X,Y]‖度量了X和Y的非交换性. 对一族算子Γ={Al∶1≤i≤n}的非交换性的总和可以定义为
N(Γ)∶=∑i L{ρAB}∶=∑ij‖[Aij,ρA]‖. 借助这个定义, 很容易得到下面的推论. 推论1 对于任意作用在空间HA⊗HB上的量子态ρAB=∑ijAij⊗Fij,ρAB是懒态当且仅当L{ρAB}=0. 量子相干是量子资源理论中的一个重要概念, 近年来引起了很多学者的关注, 取得了一些相应的成果. Baumgratz等[18-19]提出了一种度量相干性的框架, 在这个框架下, 提出了l1相干度量, 相对熵相干度量, 鲁棒相干度量等度量方法. Hu M L等[20]定义了两个量子态的相对相干性(RQC). 考虑同一个希尔伯特空间里的两个量子态ρ和σ, 当σ是非退化的, 且其特征向量[1]={|ψi〉}, i.e.σ=∑1εi|ψi〉〈ψi|, 其中εi为相应的特征值. 定义ρ相对于σ的相对量子相干性为 C(ρ,σ)=C[1](ρ), 式中:C[1](ρ)为在参考基[1]下的任意一量子相干度量. 当σ是退化的时, [1]不是唯一确定的. 通过对σ的所有可能特征分解得到的相干度量取上界定义了RQC为 C(ρ,σ)=sup[1]C[1](ρ). 在本文中, 定义下相对相干度量(sub-RQC)为 因此,Cl1(ρ,σ)=inf{u∶uσ=σu}Cl1(ρ,uβ0). 证明令f(u)=Cl1(ρ,β)=Cl1(ρ,uβ0)=Cl1(uρu†,β0), 显然这是一个连续函数. 令 Uσ={u∶uσ=σu}, 若{un}⊂Uσ且un→u, 有uσ=limunσ=limσun=σu, 因此u⊂Uσ, 即Uσ是一个紧集. 证毕. 在这种情况下, 定义Csub(ρ,σ)中的下界可以取到, 进而可以把Csub(ρ,σ)改写成 Csub(ρ,σ)=min[1]C[1](ρ)∶=Cmin(ρ,σ). 定理3 假定Hd是一个d维的可分希尔伯特空间(d≤+∞), 若A和B是Hd上的两个正规算子, 那么Csub(A,B)=0当且仅当[A,B]=0. 证明若Csub(A,B)=0, 则 A=∑iλi|ψi〉〈ψi|, 其中{|ψi〉|i是B的一组基. 由定义, 在这组基下B=∑iλi|ψi〉〈ψi|. 因此, [A,B]=0. 反之, 若[A,B]=0, 这意味着A和B可以同时对角化, i.e., 存在一组基{|ψi〉}i使得A=∑iλi|ψi〉〈ψi| 且B=∑iλi|ψi〉〈ψi|. 这样就得到Csub(A,B)=0. 证毕. 至此, 可以给出懒态的另一个刻画. 定理4 对任意给定的二体态ρAB=∑ijAij⊗Fij∈B(HA⊗HB), 下列说法等价 1)ρAB是懒态; 2) ∑Csub(Aij,ρA)=0; 3) 存在HB里的一组基{|iB〉}, 使得Aij和ρA交换对于所有的(i,j)都成立. 证明1)⟹2)由定理1,ρAB是懒态当且仅当Aij和ρA交换对所有的(i,j)都成立, 又由定理3可知Csub(Aij,ρA)=0对所有的(i,j)都成立. 近而有∑Csub(Aij,ρA)=0. 2)⟹3)由定义,Csub(*,*)≥0恒成立. 若∑Csub(Aij,ρA)=0, 则Csub(Aij,ρA)=0对所有的(i,j)都成立. 由定理3可得,Aij和ρA交换. 3)⟹1)由定理1直接可得. 利用以上定理, 我们可以研究无限维情形下懒态和Discordant态以及可分态的关系. 证明若ρAB具有如命题中的形式, 显然有ρ11≥ρ22=ρ11. 由文献[21-22]可知, 若一个两体态的算子矩阵表示中的对角算子是可比较的, 则态是可分的. 由此可知, 命题中的ρAB是可分的. 由定理1, 若ρAB是懒态, 则有ρij与ρA=TrBρAB=ρ11交换对所有的(i,j)成立, 进而ρ11和ρ12一定交换. 故若ρ11和ρ12不交换, 或者ρ12不是正规算子时,ρAB不是一个懒态. 至此, 我们知道这种类型的态是可分的非懒态. 本文给出了几种两体懒态的刻画. 相较之前的判据, 本文的刻画没有维数要求, 为一般无限维情形下懒态的研究提供了便利. 事实上, 该判据对于有限维懒态的研究也提供了新的方法. 利用这些判据, 构造了一类无限维的可分但非懒态的两体量子态. 联系量子失协, 研究了懒态和量子失协的关系. 显然懒态含有区别于纠缠和量子失协的量子关联, 本文的结论对理解一般无限维系统里的量子关联提供了一定的帮助.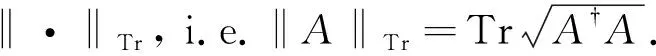
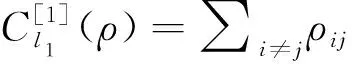
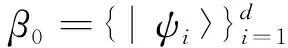
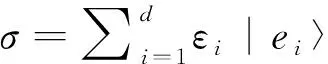
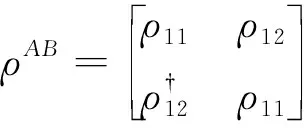
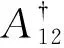
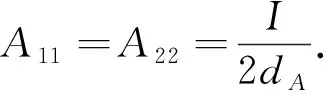
2 结 论
