■乔国颖 张文伟

直线与圆的问题中，经常出现与圆有关的轨迹问题，下面就与圆有关的轨迹问题进行归类整理，以方便同学们掌握这类题型的解题方法与技巧。

一、直接法

直接法求轨迹方程的基本步骤是∶建系设点，列出条件，代入坐标，整理化简，限制说明。

例1已知线段AB和动点C，若，求动点C的轨迹方程。

解：以AB为x轴，AB的垂直平分线为y轴，建立平面直角坐标系(图略)，则点A(-2，0)，B(2，0)。

设动点C(x，y)。

故所求动点C的轨迹方程是(x-6)2+y2=32。

评析:在平面上给定相异两点A，B，设点P在同一平面上且满足则当λ＞0且λ≠1时，点P的轨迹是一个圆。

二、几何法(定义法)

利用题中所给的几何特征判断出轨迹是一个圆，再根据圆的定义求出轨迹方程。

例2已知两定点A(1，0)，B(5，0)，过点A，B分别作两条直线l1和l2，直线l1和l2的斜率分别是k1和k2，若k1·k2=-1，求直线l1和l2的交点M的轨迹方程。

解：因为k1·k2=-1，所以l1⊥l2，可得∠AMB=90°，可知点M在以AB为直径的圆上。

因为k1·k2=-1，可知k1和k2都存在，所以M点不能和A，B两点重合，故点M的轨迹方程为(x-3)2+y2=4(y≠0)。

评析:几何法是求圆的方程的常用方法，即通过所给条件的几何特征，确定动点轨迹是一个圆，再来确定圆心和半径，从而求出圆的方程。

三、已知圆上有一动点

已知圆上有一动点，求与该动点有关的动点轨迹方程也是常见的题型，这类问题的解法相对比较固定，都是寻找所求动点坐标与圆上动点坐标之间的关系求解的。

例3已知点P(4，0)与圆O∶x2+y2=9，Q是圆O上的动点，求PQ的中点M的轨迹方程。

解：设PQ的中点M的坐标为(x，y)，动点Q(x0，y0)。

又因为点Q(x0，y0)在圆O上，所以，即得(2x-4)2+(2y)2=9，整理可得

故PQ的中点M的轨迹方程为(x-2)2

评析:已知圆上有一动点，这时要设该动点为(x0，y0)，所求轨迹的动点为(x，y)，用x，y表示出x0，y0是解题的关键。

四、已知圆上有两动点

这类问题一般是寻找这两点的弦的中点，借助圆心与弦的中点的连线和弦垂直，找出半径和弦长之间的关系。

例4已知☉O∶x2+y2=9，A(3，0)是☉O上的一个定点，B(-1，2)为☉O内的一个定点，P，Q为☉O上的两个动点。

(1)求线段AP中点M的轨迹方程。

(2)若PB⊥BQ，求线段PQ中点N的轨迹方程。

解：设中点 M(x，y)，动点P(x0，y0)

因为点P在圆x2+y2=9上，所以+=9，即得(2x-3)2+(2y)2=9，整理可得

(2)设点N(x，y)。

因为PB⊥BQ，所以△PBQ是直角三角形。

又因为N是Rt△PBQ斜边的中点，所以|PN|=|BN|。

由O为坐标原点，可知ON⊥PQ，如图1所示。

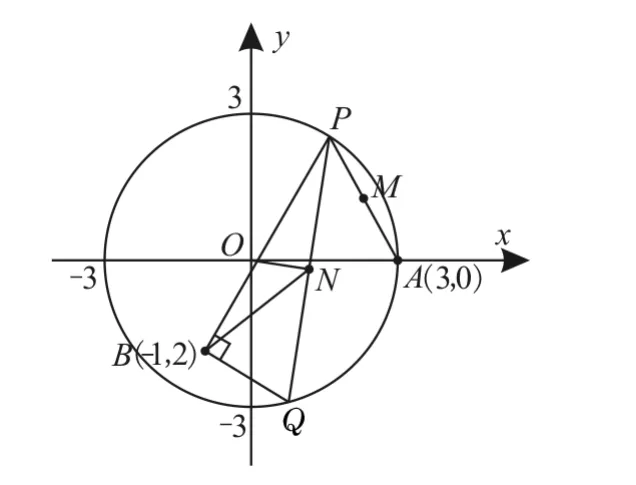
图1

评析:解答本题的关键是借助△PBQ是直角三角形，找出半径和弦长之间的关系。

编者注：本文系2018年度河南省基础教育教学研究项目《高中阶段国际班教学与管理策略研究》研究成果，项目编号∶JCJYC18250241。