一个包含数论函数φ(n)的方程的可解性
2018-11-19张四保官春梅席小忠
张四保,官春梅,席小忠
(1.喀什大学 数学与统计学院,新疆 喀什 844008;2.宜春学院 数学与计算机科学学院,江西 宜春 336000)
方程整数解的讨论是数论中的一个重要的研究内容,对这一研究内容有不少人进行过探讨[1-2]. Euler函数φ(n)是一重要的数论函数,有不少文献讨论过涉及φ(n)的方程的解问题[3-12].
笔者将讨论一个包含数论函数φ(n)的方程
φ(x-φ(φ(x)))=6
(1)
的解问题,利用初等数学的方法确定了该方程的一切解.
1 主要结果及证明
定理1方程(1)只有解x=9,11,13,17,22.
证明由文[11]的结论可知,方程φ(x)=6只有4个解x=7,9,14,18,由(1)式有
x-φ(φ(x))=7,9,14,18.
因而x≥8,φ(φ(x))必为偶数.


情况1.1.1α1=1.
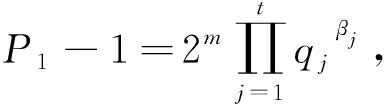
当βj=0(j=1,2,…,t)时,P1-1=2m,从而有2m-φ(2m)=6,8,因而有m=4,此时P1=17,则(1)有解x=17.
当βj(j=1,…,t)中至少有一个βj≠0时,有

或
当
时无解.当
时,有q1=5,β1=1,βj=0,j=2,…,t,从而P1-1=2×5=10,则(1)式有解x=11.
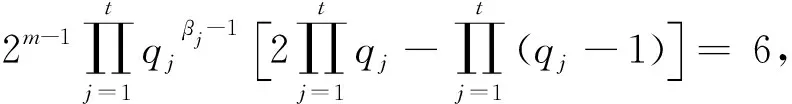
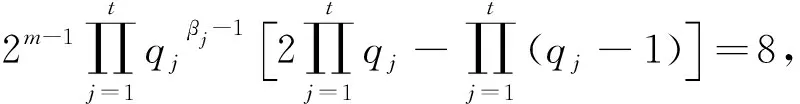
此时有t=1,β1=1,q1=7,从而P1=15,而15不是素数,则此时(1)式无解.
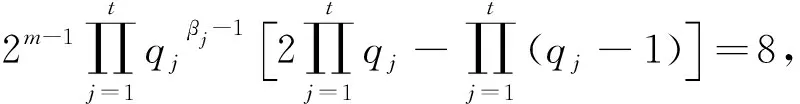
或
当
时无解.当
时,有m=2,q1=3,β1=1,βj=0,j=2,…,t,从而P1-1=22×3=12,此时(1)式有解x=13.
情况1.1.2α1≥2.
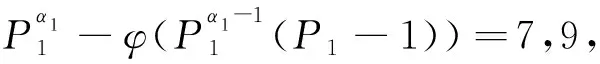
情况1.2α1≠0,α2≠0,αi=0,i=3,…,k. 此时,有
情况1.2.1α1=1,α2=1.
此时,有P1P2-φ((P1-1)(P2-1))=7,9.由于P1,P2为互异奇素数,从而有
P1P2-φ((P1-1)(P2-1))=(P1-1)(P2-1)-φ((P1-1)(P2-1))+P1+P2-1>8.
因而,当P1P2-φ((P1-1)(P2-1))=7时,(1)式无解.再讨论P1P2-φ((P1-1)(P2-1))=9的情况.由于P1,P2为互异奇素数,则P1,P2可分为2种情况:1)P1=3,P2≥5;2)P1≥5,P2≥7. 当P1=3,P2=5时,P1P2-φ((P1-1)(P2-1))=9不成立.
当P1=3,P2>5时,有
P1P2-φ((P1-1)(P2-1))=(P1-1)(P2-1)-φ((P1-1)(P2-1))+P1+P2-1>10.
当P1≥5,P2≥7时,有
P1P2-φ((P1-1)(P2-1))=(P1-1)(P2-1)-φ((P1-1)(P2-1))+P1+P2-1>12.
由此可知,当P1P2-φ((P1-1)(P2-1))=9时,(1)式无解.
情况1.2.2当α1≥2与α2≥2中至少有1个成立.效仿情况1.2.1的讨论,此时(1)式无解.
情况1.3当αi≠0,i≥3时,效仿情况1.2.1的讨论,此时(1)式无解.

情况2.1t=1.

(1)α1=1.
此时,有2P1-φ(P1-1)=14,18,因而P1≥11.当P1=11时,2P1-φ(P1-1)=18成立,则(1)式有解x=2×11=22;当P1=13时,2P1-φ(P1-1)=14,18均不成立;由于2P1-φ(P1-1)=(P1-1)-φ(P1-1)+P1+1,由当n≥2是整数,φ(n)
(2)α1≥2.

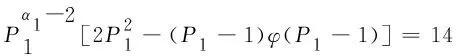
情况2.1.2α1≠0,α2≠0,αi=0,i=3,…,k.

(1)α1=1,α2=1.此时,有2P1P2-φ((P1-1)(P2-1))=14,18.
由于
2P1P2-φ((P1-1)(P2-1))=
2(P1-1)(P2-1)-φ((P1-1)(P2-1))+2P1+2P2-2=
(P1-1)(P2-1)-φ((P1-1)(P2-1))+2P1+2P2-2+(P1-1)(P2-1)>22,
则此时(1)式无解.可推知当αi(i=1,2,…,k)中满足αi≥1的个数j≥3时,(1)式无解.
(2)α1=1,α2≥2.此时,有
由于
4P2+2>(P1-1)(P2-1)2+2P1(2P2-1)+2P2(P2-2)+2>150,
则此时(1)式无解.可推知当α1≥2与α2≥2中至少有1个成立时,(1)式无解.
情况2.2t=2.

(1)α1=1.
此时,有22P1-φ(2(P1-1))=14,18.因而此时P1≥5.当P1=5时,22P1-φ(2(P1-1))=14,18均不成立;当P1=7时,22P1-φ(2(P1-1))=14,18也均不成立;由于当P1≥11时,22P1-φ(2(P1-1))=2(P1-1)-φ(2(P1-1))+2(P1-1)+4>24,即此时22P1-φ(2(P1-1))=14,18不可能成立,则此时(1)式无解.
(2)α1≥2.

(P1-1)[2(P1-1)]-(P1-1)φ(2(P1-1))+(P1-1)[2(P1-1)]+8P1-4>28,

情况2.2.2α1≠0,α2≠0,αi=0,i=3,…,k.

(1)α1=1,α2=1.
此时,有4P1P2-φ(2(P1-1)(P2-1))=14,18.由于
4P1P2-φ(2(P1-1)(P2-1))=2(P1-1)(P2-1)-φ(2(P1-1)(P2-1))+
2(P1-1)(P2-1)+4(P1+P2-1)>2(P1-1)(P2-1)+4(P1+P2-1)>44,
则此时(1)式无解.可推知当αi(i=1,2,…,k)中满足αi≥1的个数j≥3时,(1)式无解.
(2)α1=1,α2≥2.

(P2-1)[2(P1-1)(P2-1)]-(P2-1)φ(2(P1-1)(P2-1))+
则此时(1)式无解.可推知当α1≥2与α2≥2中至少有1个成立时,(1)式无解.
情况2.3t=3.
情况2.3.1α1≠0,αi=0,i=2,…,k.此时,有
(1)α1=1.
此时,有23P1-φ(4(P1-1))=14,18.当P1=3时,23P1-φ(4(P1-1))=14,18均不成立.由于23P1-φ(4(P1-1))=4(P1-1)-φ(4(P1-1))+4(P1+1)>4(P1+1),因而当P1≥5时,23P1-φ(4(P1-1))>24,从而23P1-φ(4(P1-1))=14,18也均不成立,则此时(1)式无解.
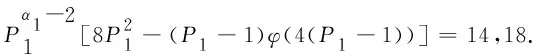
(P1-1)φ(4(P1-1))+(P1-1)[4(P1-1)]+16P1-8>56,
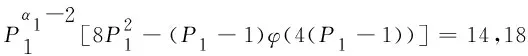
情况2.3.2α1≠0,α2≠0,αi=0,i=3,…,k.此时,有
(1)α1=1,α2=1.
此时,有8P1P2-φ(4(P1-1)(P2-1))=14,18.由于
8P1P2-φ(4(P1-1)(P2-1))=4(P1-1)(P2-1)-φ(4(P1-1)(P2-1))+
4(P1-1)(P2-1)+8(P1+P2-1)>4(P1-1)(P2-1)+8(P1+P2-1)>88,
则此时(1)式无解.可推知当αi(i=1,2,…,k)中满足αi≥1的个数j≥3时,(1)式无解.
(2)α1=1,α2≥2.此时,有
由于
4(P1-1)(P2-1)2-(P2-1)φ(4(P1-1)(P2-1))+
则此时(1)式无解.可推知当α1≥2与α2≥2中至少有1个成立时,(1)式无解.
情况2.4t=4.
情况2.4.1α1≠0,αi=0,i=2,…,k.此时,有
(1)α1=1.
此时,有24P1-φ(8(P1-1))=14,18.当24P1-φ(8(P1-1))=8P1-φ(8(P1-1))+8P1>24,则(1)式无解.
(2)α1≥2.此时,

情况2.4.2α1≠0,α2≠0,αi=0,i=3,…,k.此时,有
(1)α1=1,α2=1.此时,有
16P1P2-φ(8(P1-1)(P2-1))=14,18.
由于
16P1P2-φ(8(P1-1)(P2-1))=8P1P2-φ(8(P1-1)(P2-1))+8P1P2>120,
则(1)式无解.可推知当αi(i=1,2,…,k)中满足αi≥1的个数j≥3时,(1)式无解.
(2)α1=1,α2≥2.

则(1)式无解.可推知当α1≥2与α2≥2中至少有1个成立时,(1)式无解.
将以上各种情况的讨论进行综合,得方程(1)只有5个整数解x=9,11,13,17,22.证毕.
