付俊杰 刘功申

(上海交通大学电子信息与电气工程学院 上海 200240) (tianzhiyinyi@sjtu.edu.cn)

二分类是在不同领域的诸多应用中的一项非常常见的任务，如欺诈检测、疾病预测、风险管理、文本分类等.在这些应用中，其中一个类别的数据数量远超出另一个类别，使得传统的机器学习方法难以得到理想的结果[1].除了直接预测数据对应的分类标签，许多应用还可能关心这个预测的准确性有多少，也就是想知道数据属于某个分类的概率[2].相对直接得到分类标签，分类概率的预测往往能为人们的决策判断提供额外的帮助.比如在医疗领域，医生经常会通过声学成像得到的图像数据来判断病人是否患有某种疾病，比起直接诊断病人是否患病，能说出病人有百分之几的可能性患病将更有说服力[3].

非平衡数据分类的常用方法包括过采样/欠采样方法[4]、代价敏感学习[5]和集成学习，比如boosting方法[6].其中，采样方法比较简单且适应性较强，该方法的出发点简单清晰，既然2个类别的数据量差异悬殊，就想办法将它们拉近，然后用经典的分类算法解决问题；代价敏感学习与直接考虑数据数量的采样方法不同，它考虑的是数据分错类别时的代价，使分类器能更看重少类数据；集成学习先将原数据集划分为多个子集，然后分别对每个子集训练得到多个子分类器，最后将这些子分类器集成得到一个分类器，提高少类的分类准确性.然而到现在为止，关注分类概率预测的研究还较少.为了解决这个问题，一个自然的选择便是广义线性模型[7].众所周知，广义线性模型具有模型简单、鲁棒性强、泛用性广等优点，在不同的链接函数下，广义线性模型展现出了其良好的灵活性，更重要的是，该模型能直接给出分类的概率预测.然而，广义线性模型中通常使用的链接函数对非平衡数据的适应性不佳[8]，因为大多数链接函数的曲线形状是对称的，从而导致它们对不同的错分给予了相同的代价.因此，有研究表明，用非对称的链接函数将更有利于非平衡数据分类[9-10]，而其中一种非对称链接函数便是广义极值(generalized extreme value, GEV)分布的累积分布函数.由于形状参数ξ的存在， GEV链接函数能以不同的曲线斜率提供丰富多样的曲线类型，可以适应现实生活中的各种不同平衡度的数据.

GEV分布广泛应用于金融、气象、计算机视觉等领域.近年来，将GEV分布作为链接函数运用在线性模型中的做法受到了一定的关注：Wang等人[9]将GEV链接函数运用到B2B电子支付系统的二分类问题中，得到了很好的结果；Calabrese等人[10]则在信贷领域的稀有事件分类中运用了GEV分布，通过最大化似然概率得到了模型的解；Agarwal等人[11]更是根据GEV分布的形式求得了对应的标准优化函数，使整个问题化为凸优化问题，在精确的分类概率预测问题上给出了一种解决方案.在这些研究中所用到的数据均是非平衡数据，而且均采用了GEV链接函数，这表明GEV分布在解决非平衡数据分类问题中具有一定潜力.

1 GEV线性回归

1.1 广义线性模型与GEV分布

令y∈{0,1}表示数据的分类标签，x=(1,α1,α2,…,αd)T∈d+1表示输入的数据，给定x的条件下y的期望为

E[y|x]=P(y=1|x)=g(βTx)，

(1)

其中,β是权重参数，g的逆函数被称为链接函数.链接函数可以是任意的严格递增函数，其定义域与值域符合g-1:[0,1]→，常用的有Logit链接、Probit链接和Cloglog链接等，前两者是对称链接函数，而Cloglog链接则是非对称的.

GEV链接函数也是非对称函数，与Cloglog不同的是，GEV链接函数具有可以调节非对称程度的形状参数.当均值为0、方差为1时，GEV分布的累积分布函数为

(2)

其中(·)+表示max(0,·);ξ是形状参数，控制着函数曲线形状以及定义域.GEV链接函数和其他的链接函数有2个主要区别：1)GEV链接函数具有可调的形状参数，使得GEV链接函数可以通过改变曲线形状来适应不同的数据，尤其是具有不同非平衡程度的数据；2)GEV链接函数族中的大多数曲线都是非对称的，图1展示了在不同的形状参数下GEV分布的累积分布函数(CDF)和概率密度函数曲线(PDF).曲线的非对称性意味着GEV链接函数对不同的分类错误会给予不同的错分代价，而这正是处理非平衡数据分类问题的一个有效策略.

Fig. 1 CDF and PDF of GEV distribution with different values of ξ图1 不同ξ值的GEV分布的累积分布函数和概率密度函数

1.2 GEV线性回归

在广义线性模型框架下，为了求得权重参数β，通常会以最大化似然概率为目标.假设有n个独立同分布的数据样本，那么广义线性模型的目标优化函数即是：

(3)

但是当形状参数ξ处在特定的区间时，上面的目标优化函数并非凸函数，也即无法求得全局最优解.为了解决这个问题，Agarwal等人[11]利用组合损失函数的方法求得了GEV链接函数对应的标准损失函数，使其配对形成凸函数优化.该方法在小数据集上有较好的表现，但由于其每轮运算中都需要计算海森矩阵的逆矩阵，该方法在大数据集上有计算性能问题.

为了在保证凸函数优化的基础上进一步提升运算性能，本文运用了校准损失函数作为目标优化函数，该目标优化函数能以更通用的形式支持许多链接函数，使其能组合成为凸函数[12].校准损失函数为

l(β)=G(βTx)-yβTx，

(4)

其中，G为逆链接函数g的原函数.在这里g必须是单调递增的以保证原函数的存在以及该函数的凸性.而原函数G不必直接求出，因为在算法迭代中需要计算的是梯度和海森矩阵，它们分别是：

(5)

(6)

因为g是单调递增的，也即g′(βTx)≥0，容易证明海森矩阵是半正定的，因此最小化上面的校准损失函数可以转换成凸优化问题.

如果函数g满足利普希茨连续性，那么迭代算法的效率就能通过近似计算海森矩阵而得到提升.利普希茨连续性意味着存在一个常数L≥0，使得对于所有u，v∈，以下关系成立：

|g(u)-g(v)|≤L|u-v|，

(7)

式(7)表明函数g的斜率有最大值L.如果这个斜率最大值L能计算出来，那么我们可以简单地将其替换到g′(βTx)的位置，使得牛顿法的迭代过程简化为

βnew=βold-(LxxT)-1·(g(βTx)-y)x|β=βold.

(8)

此处用斜率最大值L替换精确的梯度，相当于在梯度更新方向正确的前提下提供了最小步长，而各维的实际更新步长仍受原始数据xxT的影响，保证了一定的参数更新效率.在替换过后，每轮的迭代计算中逆矩阵的运算与β无关，逆矩阵的计算可以放在循环开始前，这样就能大大提高计算的效率.这种利普希茨优化既保留了牛顿法中的原始数据二阶信息结构，还能像梯度下降法那样有效率地更新，继承了两者的优点.

对于GEV链接函数，其符合利普希茨连续性，斜率最大值L为

L=exp(-(1+ξ))(1+ξ)1+ξ，

(9)

其中，形状参数ξ≥-1，否则g′(βTx)会趋向无穷，有意义的L值将不存在.虽然这限制了ξ的取值，但有研究表明，ξ的取值在[-0.5,0.5]之间就能提供足够的曲线形状来使GEV链接函数具有高度的灵活性[9].

完整的算法如算法1所示.为避免过拟合，算法1中添加了L-2正则项.形状参数ξ是一个重要的参数，它直接影响模型对非平衡数据的拟合程度，所以关于它的选取方法将放到第2节单独介绍.β的初始值可以随机设为接近0的值，或通过第2节介绍的方法设置.

算法1. GEV线性回归算法.

输入：XT=(x0,x1,…,xn)，xi∈k，Y=(y1,y2,…,yn)T，yi∈{0,1}，使用概率模型选优得到GEV形状参数ξ∈[-1,+∞)，正则参数λ>0；

输出：权重参数β.

初始化：

通过式(9)计算L.

步骤1. 计算近似海森矩阵的逆矩阵Σ-1=(L·XTXn+λI)-1，设置迭代下标t=0；

步骤2. 重复步骤2.1～2.4直到β收敛：

步骤2.3.βt+1=βt-Σ-1·zt；

步骤2.4.t=t+1.

2 形状参数求取

为了能更好地发挥GEV链接函数的性能，形状参数的选取尤为重要.交叉验证可以作为一种备选方法，然而当需要选优的参数较多时，交叉验证将变得非常耗时，因此这里使用概率模型对形状参数选优.

2.1 最大化后验概率

模型主要有2个参数待求解：权重参数β和形状参数ξ.观察到实际中形状参数合适值在0附近，所以假设其服从标准正态分布，即P(ξ)=N(ξ|0,1).而权重参数各维数值不应过大，假设其各维度也服从标准正态分布，即P(βi)=N(βi|0,1)，并假设权重参数与形状参数互相独立.因此整个模型的后验概率为

P(β,ξ|X,Y)∝P(Y|X,β,ξ)·P(β)·P(ξ)，

(10)

其中P(Y|X,β,ξ)是模型的似然概率，其单个yi在广义线性模型框架下服从伯努利分布.对式(10)取对数后有：

(11)

Wang等人[9]在他们的研究中也用了类似的模型并通过最大化后验概率(MAP)求得解，所不同的是他们还研究了其他的先验概率分布，并且求解算法用的是马尔可夫链蒙特卡罗方法.本文运用MAP方法是为了根据输入数据自动选择较优的形状参数ξ.因此，模型中对权重参数β的求解不是必须的，权重参数是利用本文提出的GEV线性回归算法来求解的.考虑到这一步骤的主要目标，本文对MAP的求解将采用迭代类算法，如牛顿法或梯度下降法，在每轮迭代中轮流更新权重参数和形状参数.MAP目标优化函数分别对β和ξ求一阶偏导数有：

(12)

(13)

其中,ai=1+ξηi.有了一阶偏导数后就可以采用梯度下降法求取MAP目标优化函数的最大值，或继续计算各自的二阶偏导数利用牛顿法更新参数.得益于ξ的低维度，只需要很少的迭代次数就可以使形状参数收敛到一个可接受的范围.算法运行完后的副产物β参数可以看作是寻优过程的“中途解”，将之用作GEV线性回归算法的初始值，可以进一步减少让β参数收敛所需的迭代次数，改进回归算法的效率.

2.2 贝叶斯分析

在MAP概率模型中，目标优化函数是后验概率，我们假设GEV线性回归算法中的形状参数ξ和权重参数β都服从于一个确定的标准正态分布，这有时会变得不合适.贝叶斯分析中，我们依旧假设形状参数ξ和权重参数β都服从正态分布，但是正态分布的2个关键参数——均值和方差，可以是未知的.为了方便计算，假设P(ξ|μξ)=N(ξ|μξ,1),P(β|μβ)=N(β|μβ,I),其中μξ和μβ分别是ξ的均值和β的均值，I是单位矩阵.通过证据近似法最大化边缘似然概率P(Y|μξ,μβ)可以得到ξ和β.在计算中，ξ和β可以看作是隐变量，通过EM算法迭代求解.M步骤中需要最大化的目标函数Q为

Q(μξ,μβ|μξ,μβ)=

(14)

然而式(14)涉及对GEV分布的积分，直接计算很困难，所以这里通过Metropolis-Hastings采样方法对此积分进行近似计算:

(15)

(16)

得到求和形式的函数Q后即可通过求导计算更新后的μξ和μβ,最优形状参数ξ直接取μξ的均值即可.像MAP方法一样，副产物μβ可以用于GEV线性回归算法的初始化中.

3 实 验

本节实验主要分为3个部分：1)通过人工数据集验证形状参数求取方法的准确性；2)在真实数据集上横向对比本文算法和其他线性回归算法，在分类准确性和概率预测准确性上分别做出评价；3)对本文算法的运行效率进行实验.

3.1 数据集与评价标准

人工数据集方面，数据维度为2维，采用互相独立的标准正态分布随机生成数据点xi，并固定权重参数β=(1,1)T，通过GEV逆链接函数生成分类概率值yi.本次实验用的生成数据集使用了3个形状参数值ξ，分别是-0.1，0.2，0.5；生成数据集的大小也有3种：100个、500个和1 000个，共9个生成数据集.真实数据集来源于Keel数据仓库中的非平衡数据集[13].本次实验根据数据所属领域以及非平衡程度，从中挑出了17个真实数据集，它们均来自不同领域并具有不同的非平衡程度(IR)，IR等于负类数量正类数量.数据集名称、数据量、特征维度数以及非平衡程度如表1所示.

在分类准确性评价上，本文采用AUC指标作为评价标准.AUC是公认的对非平衡数据分类评价较为合适的指标，AUC越大表示分类器的性能越好[14].为了评价算法的概率预测准确性，采用Brier指标和标度损失来评价分类结果，它们的定义如下：

Table 1 Description of Datasets Used in Our Experiments表1 真实数据集概况

3.2 形状参数求取实验

在形状参数寻优实验中，测试的方法是最大化后验概率和贝叶斯分析.2种方法的初始ξ值均为0.1.图2展示最大化后验概率在9组生成数据集下ξ值随迭代次数的变化图像.

从图2可以看到，9组生成数据集下的ξ值在最大化后验概率方法下基本收敛，且ξ值变化的方向与其正确值一致，这说明最大化后验概率方法对于形状参数寻优的有效性.最终搜寻到的ξ值如表2所示.

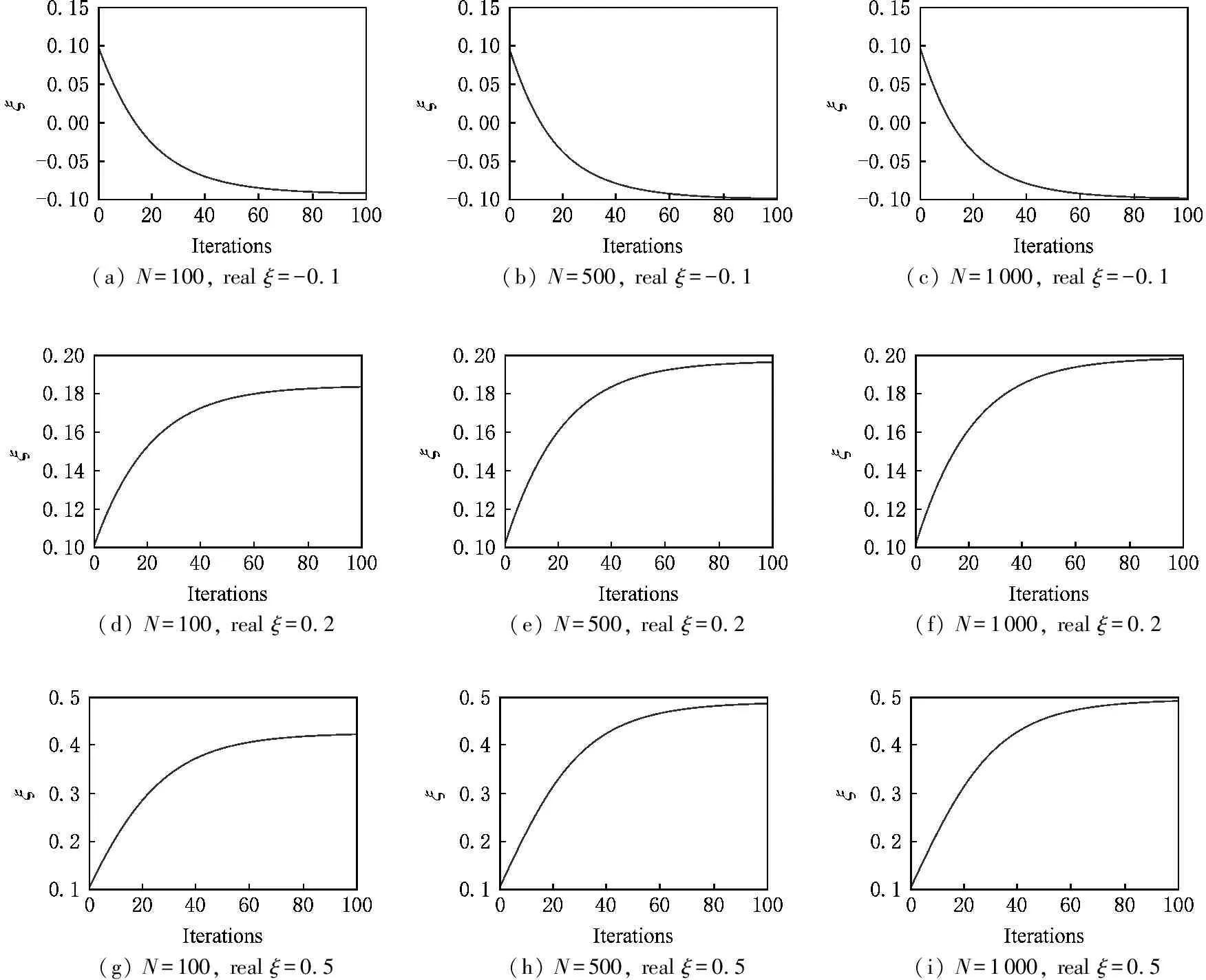
(a) N=100, real ξ=-0.1 (b) N=500, real ξ=-0.1 (c) N=1000, real ξ=-0.1 (d) N=100, real ξ=0.2 (e) N=500, real ξ=0.2 (f) N=1000, real ξ=0.2 (g) N=100, real ξ=0.5 (h) N=500, real ξ=0.5 (i) N=1000, real ξ=0.5

Fig. 2 Convergence of ξ under MAP method图2 最大化后验概率方法下ξ值的收敛情况

Table 2 Estimation of the Shape Parameter Under MAP Method

观察表2可知，最大化后验概率方法最终搜寻到的ξ值基本正确，但当数据量为100时ξ值离正确值最远，数据量为1 000时最近.这表明最大化后验概率的参数寻优性能随数据量的增大而提高，数据量过少时ξ值有较大偏差，但仍在可以接受的范围内.

接下来是贝叶斯分析对参数寻优的实验.实验中，EM算法的迭代次数为10，每次迭代调用MH算法采样的样本数量为10 000～20 000均匀递增.图3为贝叶斯分析下对数似然概率值以及ξ值的收敛过程.

从图3可以看到，采样方法下的参数收敛过程并不平滑，细微的抖动情况非常多.ξ值基本朝正确的方向收敛，表示目标函数优化正确.贝叶斯分析方法最终搜寻到的ξ值如表3所示.

(a) Log Probability when N=100, real ξ=-0.1 (b) Log Probability when N=500, real ξ=-0.1 (c) Log Probability when N=1000, real ξ=-0.1

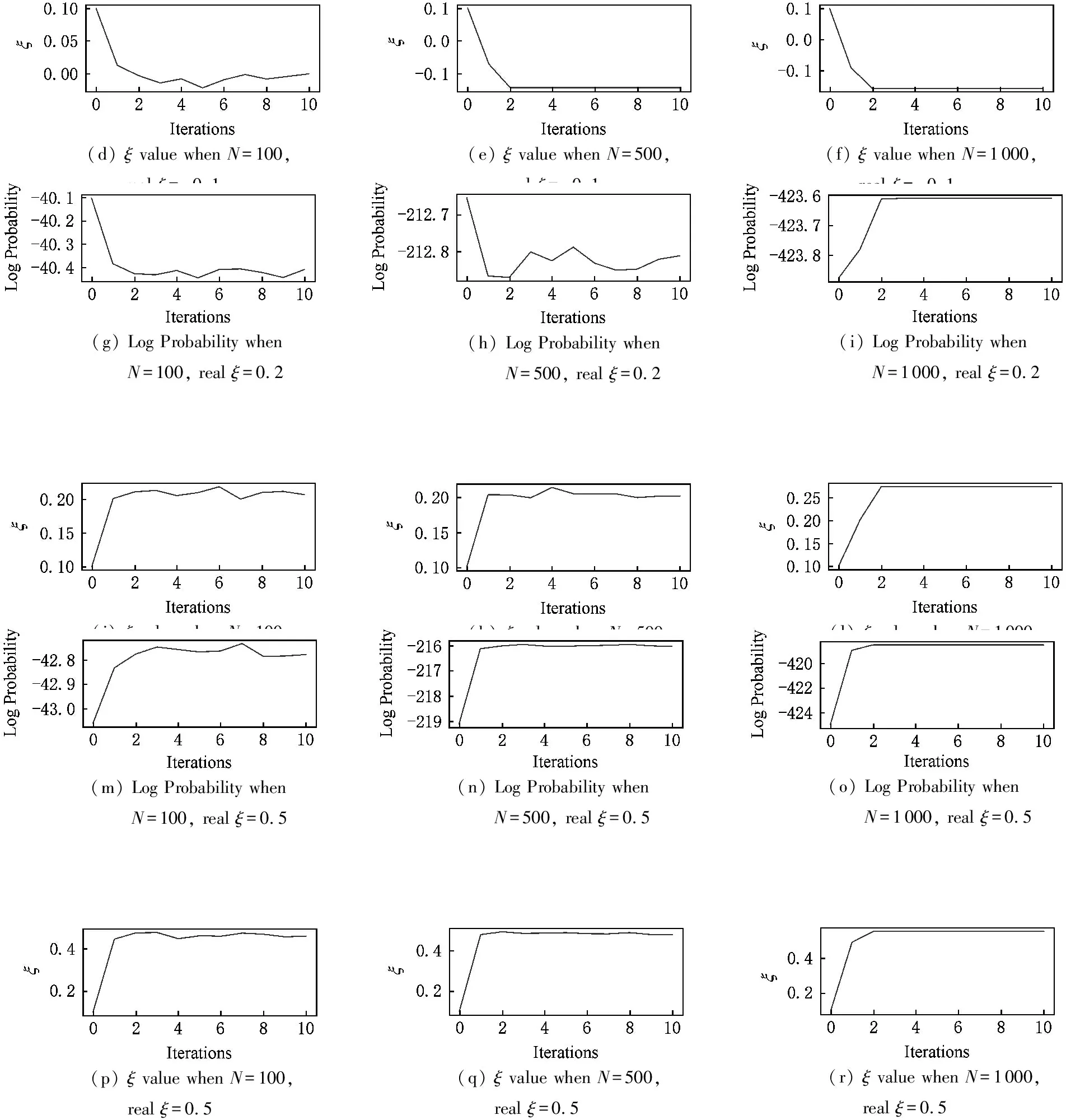
(d) ξ value when N=100, real ξ=-0.1(e) ξ value when N=500, real ξ=-0.1(f) ξ value when N=1000, real ξ=-0.1(g) Log Probability when N=100, real ξ=0.2(j) ξ value when N=100, real ξ=0.2(h) Log Probability when N=500, real ξ=0.2(k) ξ value when N=500, real ξ=0.2(i) Log Probability when N=1000, real ξ=0.2(l) ξ value when N=1000, real ξ=0.2(m) Log Probability when N=100, real ξ=0.5(p) ξ value when N=100, real ξ=0.5(n) Log Probability when N=500, real ξ=0.5(q) ξ value when N=500, real ξ=0.5(o) Log Probability when N=1000, real ξ=0.5(r) ξ value when N=1000, real ξ=0.5

Fig. 3 Convergence of ξ and Log Likelihood under Bayesian analysis图3 贝叶斯分析方法下的ξ值和对数似然的收敛情况

Table 3 Estimation of the Shape Parameter Under Bayesian Analysis

从最终参数寻优结果来看，数据量为100时贝叶斯分析有一个彻底错误的数据，其他结果基本正确.还可以发现数据量的多少对结果的影响没有像最大化后验概率方法那样明显，数据量为500和1 000的参数寻优结果相差并不大.

3.3 对比实验

本节实验测试GEV线性回归算法在真实数据集上的表现，包括分类准确性和概率预测准确性.

对比的其他算法为Logit回归、Probit回归和Cloglog回归算法，还包括用SMOTE技术预处理数据的版本[16]，其中用SMOTE技术预处理后数据的非平衡度大约为1.数据集随机划分为70%的训练集和30%的测试集，实验结果取10次分类的均值.本文的GEV线性回归算法使用最大化后验概率方法来选取最优的形状参数ξ，形状参数寻优的迭代次数和线性回归的迭代次数分别为20次和100次.各算法在各数据集上的AUC指标、Brier指标和标度损失分别如表4～6所示，其中最优结果用粗体表示.所使用的统计显著性检验方法为双侧Wilcoxon检验，结果后的符号“*”和“**”分别表示在置信水平为90%和95%时该结果与该行中的最好结果相比在统计上是显著的.

在分类准确性上，GEV线性回归算法在大部分真实数据集上都能取得较好的分类结果，而由Logit和Probit链接函数这2种对称函数构成的回归算法在SMOTE预处理技术的帮助下也能得到部分最优结果，这从另一个角度说明它们的对称性只适用于平衡数据.在概率预测准确性上，GEV线性回归算法给出了大部分的最优结果，表明其在分类的概率预测值上能提供更准确的结果.其他3种回归算法在SMOTE预处理下并没有给出更好的结果，很多情况下反而更糟糕，这可能是因为SMOTE预处理下新生成的人为数据扰乱了概率值的准确预测.

Table 4 Results of Classification Accuracy on the Datasets in Terms of AUC Score表4 以AUC指标评价分类准确度的结果

Notes： The superscripts “*” and “**” indicate statistical significance of the best method in that row with respect to other methods on the 90% and 95% confidence interval respectively.

Table 5 Results of Class Probability Estimation on the Datasets in Terms of Brier Score表5 以Brier指标评价概率预测准确度的结果

Continued (Table 5)

Notes： The superscripts “*” and “**” indicate statistical significance of the best method in that row with respect to other methods on the 90% and 95% confidence interval respectively.

Table 6 Results of Class Probability Estimation on the Datasets in Terms of Calibration Loss表6 以标度损失评价概率预测准确度的结果

Notes： The superscripts “*” and “**” indicate statistical significance of the best method in that row with respect to other methods on the 90% and 95% confidence interval respectively.

3.4 运行效率实验

本节实验内容主要有2部分:1)观察在3种最优化方法(利普希茨优化(Lipschitz)、梯度下降法(Gradient)、牛顿法(Hessian))下目标优化函数的收敛速度，也即其值随迭代次数的增多而下降的趋势;2)简单测量3种最优化方法的运行时间.其中梯度下降法还混合采用了二分线搜索方法加快步长参数的搜索.

1) 对3个最优化方法的收敛速度的实验.在作图观察时，由于校准损失函数无法求值，所以用对数损失函数代替.这里选取了6个具有代表性的真实数据集，各取了前10轮迭代，结果如图4所示:

Fig. 4 Comparison of convergence rate of three optimization methods图4 3种最优化方法的收敛速度比较

从图4可以看出，随着算法不断迭代，3种最优化方法都能使对数损失函数变小，其中梯度下降法减小的速度最慢，利普希茨优化次之，牛顿法最快，这符合预期.另外还可以看到，利普希茨优化的收敛速度其实与牛顿法非常接近，两曲线几乎重合.这得益于利普希茨优化在保留了数据的二阶结构的同时用常数近似了海森矩阵，取得了与牛顿法差不多的效率.

2) 方法运行时间的实验.3种最优化方法在每个真实数据集上都运行了10遍，每种最优化方法也都跑满了100次迭代.最终结果如表7所示，用时最短的结果已加粗显示.显然，利普希茨优化取得了所有真实数据集的最优结果，这得益于其将海森矩阵的逆矩阵计算提前到了迭代之前，大大减少了每轮迭代的运算量.可以看到，本文使用的利普希茨优化在算法运行效率上有显著的提高.

Table 7 Comparison of Average Running Time of Three Optimization Methods

4 小 结

为了解决非平衡数据分类的概率预测问题，本文提出了GEV分布作为链接函数与校准损失函数相结合的算法.具有形状参数的GEV分布可以提供高度灵活的曲线形状来适应各种非平衡数据，并且目标优化函数是一个凸函数，算法确保了全局最优解的存在.利用GEV逆链接函数的利普希茨连续性，本文提出的GEV线性回归算法在运行效率上得到了显著改善.此外，本文还提出了2个基于概率的模型来求取形状参数，并利用人工数据集上的实验证实了2个模型对形状参数求取的有效性.

在真实数据集上的实验显示了本文算法有着较高的概率预测准确性以及良好的分类性能.此外，在与其他优化方法的比较中，本文所提优化方法表现出很高的计算效率.未来的工作包括继续研究更健壮的形状参数求取方法以及对高维数据的实验.