徐 姜

在微分动力系统中，研究生化系统极限环的存在唯一性是十分重要的问题.1984年，廖山涛证明了三维离散系统和四维无奇点常微系统稳定推测.1997年，吴云华用数学的方法证明了系统正奇点存在唯一的充要性条件.2001年，孙宝法给出了二次系统恰有一个无穷远奇点的充要条件.可逆饱和的生化系统是相对比较难的研究对象.本文应用了微分动力学理论在对一类可逆多分子饱和模型进行研究，其模型如下.

1 平衡点的分析

由于系统（1）具有一定的生态意义，所以讨论区域为G={(x,y)|x≥0,y≥0}.经过计算得到，当b≤a时，系统（1）无正奇点，这种情况得出系统（1）在G内无极限环.当b＞a时，系统（1）存在唯一正奇点M(A,B)，其中，

对系统（1）作变换

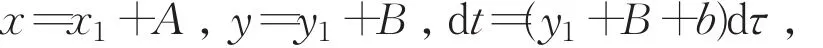
经过变换，仍以x,y代替x1,y1得到该系统的一阶线性近似方程

由此可以判定正奇点M(A,B)为非鞍初等奇点.系统（2）在(0,0)处的特征方程是

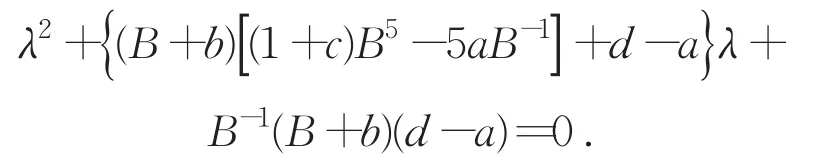
记p=(B+b)[naB-1-(1+c)B5-(1+c)B5]+a-d，则当p＞0时，M为不稳定的焦点或结点；当p＜0时，M为稳定的焦点或结点；当p=0时，M为一阶稳定的细焦点.

2 极限环的存在唯一性

定理1 当d＞a且p＞0时，系统（1）在G内奇点M(A,B)的外围至少存在一个稳定的极限环.

证明 先构造环域，当P＞0时，系统（1）的正奇点M为不稳定的焦点或结点，根据环域定理，要构造一条外境界线，让它包围正奇点M，这样系统（1）的轨线与外境界线相交时，当变量t增大时，它都是从外入内.作等倾线，如图1所示.

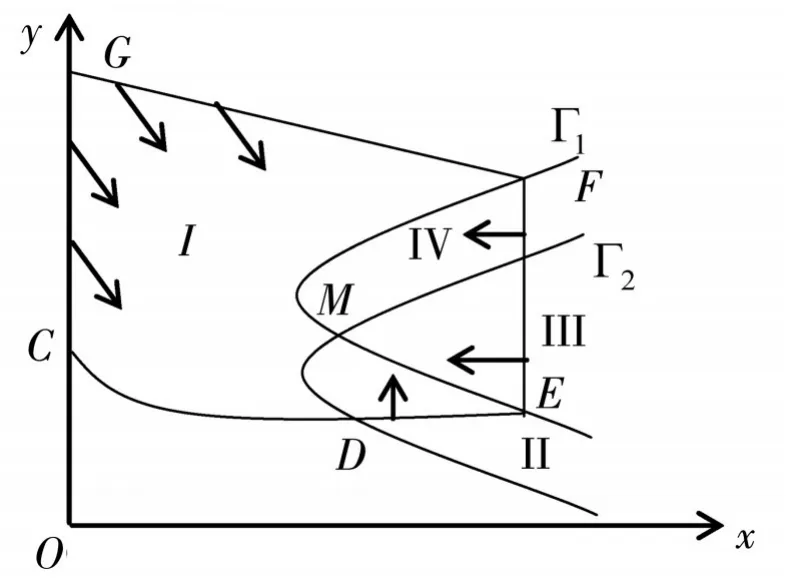
图1 轨线示意图

Γ1:a-xy5+cy=0，Γ2:xy5-cy6-dy/(y+6)=0，如图1，G被Γ1和Γ2分为4个区域，其向量场为（I）

由向量场理论以及解对初值的连续依赖性可知，有点C(0,yc)存在，当经过点C的正半轨线一定与Γ2相交于点D(xd,yd)，过点D作线段DE，交Γ1于点E，它平行于x轴.

在DE上，再过E作线段EF，交Γ1于点F(xF,yF)，它平行于y轴，且yF＞B，在EF上.过点F作直线L=x+y-(xF+yF)=0，交y轴于点G，则=-(d-a)(y-B)/(y+b)＜0(y＞yF＞B)，在GC上.则Γ=CDEFGC为封闭曲线，它就成为一条围绕M的外境界线，且系统（1）的轨线与外境界线相交时，当变量t增大时，它都是从外入内的.由环域原理知，系统（1）在Ω内至少存在一个稳定的极限环.

3 极限环的不存在性

为了讨论系统（1）的极限环的不存在性，将系统（1）化为Lienard系统.对系统（1）作变换.

u=y-B,v=x+y-(A+B),dτ=(u+B)5dt，仍记τ为t，则系统（1）化为Lienard型方程.

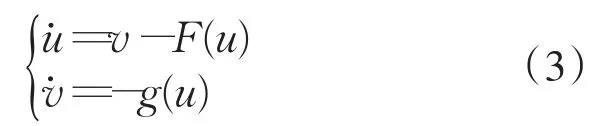
其中，-B＜u＜+∞，-(A+B)＜v＜+∞，F(u)=

系统（1）的奇点M(A,B)对应于（3）的奇点O(0,0)，故以下仅在区域 Ω={(u,v)|u＞-B,v＞-A-B}上对系统（3）讨论.

对系统（3）作菲里波夫变换Z=G(u)=分别表示Z=G(u)在u＞0及 -B＜u＜0上 的 反 函 数 ，则 有ui(0)=0,(i=1,2)，记Fi(Z)=F(ui(Z)),(i=1,2).

引理 1 若d＞a，且p＜0,则F1(Z)＞F2(Z)(Z＞0).

定理2 若d＞a，且p＜0,，则系统（1）在Ω区域内不存在极限环.

证明 系统（3）的轨线L=L1+L2也是微分方程的积分曲线，现分别在u＜0(u＞0)上对该式作变换u=u1(Z),(u=u2(Z))，则有

由引理知，F1(Z)＞F2(Z)(Z＞0)，又F1(0)=F2(0)=0.则，在 (v,Z)平面上，由v负半轴上同一点出发的两个方程（4）和（5）的积分曲线在Z≥0半平面上是没有交点的，这就是说在(u,v)平面上时，系统（3）一定没有闭轨线，所以系统（1）不存在极限环.

4 结论

本文通过常微分方程的定性理论，研究了一类可逆饱和生化系统的平衡点和极限环存在、唯一及不存在的条件.当条件更复杂时，研究起来更加困难.